Урок 80 Неравенства с двумя переменными и их системы

Содержание

1. Урок 80 Неравенства с двумя переменными и их системы
2. Неравенства 3х – 4у  0; и
3. Является ли пара чисел (-2; 3) решением неравенства:Не являетсяЯвляется
4. Решением неравенства называется упорядоченная пара действительных чисел
5. Неравенства с двумя переменными имеют вид:Множество решения
6. Множества решения неравенства ху F(x,y)≤0хуF(x,y) ≥ 0
7. Множества решения неравенстваF(x,у)>0F(x,у)
8. Правило пробной точкиПостроить F(x;y)=0 Взяв из
9. Линейным неравенством с двумя переменными называетсянеравенство вида
10. Решить графически неравенство:Строим сплошными линиями графики:-1-10x1-2y-2221
11. Определим знак неравенства в каждой из областей -1-10x1-2y-2221
12. Решение неравенства- множество точек, из областей , содержащих знак плюс и решения уравнения -1-10x1-2y-222134-+1+2-7+6-5+
13. Решаем вместе№ 1. Задайте неравенством и изобразите
14. Домашнее задание
15. Скачать презентанцию

Неравенства 3х – 4у  0; и являются неравенствами с двумя переменными х и у.Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное числовое неравенство.При х =

Главная
Разное
Урок 80 Неравенства с двумя переменными и их системы

Слайды и текст этой презентации

Слайд 1Урок 80
Неравенства
с двумя переменными
и их системы

Слайд 2Неравенства 3х – 4у  0;

и
являются неравенствами с

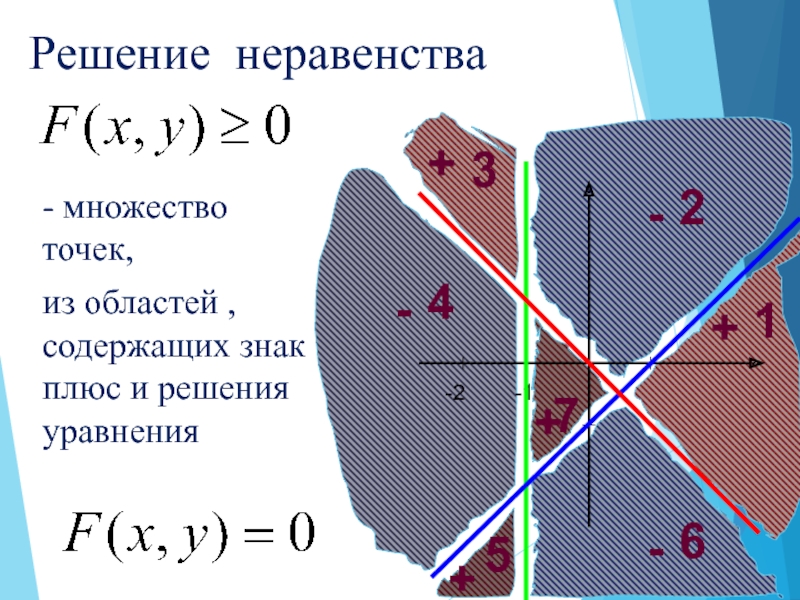
двумя
переменными х и у.
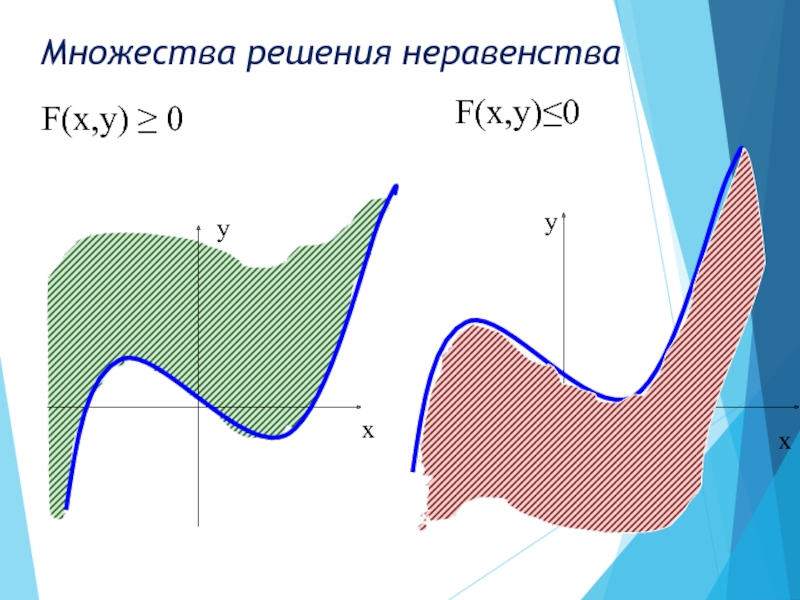
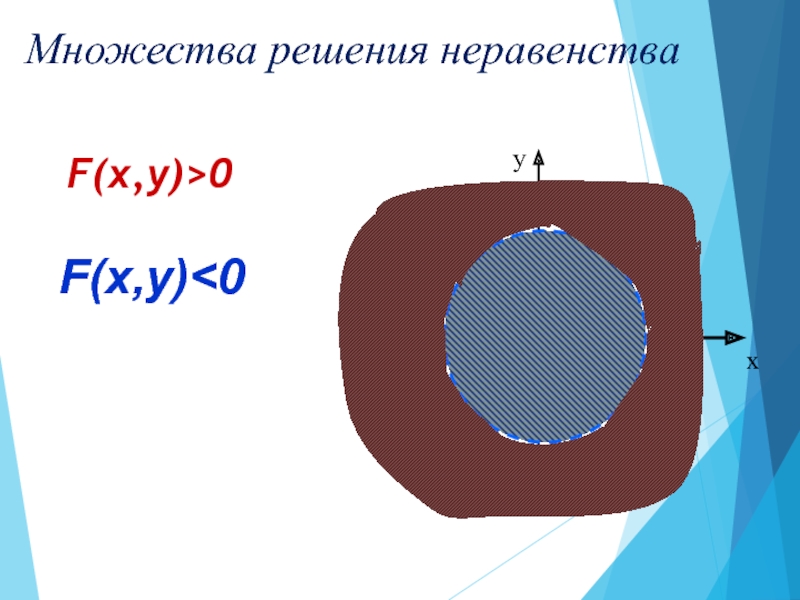
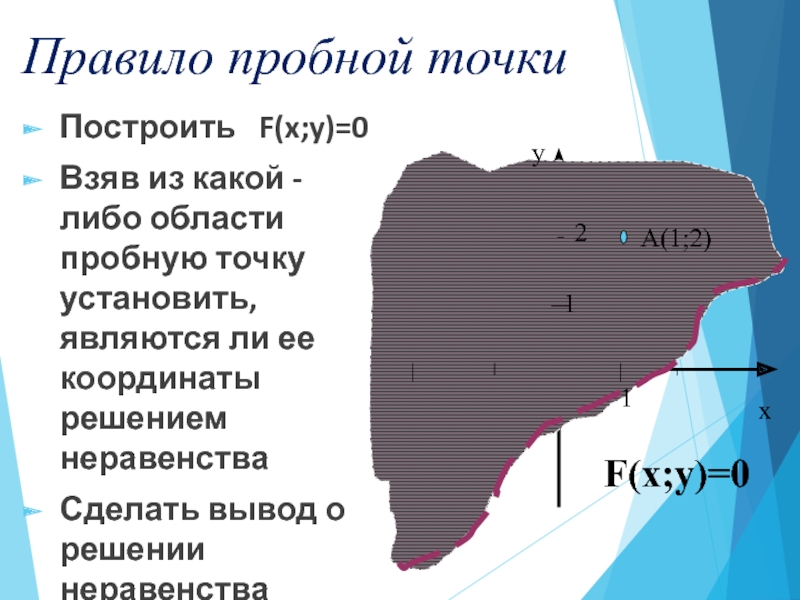
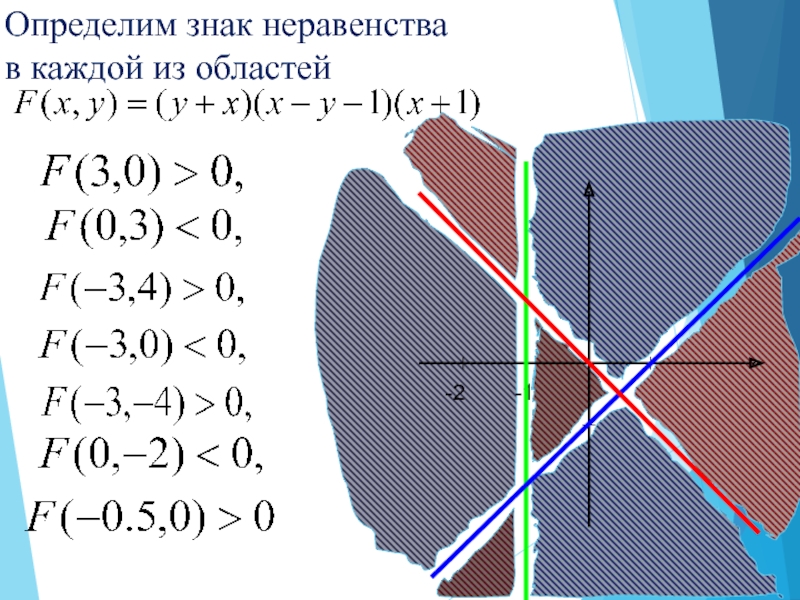
Решением неравенства с двумя переменными
называется

пара значений переменных,
обращающая его в верное числовое неравенство.

При х = 5 и у = 3 неравенство 3х - 4у  0 обращается в верное
числовое неравенство 3  0.

Пара чисел (5;3) является решением данного неравенства.

Пара чисел (3;5) не является его решением.

Неравенства 3х – 4у  0; и являются неравенствами с двумя переменными х и у.Решением неравенства с

Слайд 3Является ли пара чисел (-2; 3) решением неравенства:
Не является
Является

Слайд 4Решением неравенства называется упорядоченная пара действительных чисел

, обращающая это неравенство в верное

числовое неравенство.
Графически это соответствует заданию точки координатной плоскости.
Решить неравенство - значит найти множество его решений

Решением неравенства называется упорядоченная пара действительных чисел , обращающая это

Слайд 5Неравенства с двумя переменными имеют вид:
Множество решения неравенства - совокупность

всех точек координатной плоскости, удовлетворяющих заданному неравенству.

Неравенства с двумя переменными имеют вид:Множество решения неравенства - совокупность всех точек координатной плоскости, удовлетворяющих заданному неравенству.

Слайд 6Множества решения неравенства

х
у

F(x,y)≤0
х
у
F(x,y) ≥ 0

Слайд 7Множества решения неравенства
F(x,у)>0
F(x,у)

Слайд 8Правило пробной точки
Построить F(x;y)=0
Взяв из какой - либо

области пробную точку установить, являются ли ее координаты решением неравенства
Сделать

вывод о решении неравенства

А(1;2)

F(x;y)=0

Слайд 9 Линейным неравенством с двумя переменными называется
неравенство вида
ax + bx

+c 0 или ax + bx +c< 0,
где х

и у - переменные, a, b и c – некоторые числа,
причём хотя бы одно из чисел a и b не равно нулю.

Линейным неравенством с двумя переменными называетсянеравенство вида ax + bx +c 0 или ax + bx +c<

Слайд 10Решить графически неравенство:
Строим сплошными линиями графики:

-1
-1
0
x
1
-2
y
-2
2
2
1

Слайд 11Определим знак неравенства в каждой из областей
-1
-1
0
x
1
-2
y
-2
2
2
1

Слайд 12Решение неравенства
- множество точек,
из областей , содержащих знак плюс

и решения уравнения

-1
-1
0
x
1
-2
y
-2
2
2
1
3
4
-
+
1
+
2
-
7
+
6
-
5
+

Слайд 13Решаем вместе
№ 1. Задайте неравенством и изобразите на координатной плоскости

множество точек, у которых:
а) абсцисса больше ординаты;
б) сумма абсциссы и

ординаты больше их удвоенной разности.

№2. Задайте неравенством открытую полуплоскость, расположенную выше прямой
АВ, проходящей через точки А(1;4) и В(3;5).
Ответ: у  0,5х +3,5
№ 3. При каких значениях b множество решений неравенства 3х – bу + 7 0 представляет собой открытую полуплоскость, расположенную выше прямой 3х – bу + 7 = 0.
Ответ: b  0.

Решаем вместе№ 1. Задайте неравенством и изобразите на координатной плоскости множество точек, у которых:а) абсцисса больше ординаты;б)

Слайд 14Домашнее задание

Скачать презентацию