Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Усеченный конус
Содержание
- 1. Усеченный конус
- 2. Усеченным конусом называется часть полного
- 3. Образующей усеченного конуса называется часть
- 4. Пусть в конусе, высота которого
- 5. Усеченный конус можно рассматривать как
- 6. Пусть дан усеченный конус, радиусы оснований и высота которого известны. Найдите образующую усеченного конуса.8?
- 7. Прямая, соединяющая центры оснований, называется
- 8. Найдите площадь осевого сечения, если известны радиус нижнего основания, высота и образующая.36?
- 9. Боковая поверхность усеченного конуса. Площадь боковой поверхности
- 10. Площадь боковой поверхности усеченного конуса
- 11. Усеченный конус получен от вращения
- 12. Задача.Радиус меньшего основания усеченного конуса равен 5,
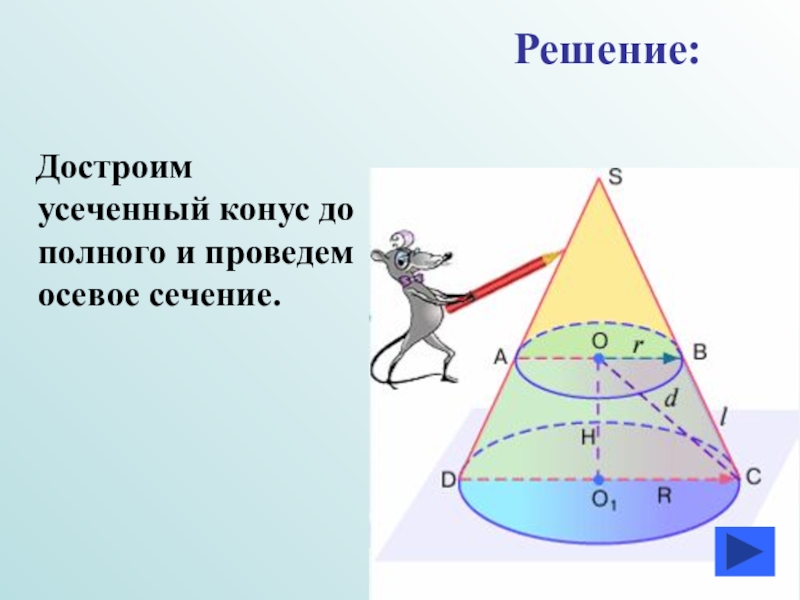
- 13. Достроим усеченный конус до полного и проведем осевое сечение.Решение:
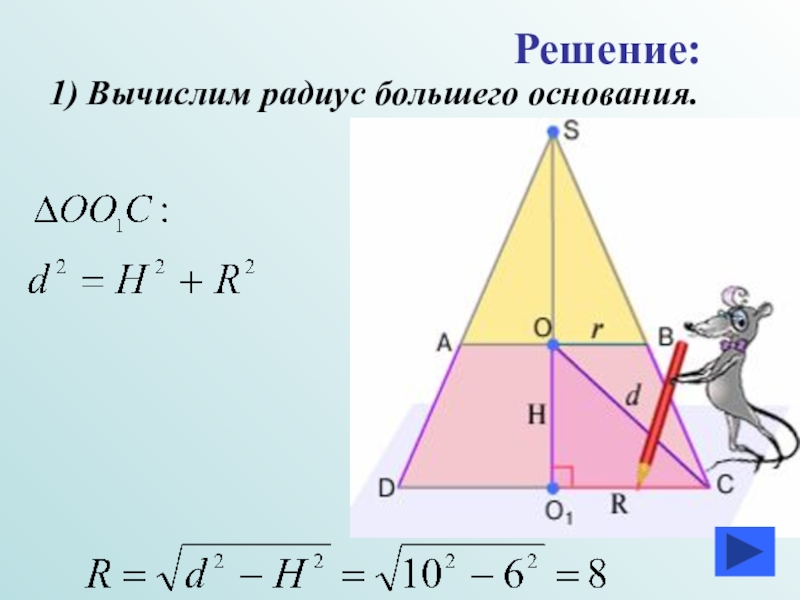
- 14. 1) Вычислим радиус большего основания.Решение:
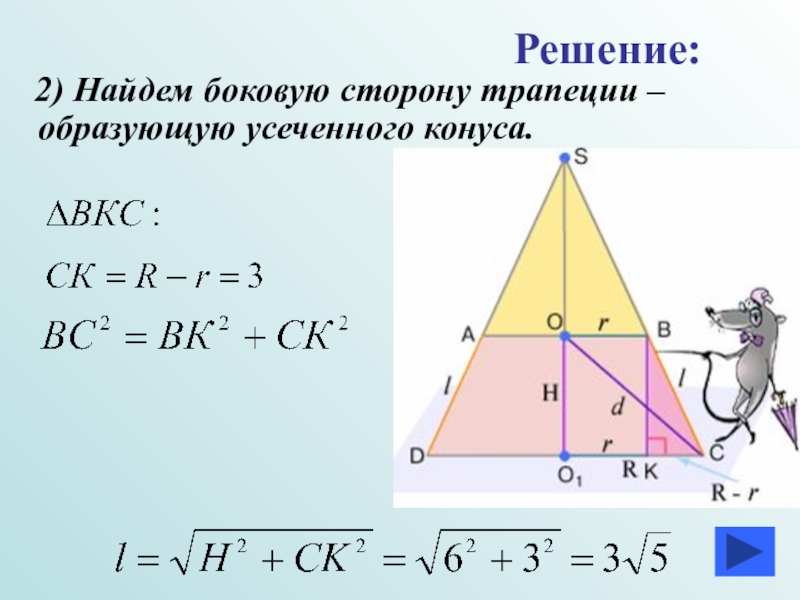
- 15. 2) Найдем боковую сторону трапеции –образующую усеченного конуса.Решение:
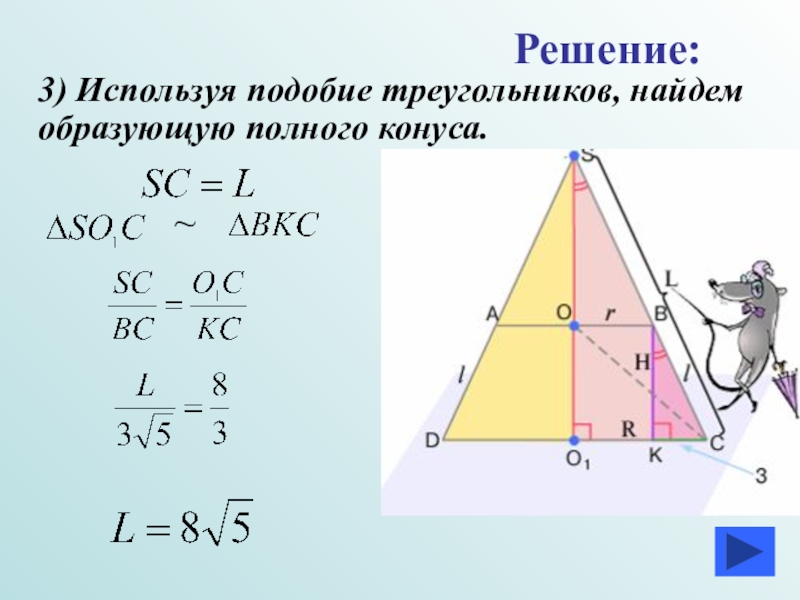
- 16. 3) Используя подобие треугольников, найдем образующую полного конуса.Решение:~
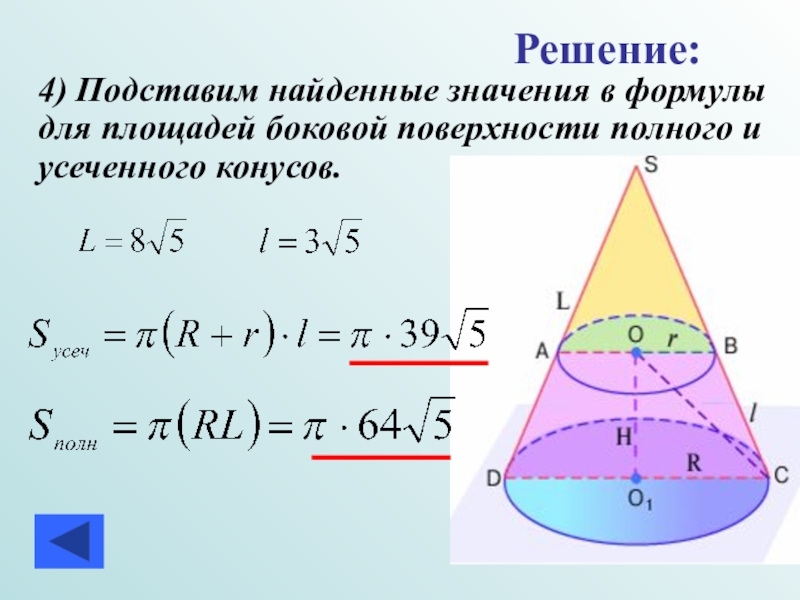
- 17. 4) Подставим найденные значения в формулы для площадей боковой поверхности полного и усеченного конусов.Решение:
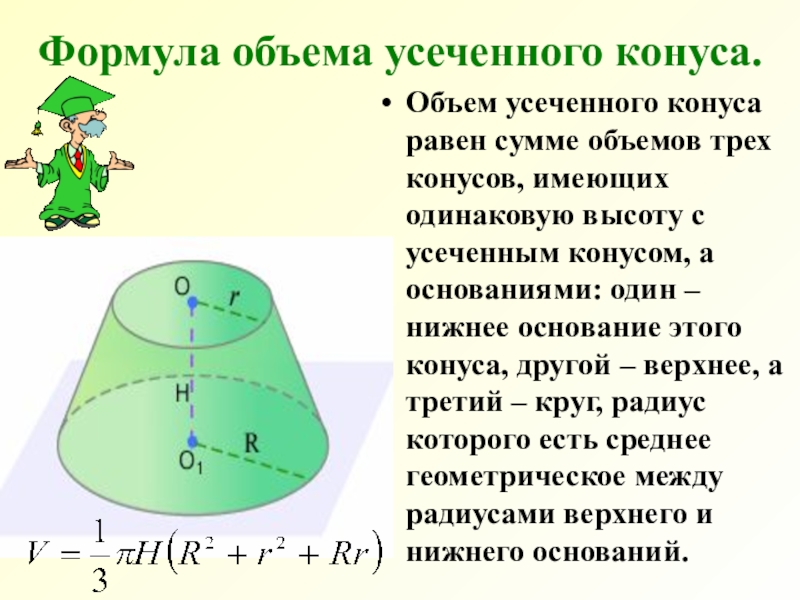
- 18. Формула объема усеченного конуса.Объем усеченного конуса равен
- 19. Поместим на верхнем основании усеченного
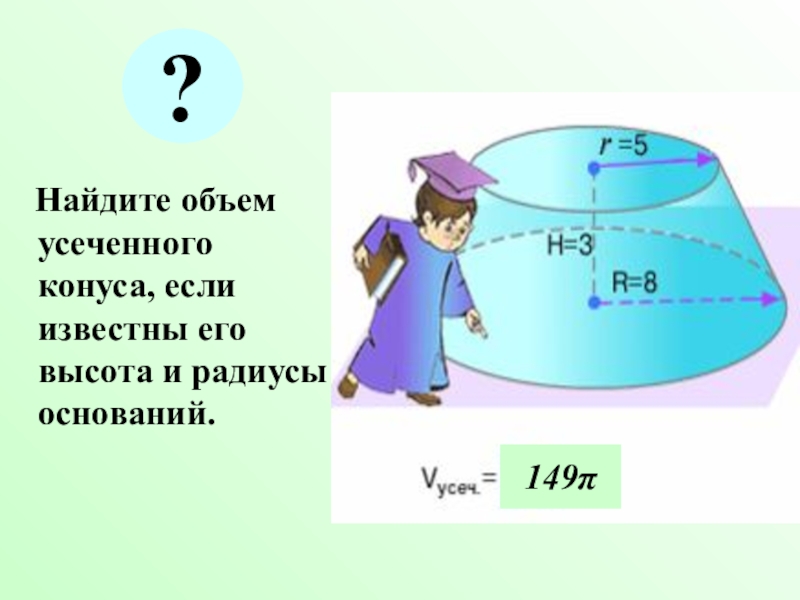
- 20. Найдите объем усеченного конуса, если известны его высота и радиусы оснований.149π?
- 21. Площади боковых поверхностей подобных цилиндров
- 22. В конусе, высота которого известна,
- 23. Домашнее заданиеГл.3 п.3 формулызадача 8, 9 с 130
- 24. Скачать презентанцию
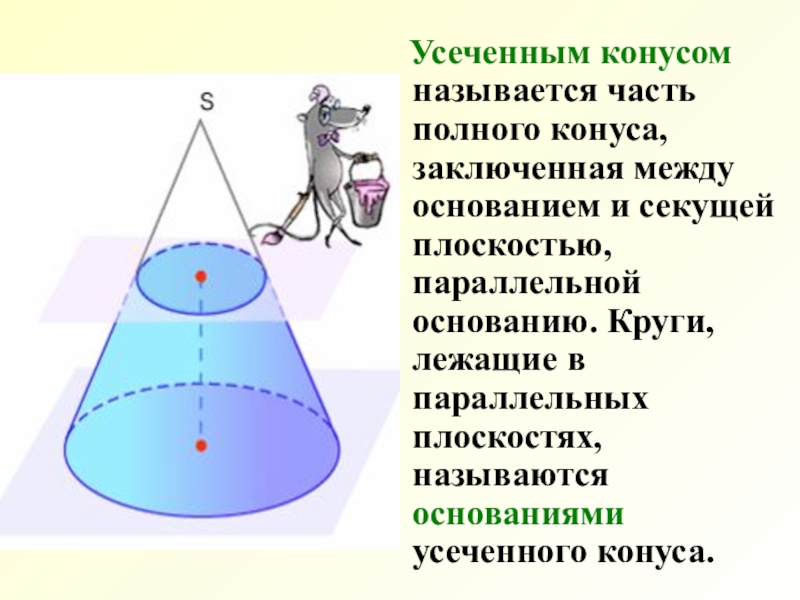
Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.
Слайды и текст этой презентации
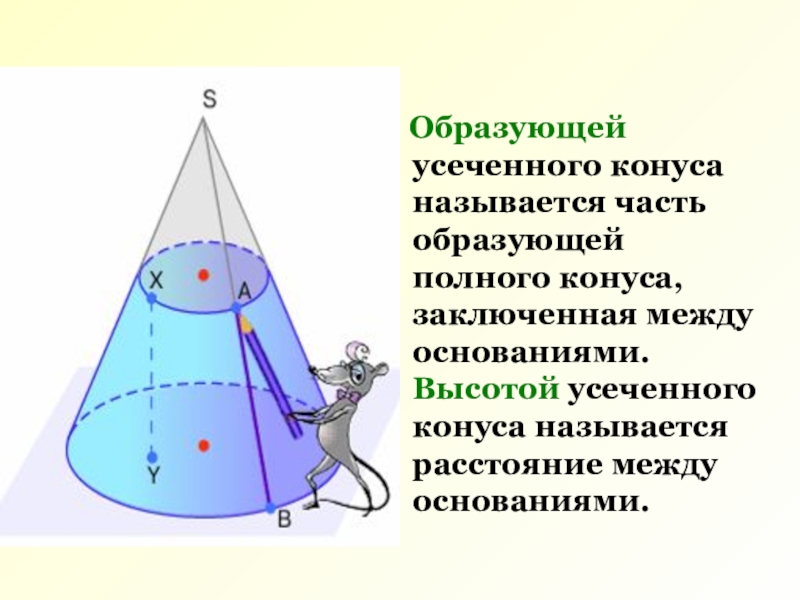
Слайд 3 Образующей усеченного конуса называется часть образующей полного конуса,
заключенная между основаниями. Высотой усеченного конуса называется расстояние между основаниями.
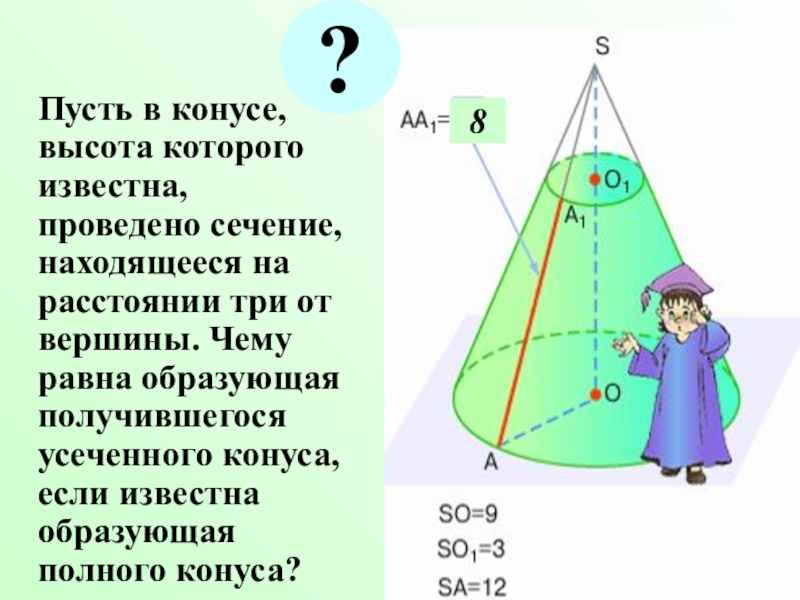
Слайд 4 Пусть в конусе, высота которого известна, проведено сечение,
находящееся на расстоянии три от вершины. Чему равна образующая получившегося
усеченного конуса, если известна образующая полного конуса?8
?
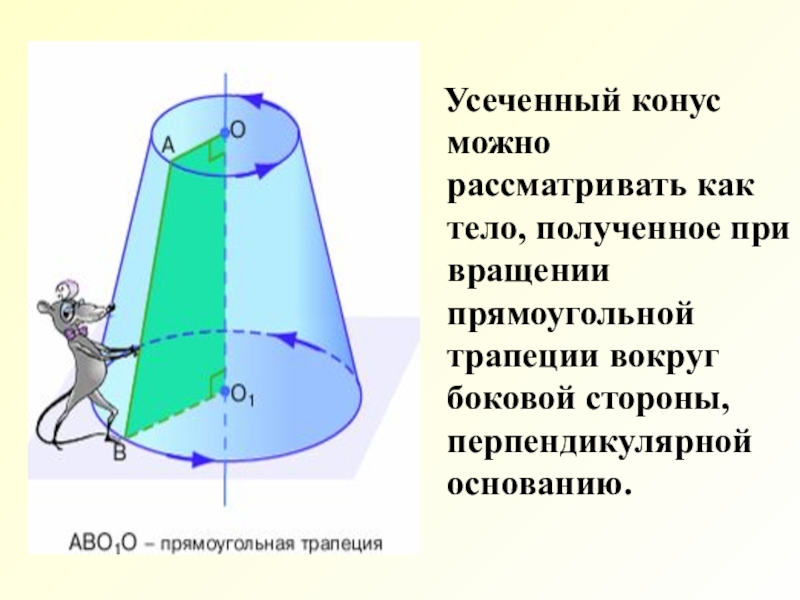
Слайд 5 Усеченный конус можно рассматривать как тело, полученное при
вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.
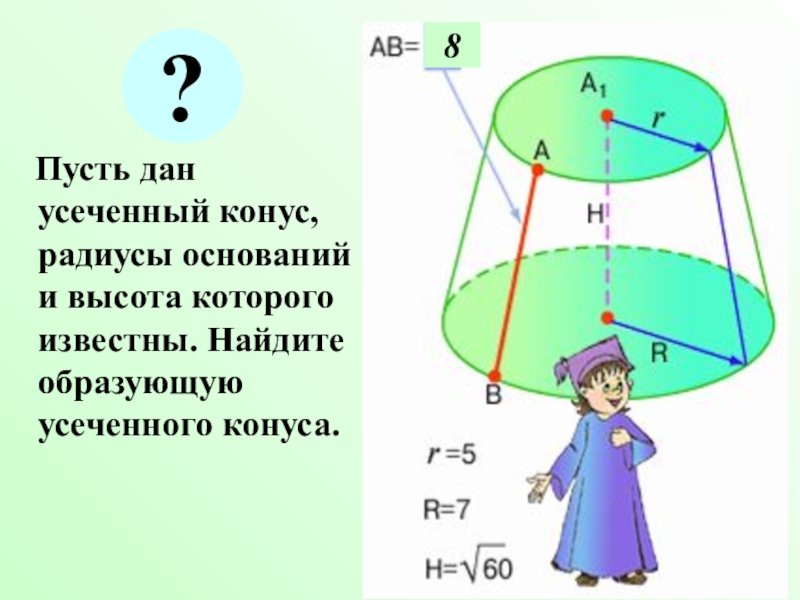
Слайд 6 Пусть дан усеченный конус, радиусы оснований и высота
которого известны. Найдите образующую усеченного конуса.
8
?
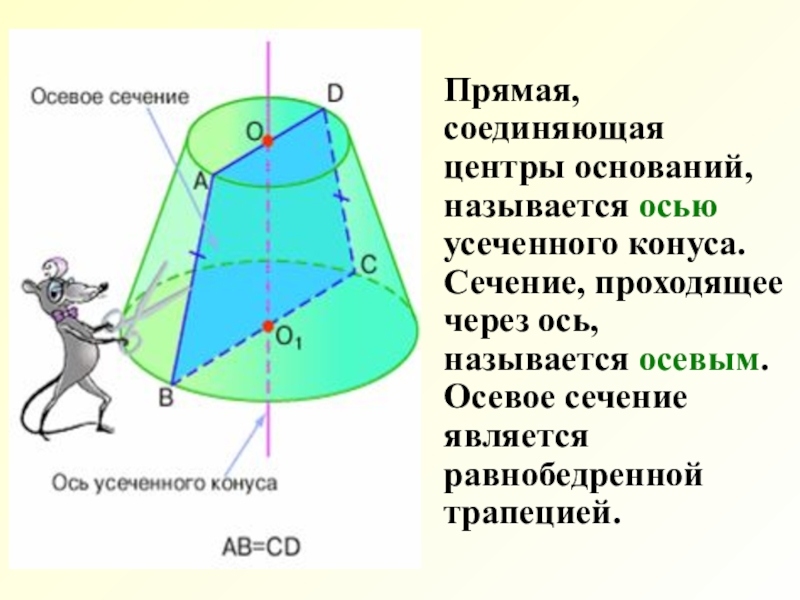
Слайд 7 Прямая, соединяющая центры оснований, называется осью усеченного конуса.
Сечение, проходящее через ось, называется осевым. Осевое сечение является равнобедренной
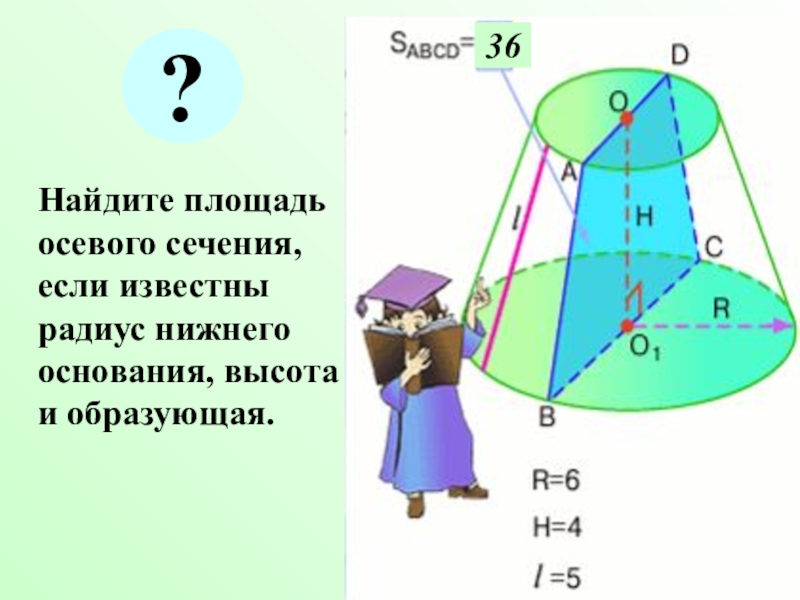
трапецией.Слайд 8 Найдите площадь осевого сечения, если известны радиус нижнего
основания, высота и образующая.
36
?
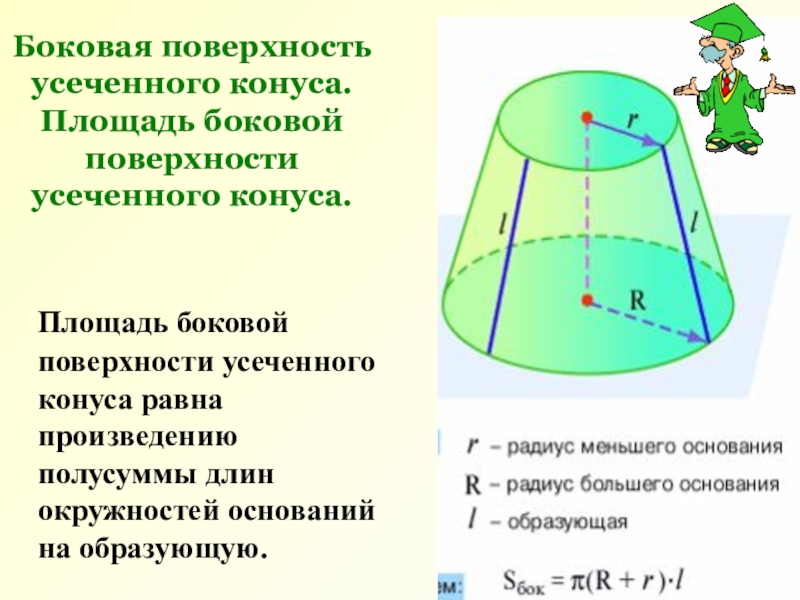
Слайд 9Боковая поверхность усеченного конуса. Площадь боковой поверхности
усеченного конуса.
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей
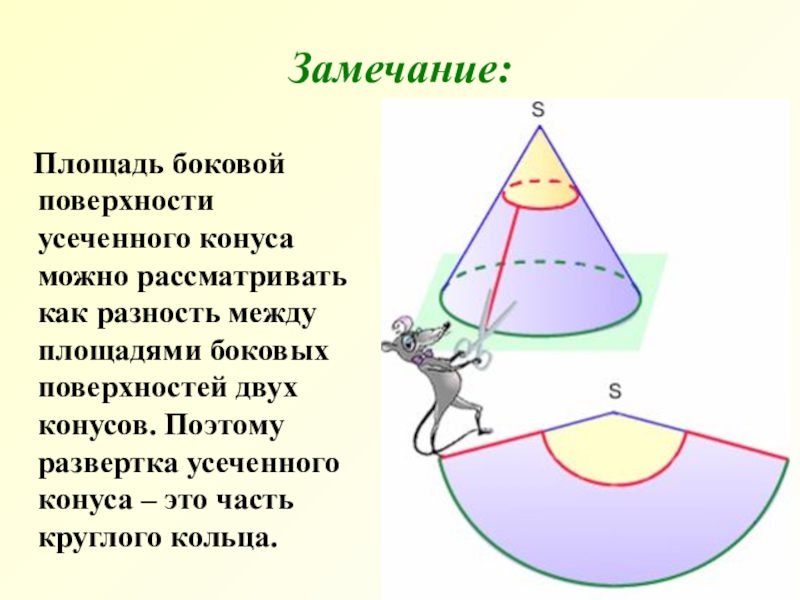
оснований на образующую.Слайд 10 Площадь боковой поверхности усеченного конуса можно рассматривать как
разность между площадями боковых поверхностей двух конусов. Поэтому развертка усеченного
конуса – это часть круглого кольца.Замечание:
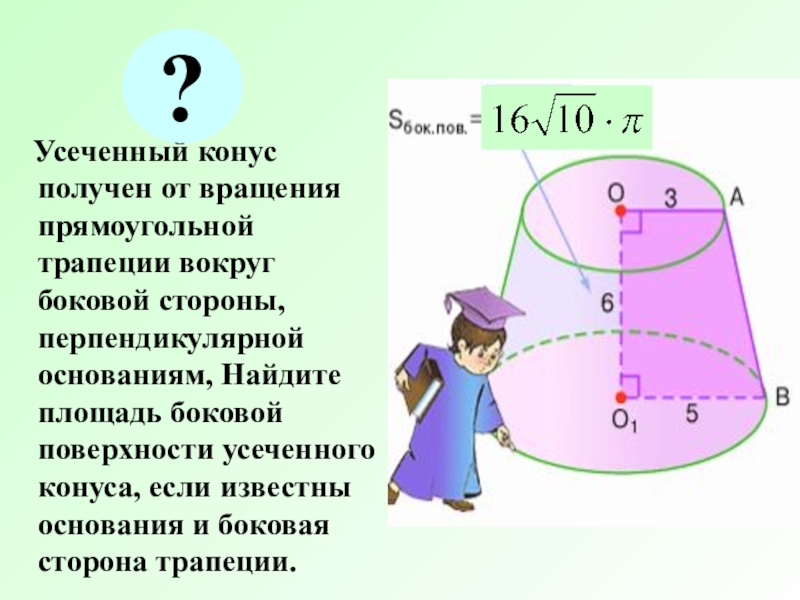
Слайд 11 Усеченный конус получен от вращения прямоугольной трапеции вокруг
боковой стороны, перпендикулярной основаниям, Найдите площадь боковой поверхности усеченного конуса,
если известны основания и боковая сторона трапеции.?
Слайд 12Задача.
Радиус меньшего основания усеченного конуса равен 5, высота равна 6,
а расстояние от центра меньшего основания до окружности большего основания
равно 10. Найдите площадь боковых поверхностей усеченного и полного конусов.Слайд 17 4) Подставим найденные значения в формулы для площадей
боковой поверхности полного и усеченного конусов.
Решение:
Слайд 18Формула объема усеченного конуса.
Объем усеченного конуса равен сумме объемов трех
конусов, имеющих одинаковую высоту с усеченным конусом, а основаниями: один
– нижнее основание этого конуса, другой – верхнее, а третий – круг, радиус которого есть среднее геометрическое между радиусами верхнего и нижнего оснований.Слайд 19 Поместим на верхнем основании усеченного конуса малый конус,
дополняющий его до полного и рассмотрим объем его как разность
объемов двух конусов.Доказательство:
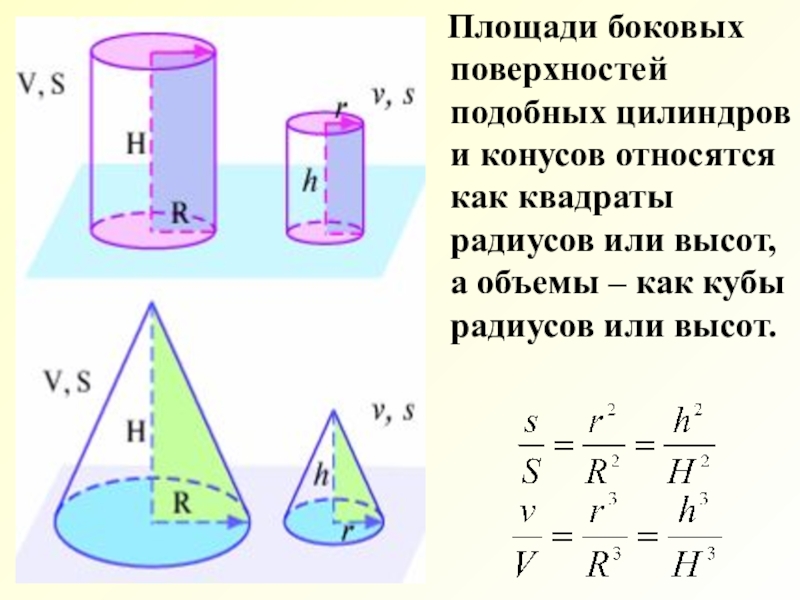
Слайд 21 Площади боковых поверхностей подобных цилиндров и конусов относятся
как квадраты радиусов или высот, а объемы – как кубы
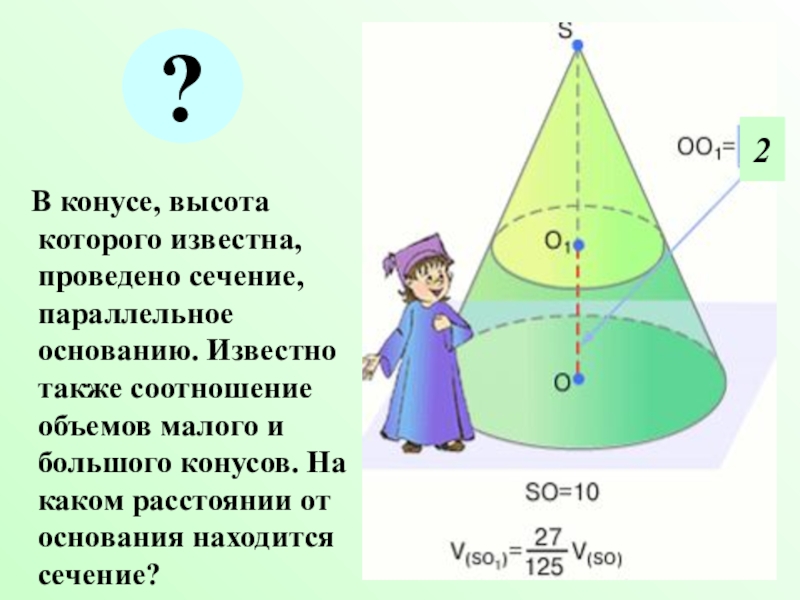
радиусов или высот.Слайд 22 В конусе, высота которого известна, проведено сечение, параллельное
основанию. Известно также соотношение объемов малого и большого конусов. На
каком расстоянии от основания находится сечение??
2