Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Условный экстремум, условия его существования и методы отыскания
Содержание
- 1. Условный экстремум, условия его существования и методы отыскания
- 2. Понятие условного экстремума функции нескольких переменных. До сих
- 3. Для решения поставленной задачи выразим у
- 4. Общая постановка задачи отыскания условного экстремума функции
- 5. Для того, чтобы точка (x0, y0) являлась
- 6. Вычислим второй дифференциал функции Лагранжа по переменным
- 7. ПРИМЕР. Найти условные экстремумы функцииz = 5 –
- 8. Вычислим второй дифференциал функции Лагранжа: Продифференцируем уравнение связи: В
- 9. Задача на условный экстремум для функции трех
- 10. Нахождение наибольшего и наименьшего значений функции на
- 11. ПРИМЕР 1.Найти наибольшее и наименьшее значения функцииz
- 12. Найдем стационарные точки функции. zx = 2x +
- 13. x = 0. Исследуем на наибольшее и наименьшее
- 14. Сравним значения функции в «подозрительных» точках: М1(–1,
- 15. ПРИМЕР 2. Найти наибольшее и наименьшее значения функцииz
- 16. Найдем стационарные точки функции. zx = 2x; zy
- 17. Вычислим значение исследуемой функции в найденных точках:Сравним
- 18. Спасибо за внимание!misis.ru
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Понятие условного экстремума функции нескольких переменных.
До сих пор мы занимались
отысканием локальных экстремумов функции, аргументы которой не связаны никакими дополнительными
условиями. Вместе с тем, в приложениях часто встречается задача об отыскании экстремума функции, аргументы которой удовлетворяют дополнительным уравнениям связи. Экстремумы такого рода называют условными.ПРИМЕР.
Пусть требуется найти экстремум функции
z = x2 + y2
при условии, что аргументы этой функции удовлетворяют уравнению связи
х + у – 1 = 0.
Таким образом, экстремумы ищутся не на всей плоскости, а а лишь на прямой х + у – 1 = 0.
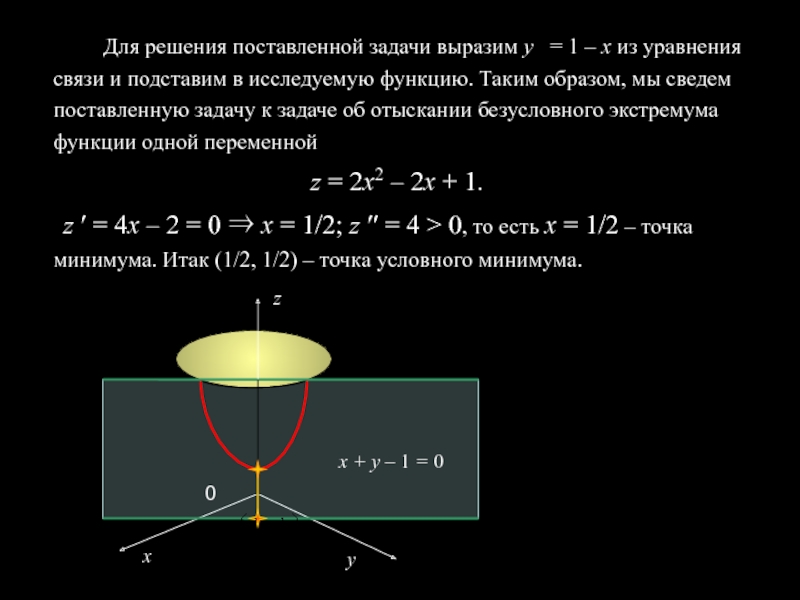
Слайд 3 Для решения поставленной задачи выразим у = 1 –
х из уравнения связи и подставим в исследуемую функцию. Таким
образом, мы сведем поставленную задачу к задаче об отыскании безусловного экстремума функции одной переменнойz = 2x2 – 2x + 1.
z ′ = 4x – 2 = 0 ⇒ x = 1/2; z ′′ = 4 > 0, то есть x = 1/2 – точка минимума. Итак (1/2, 1/2) – точка условного минимума.
Слайд 4Общая постановка задачи отыскания условного экстремума функции двух переменных.
Найти экстремумы
функции
z = f ( x, y )
(1)при условии, что ее аргументы удовлетворяют уравнению связи
ϕ ( х, у ) = 0. (2)
Эта задача может быть решена так, как в предыдущем примере. Это, так называемый, прямой метод отыскания точек условного экстремума. Однако часто уравнение связи трудно решается относительно х. Поэтому часто используют так называемый
метод множителей Лагранжа.
Пусть функции f(x, y) и ϕ (х, у) непрерывно дифференцируемы в окрестности точки (x0, y0). Составим функцию
F(x, y, λ) = f (x, y) + λϕ (х, у), (3)
которую называют функцией Лагранжа, а параметр λ – множителем Лагранжа.
Слайд 5 Для того, чтобы точка (x0, y0) являлась точкой условного экстремума
функции f(x, y) при уравнении связи ϕ (х, у) =
0, необходимо, чтобы ее координаты при некотором значении параметра λ удовлетворяли системе уравнений:Заметим, что при условии связи (2) экстремумы функции Лагранжа совпадают с экстремумами исследуемой функции (1).
Достаточные условия существования условного экстремума.
Пусть f (x, y) и ϕ (х, у) дважды непрерывно дифференцируемы в окрестности точки (x0, y0) и в этой точке выполнены необходимые условия существования условного экстремума функции f(x, y) при ограничениях (2).
Слайд 6 Вычислим второй дифференциал функции Лагранжа по переменным х и у
при фиксированном значении параметра λ, то есть
Если при выполнении условия
второй
дифференциал функции Лагранжа положительно определенная квадратичная форма, то (x0, y0) – точка условного минимума;
отрицательно определенная квадратичная форма, то (x0, y0) – точка условного максимума;
неопределенная квадратичная форма, то (x0, y0) не является точкой условного экстремума функции.
Слайд 7ПРИМЕР.
Найти условные экстремумы функции
z = 5 – 3x – 4y
относительно
уравнения связи
x2 + y2 = 25.
Составим функцию Лагранжа
F(x, y, λ)
= 5 – 3x – 4y + λ( x2 + y2 – 25).Найдем стационарные точки функции Лагранжа
Таким образом, функция f (x, y) может иметь условный экстремум только в точках (3, 4) и (–3, –4).
Слайд 8 Вычислим второй дифференциал функции Лагранжа:
Продифференцируем уравнение связи:
В точках (3, 4)
и (–3, –4) дифференциалы dx и dy связаны условием
При выполнении
этого условияСледовательно, функция f(x, y) имеет
в точке (3, 4) условный минимум z(3, 4) = – 20,
а в точке (–3, –4) – условный максимум z(–3, –4) = 30.
Слайд 9Задача на условный экстремум для функции трех переменных.
Найти экстремумы функции
u = f ( x, y, z)
при выполнении условий связи
ϕ 1 (х, у, z) = 0, ϕ 2 (х, у, z) = 0.
Здесь также возможен как прямой метод поиска условного экстремума, так и метод множителей Лагранжа.
Функция Лагранжа в данном случае имеет вид:
F(x, y, z, λ1, λ2) = f(x, y, z) + λ1ϕ 1 (х, у, z) + λ2ϕ 2 (х, у, z).
Стационарные точки этой функции находятся как решения системы
Далее исследование проводится по той же схеме, что и для функции двух переменных.
В данном случае возможно и только одно уравнение связи.
Слайд 10Нахождение наибольшего и наименьшего значений функции на компакте.
Пусть функция
u =
f(x1, x2, ... , xm) : Rm → R
непрерывна на
ограниченном замкнутом множестве G ⊂ Rm (на компакте) и дифференцируема во всех внутренних точках этого множества. Напомним, что для функции, непрерывной на компакте, существуют на этом компакте точки, в которых функция принимает наибольшее и наименьшее значения. Эти точки могут быть внутренними и граничными. Поэтому следует действовать по такой схеме:
найти стационарные точки внутри области G и вычислить значения функции в этих точках;
исследовать функцию на границе области (здесь решается задача на условный экстремум);
сравнить значения функции в стационарных точках и на границе, выбрать среди них наибольшее и наименьшее.
Слайд 11ПРИМЕР 1.
Найти наибольшее и наименьшее значения функции
z = x2 +
2xy + x + 2y
в замкнутой ограниченной области
G: y
– x ≤ 2, x ≤ 0, y ≥ 0.x
y
0
1
2
– 1
– 2
y = x + 2
y = 0
x = 0
G
Слайд 12Найдем стационарные точки функции.
zx = 2x + 2y + 1;
zy = 2x + 2.
Точка М1(–1, 1/2)∈G, z(–1,1/2) = 0.
Исследуем
функцию на границе области.y = 0.
Задача сводится к нахождению наибольшего и наименьшего значений на отрезке [– 2, 0] функции одной переменной
f ( x ) = z ( x, 0) = x2 + x.
Сначала найдем ее стационарные точки.
f ´ (x ) = 2x + 1 = 0 ⇒ x = – 1/2 ∈ [– 2, 0]. f (– 1/2) = – 1/4.
На концах отрезка f (– 2) = 2, f (0) = 0.
Следовательно, z(–1/2, 0) = – 1/4, z(–2, 0) = 2; z(0, 0) = 0.
Слайд 13x = 0.
Исследуем на наибольшее и наименьшее значение на отрезке
[0, 2] функцию
g ( y ) = z (0, y)
= 2y.Эта функция не имеет стационарных точек.
На конце отрезка g (2) = 4. Следовательно, z (0, 2) = 4.
y = x + 2.
Исследуем на наибольшее и наименьшее значение на [– 2, 0] функцию
ϕ ( x) = z ( x, x + 2) = x2 + 2x(x + 2) + x + 2(x + 2) = 3 x2 + 7 x + 4.
ϕ ´ ( x) = 6x + 7 = 0 ⇒ x = – 7/6 ∈ [– 2, 0], ϕ (– 7/6) = – 1/12.
Следовательно, z(–7/6, 5/6) = – 1/12.
Слайд 14Сравним значения функции в «подозрительных» точках:
М1(–1, 1/2), f(М1)=
0;
М2 (–2, 0), f(М2)= 2;
М3 (0, 0), f(М3)=
0;М4 (0, 2), f(М4)= 4;
М5 (–1/2, 0), f(М5)= –1/4;
М6 (–7/6, 5/6), f(М6)= –1/12.
В результате получим, что
zнаиб = 4 в точке М4 (0, 2) ,
zнаим = –1/4 в точке М5 (–1/2, 0) .
x
y
0
– 2
2
M1
M2
M3
M4
M6
M5
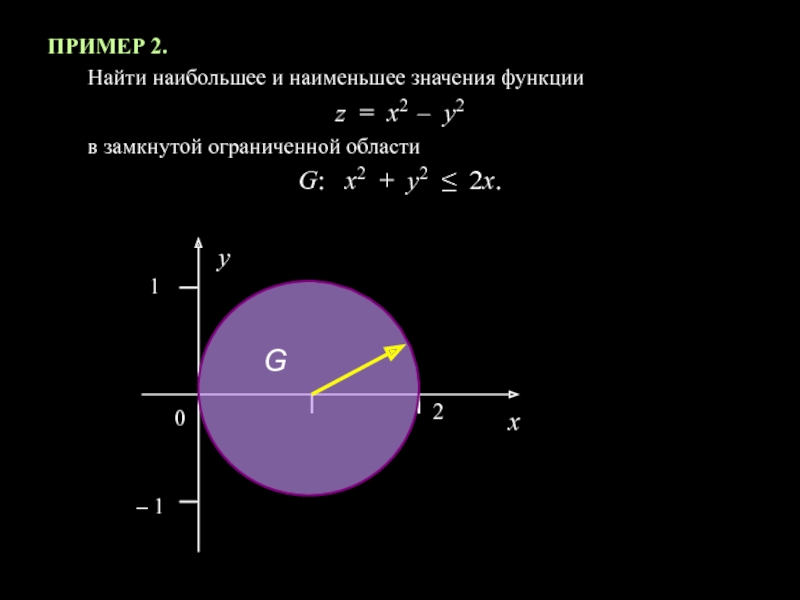
Слайд 15ПРИМЕР 2.
Найти наибольшее и наименьшее значения функции
z = x2 –
y2
в замкнутой ограниченной области
G: x2 + y2 ≤ 2x.
x
y
0
–
11
2
G
Слайд 16Найдем стационарные точки функции.
zx = 2x; zy = – 2y.
М1(0, 0) – стационарная точка. z(0, 0) = 0.
Исследуем функцию
на границе области.Будем решать задачу на условный экстремум, то есть найдем наибольшее и наименьшее значения функции
z = x2 – y2,
аргументы которой удовлетворяют уравнению связи
x2 + y2 – 2x = 0.
Составим функцию Лагранжа
F(x, y, λ) = x2 – y2 + λ( x2 + y2 – 2x).
Найдем стационарные точки функции Лагранжа
Слайд 17
Вычислим значение исследуемой функции в найденных точках:
Сравним значения функции в
точках
М1(0, 0), М2(2, 0),
В результате получим:
zнаиб = 4 в
точке М2(2, 0), zнаим = в











![Условный экстремум, условия его существования и методы отыскания x = 0. Исследуем на наибольшее и наименьшее значение на отрезке [0, x = 0. Исследуем на наибольшее и наименьшее значение на отрезке [0, 2] функциюg ( y ) =](/img/thumbs/86ee5f7a9b38ccabaa48ef802bc10add-800x.jpg)