Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УСТОЙЧИВОСТЬ ЭНЕРГОСИСТЕМ
Содержание
- 1. УСТОЙЧИВОСТЬ ЭНЕРГОСИСТЕМ
- 2. Физические основы устойчивости электроэнергетических систем Статическая устойчивость
- 3. Физические основы устойчивости электроэнергетических системВ установившемся режиме
- 4. Физические основы устойчивости электроэнергетических системИз определения устойчивости
- 5. Физические основы устойчивости электроэнергетических системПри этом условии
- 6. Физические основы устойчивости электроэнергетических системДля обеспечения устойчивости
- 7. Физические основы устойчивости электроэнергетических системЧтобы проверить статическую
- 8. Статическая устойчивость системы «эквивалентный генератор - шины
- 9. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
- 10. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ Анализируемая электростанция связана через трансформаторные
- 11. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬНа рис.11.1, б представлены два основных
- 12. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬДля получения характеристики мощности генератора построена
- 13. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬИз векторной диаграммы следует, что
- 14. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬЗависимость (11.1) имеет синусоидальный характер и
- 15. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬПри определённых значениях ЭДС генератора и
- 16. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
- 17. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬРассмотрим режим работы в точке а.
- 18. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬНеобходимо подчеркнуть, что перемещение ротора под
- 19. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬЕсли уменьшить мощность генератора в точке
- 20. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬЕсли в точке b мощность генератора
- 21. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬТаким образом, признаком статической устойчивости электрической
- 22. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬОчевидно, что в условиях эксплуатации генератор
- 23. СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬРуководящими указаниями по устойчивости энергосистем предписано,
- 24. Характеристика мощности явнополюсного генератора Для характеристики мощности
- 25. Характеристика мощности явнополюсного генератораИз последнего выражения следует,
- 26. Характеристика мощности явнополюсного генератораХарактеристика явнополюсной машины
- 27. Характеристика мощности явнополюсного генератораАмплитуда характеристики мощности возрастает
- 28. Характеристика мощности генератора с АРВ Предположим, что
- 29. Характеристика мощности генератора с АРВ
- 30. Характеристика мощности генератора с АРВВектор напряжения на
- 31. Характеристика мощности генератора с АРВУмножая левую и
- 32. Характеристика мощности генератора с АРВИз диаграммы следует,
- 33. Характеристика мощности генератора с АРВ
- 34. Характеристика мощности генератора с АРВЕсли принять за
- 35. Характеристика мощности генератора с АРВРегуляторы пропорционального типа
- 36. Характеристика мощности генератора с АРВЭто связано с
- 37. Характеристика мощности генератора с АРВХарактеристика мощности при
- 38. Характеристика мощности генератора с АРВ
- 39. Характеристика мощности генератора с АРВХарактеристика мощности генератора,
- 40. Характеристика мощности генератора с АРВЕсли РПТ имеет
- 41. Характеристика мощности генератора с АРВРегулятор начинает работать
- 42. Характеристика мощности генератора с АРВ
- 43. Характеристика мощности генератора с АРВПусть исходному режиму
- 44. Характеристика мощности генератора с АРВУвеличение тока возбуждения,
- 45. Характеристика мощности генератора с АРВПосле того как
- 46. Характеристика мощности генератора с АРВОбеспечить устойчивую работу
- 47. Скачать презентанцию
Физические основы устойчивости электроэнергетических систем Статическая устойчивость энергосистемы – это устойчивость при малых возмущениях режима. Из рассмотрения простейших механических систем следует, что есть состояния (режимы), в которых система после случайного возмущения
Слайды и текст этой презентации
Слайд 2Физические основы устойчивости электроэнергетических систем
Статическая устойчивость энергосистемы – это
Слайд 3Физические основы устойчивости электроэнергетических систем
В установившемся режиме между энергией
источника
, поступающей в систему, и энергией, расходуемой в нагрузке и
на покрытие потерь, имеется баланс. При каком–либо возмущении, проявляющемся в изменении параметра режимана , этот баланс нарушается.
Если система обладает такими свойствами, что энергия
после возмущения расходуется более интенсивно, чем вырабатывается электростанциями , то новый режим, возникший в результате возмущения, не может быть обеспечен энергией и в системе должен восстановиться прежний установившийся или близкий к нему режим. Такая система устойчива.
Слайд 4Физические основы устойчивости электроэнергетических систем
Из определения устойчивости следует, что условием
сохранения устойчивости системы (критерием устойчивости) является соотношение
,или в дифференциальной форме
.
Величину называют избыточной энергией. Эта энергия положительна, если дополнительная генерируемая энергия, появившаяся при возмущении, возрастет интенсивнее, чем нагрузка системы с учётом потерь в ней.
Слайд 5Физические основы устойчивости электроэнергетических систем
При этом условии критерий устойчивости запишется
в виде
,т.е. режим устойчив, если производная от избыточной энергии по определяющему параметру отрицательна.
Слайд 6Физические основы устойчивости электроэнергетических систем
Для обеспечения устойчивости системы существенное значение
имеет запас её статической устойчивости, который характеризуется углами сдвига роторов
генераторов и векторов напряжений в узловых точках системы. Большое значение имеет запас статической устойчивости в послеаварийном режиме – по мощности электрической передачи он должен составлять5 – 10 %, в нормальном же режиме 15 – 20 %. Однако эти цифры строго не лимитируются.
Слайд 7Физические основы устойчивости электроэнергетических систем
Чтобы проверить статическую устойчивость системы, необходимо
составить дифференциальные уравнения малых колебаний для всех его элементов и
регулирующих устройств, а затем исследовать корни характеристического уравнения на устойчивость. Поскольку строгое решение такой задачи очень сложно, в инженерных расчётах применяются приближённые методы исследования устойчивости, которые основываются на использовании практических критериев устойчивости.Слайд 8Статическая устойчивость системы «эквивалентный генератор - шины постоянного напряжения»
Система в
которой одиночная удалённая электростанция связана с шинами (системой) постоянного по
величине напряжения, называется простейшей (рис.11.1, а). Считается, что суммарная мощность электрических станций системы значительно превышает мощность рассматриваемой станции. Это позволяет считать напряжение на шинах системы неизменным при любых режимах её работы. Простейшей система называется ещё одномашинной моделью энергосистемы или модель «машина – шины».Слайд 10СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Анализируемая электростанция связана через трансформаторные связи и линию электропередачи
с генераторами мощной концентрированной энергосистемы, настолько мощной, что её приёмные
шины обозначают как шины бесконечной мощности (ШБМ). Отличительными признаками ШБМ являются неизменное по модулю напряжение и неизменная частота этого напряжения. При использовании ШБМ, соответствующие им энергосистемы в электрических схемах, как правило, не изображаются. В схемах замещения шины бесконечной мощности используются как элемент, изображающий мощную систему.Слайд 11СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
На рис.11.1, б представлены два основных агрегата тепловой электрической
станции: турбина и генератор. Вращающий момент турбины зависит от количества
подводимого энергоносителя: для паровой турбины – это пар, для гидротурбины – вода. В нормальном режиме основные параметры энергоносителя стабильны, поэтому вращающий момент постоянный. Мощность, выдаваемая генератором в систему, определяется несколькими параметрами, влияние которых зависит от характеристики мощности генератора.Слайд 12СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Для получения характеристики мощности генератора построена векторная диаграмма электропередачи
(рис. 11.1, в). Здесь полный вектор тока разложен на его
действительную и мнимую составляющие, а сопротивление получено из схемы замещения системы, представленной на рис. 11.1, г:Слайд 13СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Из векторной диаграммы следует, что
,
где – активная составляющая тока, – угол сдвига вектора ЭДС относительно вектора напряжения . Умножая обе части равенства на , получим,
(11.1)
где – активная мощность, выдаваемая генератором (принята в относительных единицах).
Слайд 14СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Зависимость (11.1) имеет синусоидальный характер и называется характеристикой мощности
генератора. При постоянных ЭДС генератора и напряжения угол поворота ротора
генератора определяется только его активной мощностью, которая в свою очередь определяется мощностью турбины.Мощность турбины зависит от количества энергоносителя, и в координатах , изображается прямой линией.
Слайд 15СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
При определённых значениях ЭДС генератора и напряжения приёмной стороны
характеристика мощности имеет максимум, который вычисляется по формуле
. (11.2)Величину называют также «идеальным» пределом мощности электрической системы. Каждому значению мощности турбины соответствуют две точки пересечения характеристики а и b (рис.11.2, а), в которых мощности генератора и турбины равны между собой.
Слайд 17СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Рассмотрим режим работы в точке а. Если мощность генератора
увеличить на величину , то и угол , следуя синусоидальной
зависимости, изменится на величину . Из рис. 11.2, а следует, что в точке а положительному приращению мощности, соответствует положительное приращение угла.При изменении мощности генератора равновесие моментов турбины и генератора нарушается. При увеличении мощности генератора на валу ротора, связывающего его с турбиной возникает тормозящий момент, превышающий вращающий момент турбины. Тормозящий момент вызывает замедление ротора генератора, что вызывает перемещение ротора и связанного с ним вектора ЭДС в сторону уменьшения угла (рис.11.2, б).
Слайд 18СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Необходимо подчеркнуть, что перемещение ротора под действием избыточного момента
накладывается на его движение в положительном направлении с синхронной скоростью,
которая во много раз превышает скорость этого перемещения. В итоге в точке а восстанавливается исходный режим работы и, как следует из определения статической устойчивости, этот режим является устойчивым. Такой же вывод можно получить и при уменьшении мощности генератора в точке а.Слайд 19СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Если уменьшить мощность генератора в точке b, то на
валу ротора генератора возникает ускоряющий избыточный момент, который увеличивает угол
. С ростом угла мощность генератора ещё уменьшается, это приводит к дополнительному увеличению ускоряющего момента, таким образом, возникает лавинообразный процесс, который называют выпадением из синхронизма. Процесс выпадения из синхронизма и асинхронный режим, в котором в итоге оказывается генератор, характеризуется непрерывным перемещением вектора ЭДС относительно напряжения приёмной системы.Слайд 20СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Если в точке b мощность генератора увеличить, то возникнет
избыточный тормозной момент, который вызовет перемещение рабочей точки системы турбина–генератор
в точку а.Таким образом, точка а характеристики мощности является точкой устойчивого равновесия моментов турбины и генератора, точка b – точкой неустойчивого равновесия. Аналогично все точки, лежащие на возрастающей части характеристики мощности, являются точками устойчивой работы системы, а точки, лежащие на падающей части характеристики, – точками неустойчивой работы. Границей зон устойчивой и неустойчивой работы является максимум характеристики мощности.
Слайд 21СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Таким образом, признаком статической устойчивости электрической системы является знак
приращения мощности к приращению угла. Если , то
система устойчива,
если это отношение отрицательно, то неустойчива. Переходя к пределу, получим критерий устойчивости простейшей системы:.
Увеличение мощности турбины от значения до (рис.11.2, а) приводит к возрастанию угла ротора от значения до значения и к снижению статической устойчивости.
Слайд 22СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Очевидно, что в условиях эксплуатации генератор не следует загружать
до предельной мощности , так как любое незначительное отклонение
параметров режима может привести к потере синхронизма и переходу генератора в асинхронный режим. На случай появления непредвиденных возмущений предусматривается запас по загрузке генератора, характеризуемый коэффициентом запаса статической устойчивости. (11.3)
Слайд 23СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
Руководящими указаниями по устойчивости энергосистем предписано, что в нормальных
режимах энергосистем должен обеспечиваться запас устойчивости электропередачи, связывающей станцию с
шинами энергосистемы не менее 20% в нормальном режиме и 8% в кратковременном послеаварийном. В наиболее тяжёлых режимах, при которых увеличение перетоков мощности по линиям позволяет уменьшить ограничения потребителей или потери гидроресурсов, допускается снижение запаса по устойчивости до 8%.Под кратковременными понимаются послеаварийные режимы длительностью до 40 минут, в течение которых диспетчер должен восстановить нормальный запас по статической устойчивости.
Слайд 24Характеристика мощности явнополюсного генератора
Для характеристики мощности явнополюсной машины запишем
выражение активной мощности, выдаваемой в систему
Учитывая, что
, выражение для мощности перепишем в виде Слайд 25Характеристика мощности явнополюсного генератора
Из последнего выражения следует, что характеристика мощности
явнополюсного генератора кроме основной синусоидальной составляющей содержит вторую составляющую –
вторую гармоническую составляющую, амплитуда которой пропорциональна разности индуктивных сопротивлений и . Вторая гармоника смещает максимум характеристики мощности в сторону уменьшения угла (рис. 11.3).Первая, основная часть зависит от величины ЭДС, что говорит о том, что генератор должен быть возбуждён. Вторая составляющая не зависит от возбуждения генератора, она показывает, что явнополюсный генератор может выдавать активную мощность без его возбуждения за счёт реактивного момента, но эта активная мощность зависит от синуса двойного угла.
Слайд 27Характеристика мощности явнополюсного генератора
Амплитуда характеристики мощности возрастает по сравнению с
характеристикой неявнополюсной машины. Но это увеличение проявляется только при малых
значениях ЭДС (когда первая и вторая составляющие имеют одинаковый порядок).В обычных условиях амплитуда второй гармоники составляет 10 – 15% основной гармоники и не оказывает заметного влияния на характеристику мощности.
Слайд 28Характеристика мощности генератора с АРВ
Предположим, что у генератора на
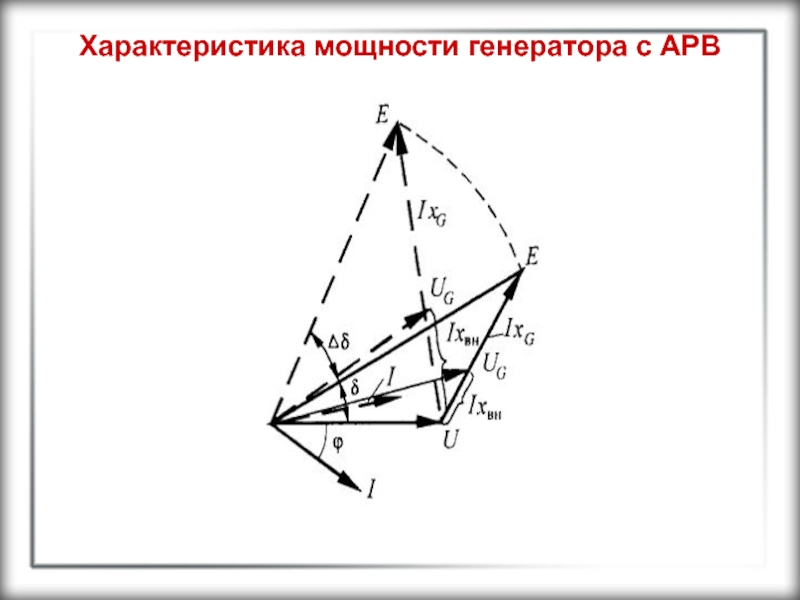
рис. 11.1 отключена система регулирования напряжения. Построим векторную диаграмму рассматриваемой
системы, выделив в ней напряжение на шинах генератора (рис.11.4, а). Оно зависит от падения напряжения на внешнем сопротивлении системы:где – внешнее сопротивление системы.
Слайд 30Характеристика мощности генератора с АРВ
Вектор напряжения на шинах генератора делит
вектор падения напряжения на две части, пропорциональные индуктивным сопротивлениям
и . Увеличим передаваемую активную мощность на и тем самым угол на . Это вызовет изменение реактивной мощности, передаваемой в систему. Для получения зависимости реактивной мощности от угла запишем выражение, следующее из векторной диаграммы, показанной на рис. 11.1, вСлайд 31Характеристика мощности генератора с АРВ
Умножая левую и правую части последнего
равенства на , получим
.
Выразив , из последнего
соотношения, получим выражение для реактивной мощности, выдаваемой генератором от угла :.
Слайд 32Характеристика мощности генератора с АРВ
Из диаграммы следует, что увеличение угла
вызывает уменьшение напряжения на шинах генератора.
Предположим, что автоматический регулятор возбуждения
включён и контролирует напряжение . При понижении этого напряжения регулятор увеличивает ток возбуждения, а вместе с ним и ЭДС до тех пор пока не восстановится прежнее значение напряжения.Рассматривая установившиеся режимы работы генератора с АРВ при различных значениях угла , часто исходят из постоянства напряжения . На рис. 11.4, б показано семейство характеристик , построенных для различных значений ЭДС.
Слайд 34Характеристика мощности генератора с АРВ
Если принять за исходную точку нормального
режима точку а, то для увеличения мощности (сопровождающемся увеличением угла
) точки новых установившихся режимов будут определяться переходом с одной характеристики на другую в соответствии с векторной диаграммой (рис.11.4, а). Соединив между собой точки установившихся при различных уровнях возбуждения, получим внешнюю характеристику генератора. Она возрастает даже в области углов о , и её максимум достигается при угле о, где – угол вектора напряжения на шинах генератора . Но возможность работы в области углов больше 90о зависит от типа регулятора возбуждения.Слайд 35Характеристика мощности генератора с АРВ
Регуляторы пропорционального типа (РПТ) при коэффициентах
усиления 50…100 позволяют поддерживать напряжение на шинах генератора практически
постоянным . Коэффициент усиления определяется как отношение чисел единиц возбуждения и единиц напряжения генератора. Но предельная мощность передачи такого генератора, снабжённого АРВ с таким коэффициентом усиления, незначительно выше предельной мощности нерегулируемого генератора.Слайд 36Характеристика мощности генератора с АРВ
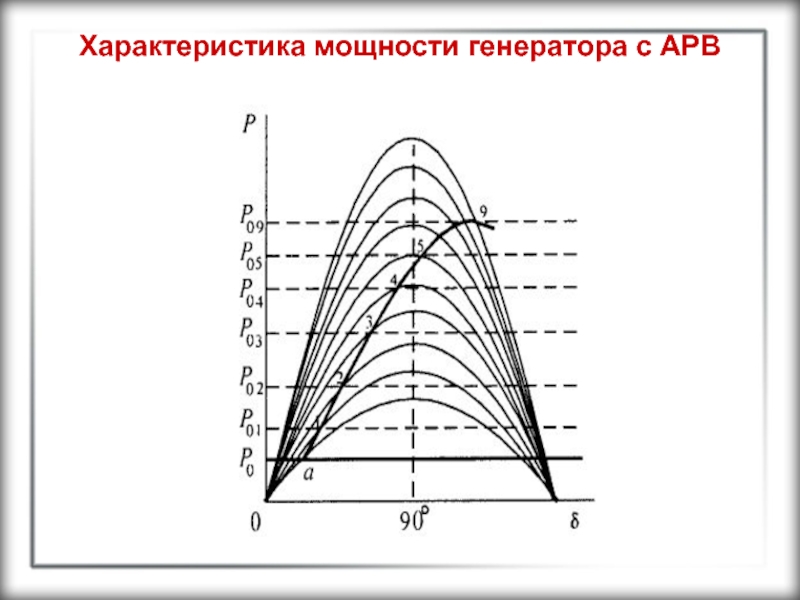
Это связано с тем, что при
увеличении мощности в некоторой точке характеристики мощности (точка 3 на
рис. 11.5, а) начинается самораскачивание генератора, т.е. периодические колебания ротора с увеличивающейся амплитудой приводят к выпадению генератора из синхронизма. Поэтому регуляторами пропорционального типа не стараются поддержать , допуская его некоторое снижение с ростом нагрузки. В этом случае предельная мощность , которой удаётся достигнуть, значительно выше мощности (рис.11.5, б).Слайд 37Характеристика мощности генератора с АРВ
Характеристика мощности при коэффициентах усиления порядка
20…40 имеет примерно такой же максимум, что и
характеристика генератора при . Следовательно, генератор, снабжённый регулятором пропорционального типа, может быть представлен в схемах замещения переходными ЭДС и сопротивлением .Слайд 39Характеристика мощности генератора с АРВ
Характеристика мощности генератора, замещаемого ЭДС
, может быть получена так же, как и характеристика явнополюсного
генератораСлайд 40Характеристика мощности генератора с АРВ
Если РПТ имеет зону нечувствительности, критическим
считается режим при
о, т.е. предельная мощность достигается в точке
в Слайд 41Характеристика мощности генератора с АРВ
Регулятор начинает работать лишь после того,
как отклонение напряжения в ту или иную сторону достигнет определённого
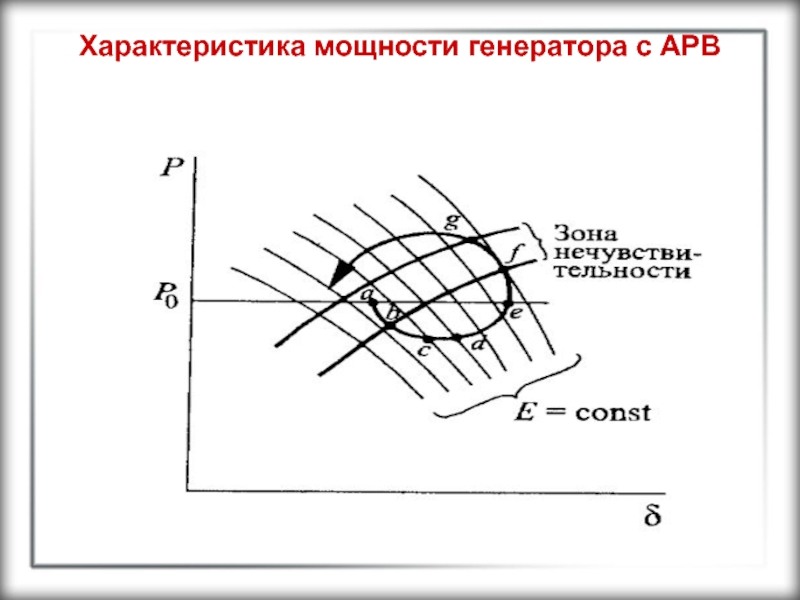
значения. При меньших отклонениях, лежащих в зоне нечувствительности, регулятор не работает. Границам зоны нечувствительности соответствуют две внешние характеристики (рис.11.6).Слайд 43Характеристика мощности генератора с АРВ
Пусть исходному режиму соответствует точка а.
При небольшом возмущении, вызывающем увеличение угла, уменьшается напряжение на шинах
генератора, но регулятор не работает до тех пор, пока отклонение угла лежит в зоне нечувствительности. При увеличении угла на валу генератора возникает ускоряющий избыточный момент, вызывающий его дальнейшее увеличение. Когда угол движения пересекает границу зоны нечувствительности (точка b), регулятор начинает работать.Слайд 44Характеристика мощности генератора с АРВ
Увеличение тока возбуждения, а, следовательно, и
ЭДС генератора, замедляет снижение мощности, перемещая рабочую точку на характеристике
мощности, соответствующие большим ЭДС (точки с, d). В точке е избыток мощности становится равным нулю, но вследствие инерции ротора продолжается увеличение угла . В точке f угол становится максимальным, после чего начинает уменьшаться.Слайд 45Характеристика мощности генератора с АРВ
После того как будет пройдена точка
g, лежащая на внешней характеристике, регулятор начнёт уменьшать напряжение возбудителя
и кривая изменения мощности пересечёт внутренние характеристики мощности в обратном направлении. Таким образом, в силу внутренней неустойчивости возникают незатухающие колебания ротора генератора (колебания угла ). Амплитуда этих колебаний зависит от ширины зоны нечувствительности регулятора. Вместе с углом колеблются напряжение, мощность и ток генератора. Такие колебания затрудняют контроль работы генератора и вызывают необходимость отказаться от его эксплуатации в подобных режимах.Слайд 46Характеристика мощности генератора с АРВ
Обеспечить устойчивую работу генератора при
о, возможно при использовании более сложных регуляторов возбуждения, которые реагируют
не только на изменение величины напряжения, но и на скорость и даже ускорение изменения величины напряжения. Такие регуляторы называются регуляторами сильного действия.Регуляторы сильного действия обеспечивают постоянное напряжение на выводах генератора (без самораскачивания), поэтому генератор, снабжённый таким регулятором, при расчёте статической устойчивости на схеме замещения может быть представлен источником постоянного напряжения с нулевым сопротивлением .