Валентинов В.А. Эконометрика. Лекция 8. Обобщенный метод наименьших квадратов

(ОМНК) (модуль 2)

8.1. Область использования ОМНК
8.2. Анализ третьей и четвертой

предпосылок МНК
8.3. Использование ОМНК при гомоскедастичных остатках
8.4. Использование ОМНК при наличии автокорреляции остатков

(ОМНК) (модуль 2)
8.1. Область использования ОМНК
Обобщенный метод

наименьших квадратов иногда называют методом взвешенных наименьших квадратов является одним из методов устранения нарушений 3 и 4 предпосылок МНК с помощью преобразования данных.
После преобразования получается новая модель, в которой не всегда удается дать экономическую интерпретацию как коэффициентам, так и переменным.
Взвешенная регрессия, основанная на ОМНК, получила широкое применение, с помощью которой можно приближать расчетные значения функции к наиболее важным значениям зависимой переменной.
Оценки параметров модели, выполненных с помощью ОМНК для автокорреляции остатков, позволяют улучшить модель.

(ОМНК) (модуль 2)
8.2. Анализ третьей и четвертой предпосылок МНК
Изучим более

подробно 3 и 4 предпосылку МНК:
3 - Остатки являются гомоскедастичными;
4 - Отсутствие автокорреляции остатков.
Представим уравнение модели в матричном виде:
У = ХА + е.
Для модели с объемом выборки, равного пяти:






где М – знак математического ожидания, ( математическое ожидание равно среднему значению, при увеличении измерений, стремящихся к бесконечности),
е - вектор столбец остатков модели:






е' – транспонированный вектор столбец остатков модели:

(ОМНК) (модуль 2)
ее' – матричное произведение: первой матрицы е на

вторую матрицу е'








Математическое выражение М(ее') можно записать более компактно в двух вариантах.
Первый вариант:
М(ее') = ϭ2Ω
ϭ2 – константа - дисперсия остатков, которая считается неизвестной,
Ω - матрица, показывающая структуру М(ее'), которая считается известной.
Второй вариант:
М(ее') = V
V – матрица, элементы которой считаются известными на основании многократных определения остатков модели на различных выборках равного объема.

(ОМНК) (модуль 2)
Если предпосылки 3 и 4 выполняются,

то Ω = I, следовательно
М(ее') = ϭ2I ,
где I - единичная матрица.





Матрица ϭ2I будет иметь следующий вид:







Единичная матрица I показывает структуру М(ее').
В единичной матрице недиагональные элементы равны нулю, следовательно, автокорреляция остатков равна нулю или отсутствует, диагональные элементы равны 1, следовательно, дисперсии остатков равны между собой или однородны или гомоскедастичны.

(ОМНК) (модуль 2)
Нарушение предпосылок 3 и (или) 4

МНК записывается следующим соотношением:
М(ее')  ϭ2I,
При нарушении предпосылок 3 и (или) 4 оценки параметров модели, вычисленные по формуле


будут несмещенными, состоятельными, но неэффективными.
Для того, чтобы оценки параметров модели, при наличии нарушений предпосылок 3 или 4, были несмещенными, состоятельными и эффективными, можно использовать формулу обобщенного метода наименьших квадратов (ОМНК) или метод Эйткена:
 

где В – вектор столбец коэффициентов модели, вычисленных по методу Эйткена;
Х – матрица значений факторов,
У – вектор столбец зависимой переменной,
V = М(ее') – матрица симметрическая, положительно определенная,
V-1 – обратная матрица от V.

(ОМНК) (модуль 2)
Расчеты коэффициентов по предложенной формуле

метода Эйткена можно выполнить, если известна матрица V, которая вычисляется на основе известных значений остатков с помощью средних значений (ее'), являющихся оценкой М(ее').
К сожалению, не от каждой матрицы V можно получить обратную матрицу.
Метод Эйткена не является универсальным и может использоваться только при определенной структуре матрицы V.
Изучение ОМНК сведется к конкретным рекомендациям по такому преобразованию факторов и зависимой переменной, после которых будет устранена гетероскедастичность и автокорреляция остатков.
При этом после преобразования переменных Х и У возникает новая модель, в которой иногда удается дать экономическую интерпретацию новых переменных и новых коэффициентов новой модели.

(ОМНК) (модуль 2)
Известны два условия, при которых можно

найти обратную матрицу от V.
Первое условие: если матрица V является диагональной, это означает наличие или отсутствие гетероскедастичности остатков, автокорреляция остатков равна нулю.
Диагональная матрица - квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю.
Второе условие: если матрица V имеет одинаковые диагональные элементы или гетероскедастичность отсутствует, не диагональные элементы расположены так, что определитель матрицы не равен нулю или имеется автокорреляция остатков.
Выполнение первого условия позволяет устранить гетероскедастичность остатков.
Выполнение второго условия позволяет устранить автокорреляцию остатков.
Однако, ученым пока не удалось одновременно устранить и гетероскедастичность и автокорреляцию остатков.

(ОМНК) (модуль 2)
8.3. Использование ОМНК при гетероскедастичных остатках

Рассмотрим более подробно первое условие - если матрица V является диагональной, это означает наличие или отсутствие гетероскедастичности остатков, автокорреляция остатков равна нулю.
Допустим, матрица V является диагональной





Четвертому значению диагонали было дано значение 10, остальным элементам диагонали были даны значения, равные 1.
Обратная матрица от V будет иметь следующий вид:

(ОМНК) (модуль 2)
Вычислим коэффициенты линейной модели У=а0+а1*Х+е двумя

методами: МНК и ОМНК, сравним их значения









Приводим значения коэффициентов линейной модели , вычисленных МНК по формуле:




Приводим значения коэффициентов линейной модели, вычисленных ОМНК по формуле: В = (Х'V-1Х)-1 Х'V-1У

(ОМНК) (модуль 2)
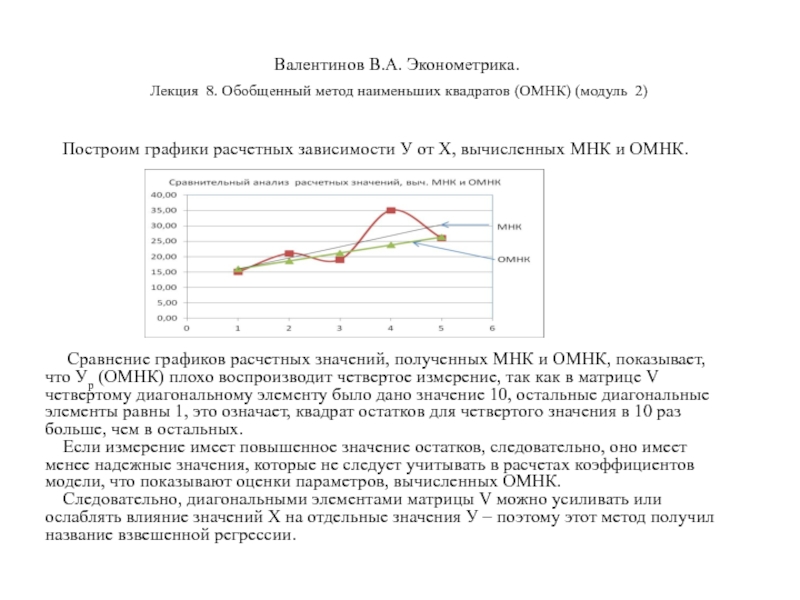
Построим графики расчетных зависимости У

от Х, вычисленных МНК и ОМНК.











Сравнение графиков расчетных значений, полученных МНК и ОМНК, показывает, что Ур (ОМНК) плохо воспроизводит четвертое измерение, так как в матрице V четвертому диагональному элементу было дано значение 10, остальные диагональные элементы равны 1, это означает, квадрат остатков для четвертого значения в 10 раз больше, чем в остальных.
Если измерение имеет повышенное значение остатков, следовательно, оно имеет менее надежные значения, которые не следует учитывать в расчетах коэффициентов модели, что показывают оценки параметров, вычисленных ОМНК.
Следовательно, диагональными элементами матрицы V можно усиливать или ослаблять влияние значений Х на отдельные значения У – поэтому этот метод получил название взвешенной регрессии.

(ОМНК) (модуль 2)
Можно существенно упростить расчеты по ОМНК

при выполнении следующих условий: если матрица V является симметрической и положительно определенной, то ее можно представить как произведение двух матриц
V = PP', так как Р-1VP-1' = 1, то V-1 = P-1'P-1 .
Если уравнение У=ХА+e умножить слева на матрицу P-1 , то получим
У*=Х*А+e*,
где У*=P-1У, Х*=Р-1Х, е*=Р-1е
В = (Х*'Х*)-1Х*'У* = (Х'V-1Х)-1 Х'V-1У
Вывод. Если исходные данные Х и У преобразовать:
У*=P-1У, Х*=Р-1Х,
то по преобразованным данным можно оценить параметры модели с помощью МНК, которые будут совпадать с оценками, вычисленными ОМНК.

(ОМНК) (модуль 2)
Если в диагональной матрице V (при

условии наличия гетероскедастичности и отсутствия автокорреляции) диагональными элементами взять квадраты остатков еi модели:
Уi = а0 + а1Хi +еi,
то, матрица Р-1 будет иметь следующий вид (при объеме выборки, равной пяти):

(ОМНК) (модуль 2)
Преобразования : У*=P-1У, Х*=Р-1Х, е*=Р-1е означают,

что все переменные, в том числе и переменная, равная 1, стоящая около свободного коэффициента, делятся на модуль остатков.
В скалярном выражении преобразованная модель будет иметь следующий вид:
Уi/|еi| = а0X0i/|еi| + а1Хi/|еi| +еi/|еi|.
В новой модели остатки будут принимать значения 1 или -1, т.е. будут гомоскедастичными, коэффициенты новой модели можно рассчитать МНК, остатки будут удовлетворять предпосылкам МНК. Коэффициенты, вычисленные по новой модели МНК являются оценками, вычисленные ОМНК.

(ОМНК) (модуль 2)
Полученная новая модель позволяет решить две

очень важные задачи в условиях гетероскедастичных остатков по исходной модели.
Первая задача. Если в исходной модели использовать коэффициенты, вычисленные ОМНК, то расчетные значения уравнения пройдут ближе к тем значениям, остатки которых будут наименьшими.
Вторая задача. Если расчетные значения Ур, доверительные интервалы уравнения регрессии, вычисленные по новой модели, умножить на |ei|, то мы перейдем к исходным значениям модели, в которой доверительные интервалы уравнения регрессии будут учитывать гетероскедастичность остатков.
Таким образом, ОМНК позволяет устранить гетреоскедастичность в новой модели и учитывать ее в исходной модели.

Возможны частные случаи, если дисперсии остатков пропорциональны квадрату значений Х: ϭi2 = Хi2 ϭ2 , то преобразованная модель будет иметь вид: Уi/Хi = а0Х0i/ Хi + а1Хi/Хi +еi/Хi,
в которой при определенных условиях новым переменным можно дать экономическую интерпретацию.
Например, У – издержки производства, Х – объем продукции, то новая переменная: У/Х – означает затраты на единицу продукции

(ОМНК) (модуль 2)
8.4. Использование ОМНК при наличии автокорреляции остатков

Рассмотрим более подробно второе условие: если матрица V имеет одинаковые диагональные элементы, не диагональные элементы расположены так, что определитель матрицы не равен нулю.
Данное условие означает, что гетероскедастичность отсутствует, но имеется автокорреляция остатков с определенными свойствами.
В эконометрической литературе имеются хорошо отработанные методы построения модели автокорреляции остатков первого порядка.
Представим уравнение модели в матричном виде:
У = ХА + е, et = ρet-1 + vt.

(ОМНК) (модуль 2)
Если возмущения появляются в результате использования

автокорреляционной схемы первого порядка et = ρet-1 + vt , при отсутствии гетероскедастичности, то
М(ее') = V = ϭ2Ω,
где






Обоснование структуры Ω см. Джонстон, 1980, стр. 242-244.
Матрица Ω является симметрической и положительно определенной, от которой можно получить обратную матрицу.

(ОМНК) (модуль 2)
Для того, чтобы оценки параметров модели,

при наличии нарушений предпосылки 4, были несмещенными, состоятельными и эффективными, можно использовать формулу обобщенного метода наименьших квадратов (метод Эйткена):



где В – вектор столбец коэффициентов модели, вычисленный по методу Эйткена;
Х – матрица значений факторов,
У – вектор столбец зависимой переменной,
Ω – матрица симметрическая, положительно определенная,
Ω -1 – обратная матрица от Ω.

(ОМНК) (модуль 2)
Если матрица Ω является симметрической и положительно определенной,

то возможно следующее соотношение:
Ω = PP,
где матрица Р является невырожденной.
Для модели автокорреляции остатков первого порядка расчет матрицы Р-1 упрощается.






Если модель У = ХА + е умножить слева на матрицу Р-1, получим следующие преобразованные значения исходных данных:

(ОМНК) (модуль 2)
Если модель У = ХА +

е умножить слева на матрицу Р-1, получим следующие преобразованные значения исходных данных




Коэффициенты ОМНК можно получить, если использовать МНК к новым преобразованным данным. (Джонстон 1980, стр.257-259).
Использование коэффициентов, определенных ОМНК в модели
У = ХА + е, et = ρet-1 + vt.
позволяет улучшить аппроксимацию исходных данных

(ОМНК) (модуль 2)
Однако для проведения расчетов необходимо знать

оценку коэффициента автокорреляции остатков первого порядка ρ.
В эконометрической литературе имеется несколько методов определения коэффициента автокорреляции остатков первого порядка, которые дают примерно одинаковые результаты.
Поэтому предлагаем самый простой метод определения коэффициента автокорреляции первого порядка, называемый методом наименьших квадратов, который выполняется в следующей последовательности:
Шаг 1. Вычисляются коэффициенты линейной модели с помощью функции ЛИНЕЙН.
Шаг 2. Вычисляются остатки модели е = У- (а0+а1*Х)
Шаг 3. Вычисляется коэффициент автокорреляции первого порядка r1 для остатков модели с помощью функции КОРРЕЛ, где первым массивом являются значения остатков еt, вторым массивом являются остатки модели, сдвинутые на одну дату времени еt-1.
Шаг 4. r1 является оценкой ρ.