Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторная и фрактальная графика
Содержание
- 1. Векторная и фрактальная графика
- 2. План:Основные понятия векторной графикиМатематические основы векторной графикиДостоинства и недостатки векторной графикиПрограммы векторной графики Фрактальная графика
- 3. Основные понятия векторной графикиБазовым элементов векторной графики
- 4. Основные понятия векторной графикиНапример, линия обладает следующими
- 5. Основные понятия векторной графикиВ векторной графики для
- 6. Математические основы векторной графикиТочка. Этот объект на
- 7. Математические основы векторной графикиПрямая линия. Ей соответствует
- 8. Математические основы векторной графикиКривая второго порядка. К
- 9. Математические основы векторной графикиКривая третьего порядка. Отличие
- 10. Математические основы векторной графики
- 11. Кривые БезьеСегмент кривой Безье третьего порядка описывается
- 12. Кривые БезьеМетод построения кривой Безье основан на
- 13. Достоинства и недостатки векторной графикиДостоинства векторной графики:простое
- 14. Достоинства и недостатки векторной графикиНедостатки векторной графики:
- 15. Программы векторной графикиCorelDrawAdobe Illustrator Macromedia FreeHand Deneba Canvas
- 16. Пример векторного и растрового изображения
- 17. Corel DrawОсновные возможности:Создание простых геометрических фигур, произвольных
- 18. Фрактальная графикаФрактал— объект, отдельные элементы которого наследуют
- 19. Сейчас исследование фракталов развивается по 2-м направлениям:фрактал
- 20. Основное свойство фракталов – самоподобие. Любой микроскопический
- 21. Фрактальная графикаБерем отрезок и среднюю его треть
- 22. Если на каждом шаге не только уменьшать
- 23. Базовым элементом фрактальной графики является сама математическая
- 24. Фрактальная графикаТаким способом строят как простейшие регулярные
- 25. Фрактальная графикаСнежинка Коха Лист
- 26. Треугольни Серпинского Фрактальная графика
- 27. Фрактальная графика
- 28. Фрактальная графика
- 29. Программы фрактальной графикиFractintManpwin
- 30. Скачать презентанцию
План:Основные понятия векторной графикиМатематические основы векторной графикиДостоинства и недостатки векторной графикиПрограммы векторной графики Фрактальная графика
Слайды и текст этой презентации
Слайд 2План:
Основные понятия векторной графики
Математические основы векторной графики
Достоинства и недостатки векторной
графики
Слайд 3Основные понятия векторной графики
Базовым элементов векторной графики является линия.
Векторная графика
представляет изображение как набор примитивов (элементарных объектов).
Примитивы: точки, прямые,
окружности, прямоугольники, а также как общий случай, сплайны некоторого порядка. Объектам присваиваются некоторые атрибуты, например, толщина линий, цвет заполнения. Рисунок хранится как набор координат, векторов и других чисел, характеризующих набор примитивов.
Слайд 4Основные понятия векторной графики
Например, линия обладает следующими свойств: формой (прямая,
кривая), толщиной, цветом, начертанием (сплошная, пунктирная).
Замкнутые линии приобретают свойство
заполнения. Охватываемое ими пространство может быть заполнено другими объектами (текстуры, карты) или выбранным цветом. Заполнение бывает растровым и векторным. Слайд 5Основные понятия векторной графики
В векторной графики для описания объектов используются
комбинации компьютерных команд и математических формул. Это позволяет устройствам при
рисовании вычислять, где необходимо поместить реальные точки.Слайд 6Математические основы векторной графики
Точка. Этот объект на плоскости представляется двумя
числами (x,y), указывающими его положение относительно начала координат.
Слайд 7Математические основы векторной графики
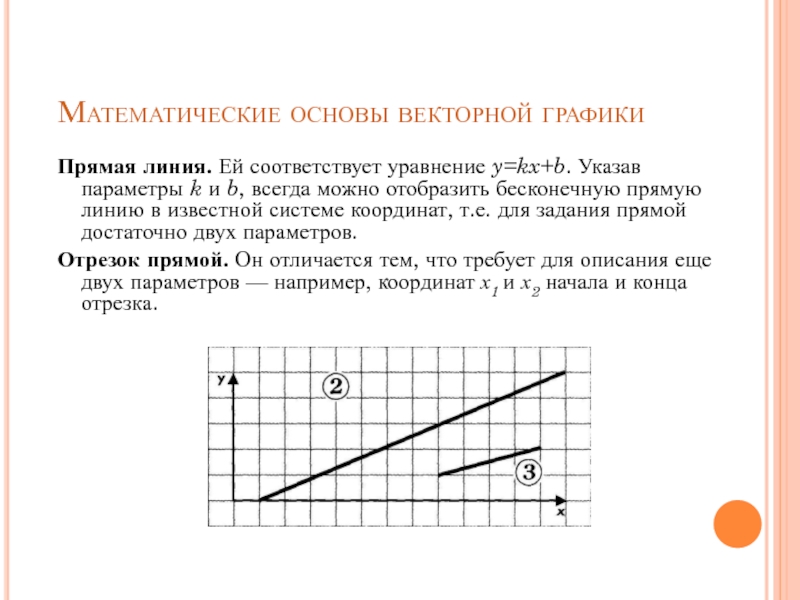
Прямая линия. Ей соответствует уравнение y=kx+b. Указав
параметры k и b, всегда можно отобразить бесконечную прямую линию
в известной системе координат, т.е. для задания прямой достаточно двух параметров.Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров — например, координат х1 и х2 начала и конца отрезка.
Слайд 8Математические основы векторной графики
Кривая второго порядка. К этому классу кривых
относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения
которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так:х2 + а1у2 + а2ху + а3х + а4у + а5 = 0
Таким образом, для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра
Слайд 9Математические основы векторной графики
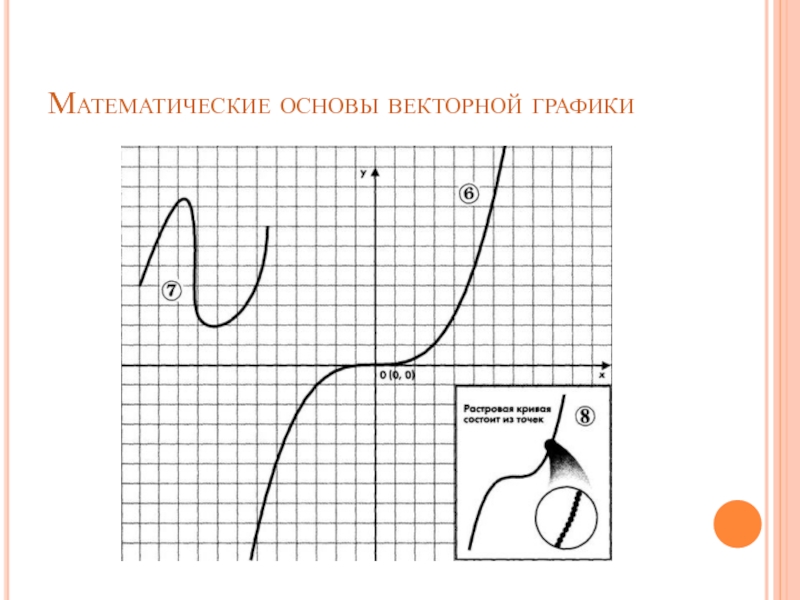
Кривая третьего порядка. Отличие этих кривых от
кривых второго порядка состоит в возможном наличии точки перегиба. Например,
график функции у = х3 имеет точку перегиба в начале координат. Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Все кривые второго порядка, в том числе прямые линии, являются частными случаями кривых третьего порядка.В общем случае уравнение кривой третьего порядка можно записать так:
х3 + а1у3 + а2х2у + а3ху2 + а4х2 + а5у2 + а6ху + а7х + а8у + а9 = 0
Таким образом, кривая третьего порядка описывается девятью параметрам. Описание ее отрезка потребует на два параметра больше.
Код описание кривой третьего порядка занимает в файле несравнимо меньше места, чем код аналогичной кривой, но созданной из точек (растровой).
Слайд 11Кривые Безье
Сегмент кривой Безье третьего порядка описывается положением четырех точек.
Две из них являются опорными (узлами кривой): начальная точка Р0(х0,
у0) и конечная точка Р3(х3, у3). Точки Р1(х1, у1) и Р2(х2, у2), определяющие положение касательных относительно отрезка, называют управляющими.Слайд 12Кривые Безье
Метод построения кривой Безье основан на использовании пары касательных
(управляющих линий), проведенных к сегменту кривой в его окончаниях. На
форму кривой влияют угол наклона касательной и длина ее отрезка.Слайд 13Достоинства и недостатки векторной графики
Достоинства векторной графики:
простое описание объекта, которое
занимает малое количество памяти
простата масштабирования, без ухудшения качества: масштабирование осуществляется
умножением параметров примитива на коэффициент умножениянезависимость объема памяти требуемой для хранения файла от выбранной цветовой модели.
Слайд 14Достоинства и недостатки векторной графики
Недостатки векторной графики:
некоторая искусственность –
любое изображение необходимо разбить на конечное множество составляющих его примитивов.
внешнее
представление векторных изображений может изменяться в зависимости от отображающей их программы.векторные данные плохо отображаются на растровых устройствах вывода.
Векторная графика хорошо подходит для чертежей и изображений с простыми формами, тенями и окрасками.
Слайд 17Corel Draw
Основные возможности:
Создание простых геометрических фигур, произвольных кривых и ломаных,
замкнутых и разомкнутых.
Вставка и форматирование текста.
Редактирование любого объекта:
изменение цвета контура и заливки, изменение формы объекта. Вставка готовых картинок или ранее созданных вами иллюстраций в документ.
Применение разнообразных художественных эффектов.
Размещение всех объектов в нужных местах, определение порядка взаимного перекрытия объектов.
Создание многостраничных документов;
Средства работы с растровыми объектами.
Слайд 18Фрактальная графика
Фрактал— объект, отдельные элементы которого наследуют свойства родительских структур.
Фрактальными свойствами обладают многие природные объекты, такие как снежинка, кристаллы,
растения.Фрактал —это некое преобразование многократно примененное к исходной фигуре.
Слайд 19Сейчас исследование фракталов развивается по 2-м направлениям:
фрактал – наилучшее направление
живой природы
фрактал как способ сжатия информации
Фрактальная геометрия появилась в конце
70-х годов.Слово фрактал образовано от латинского fractus – состоящий из фрагментов. Термин фрактал предложил Бенуа Мандельброт. По его определению фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.
Фрактальная графика
Слайд 20Основное свойство фракталов – самоподобие. Любой микроскопический фрагмент фрактала в
том или ином отношении воспроизводит его глобальную структуру.
В простейшем
случае часть фрактала представляет собой просто уменьшенный целый фрактал.Фрактальная графика
Слайд 21Фрактальная графика
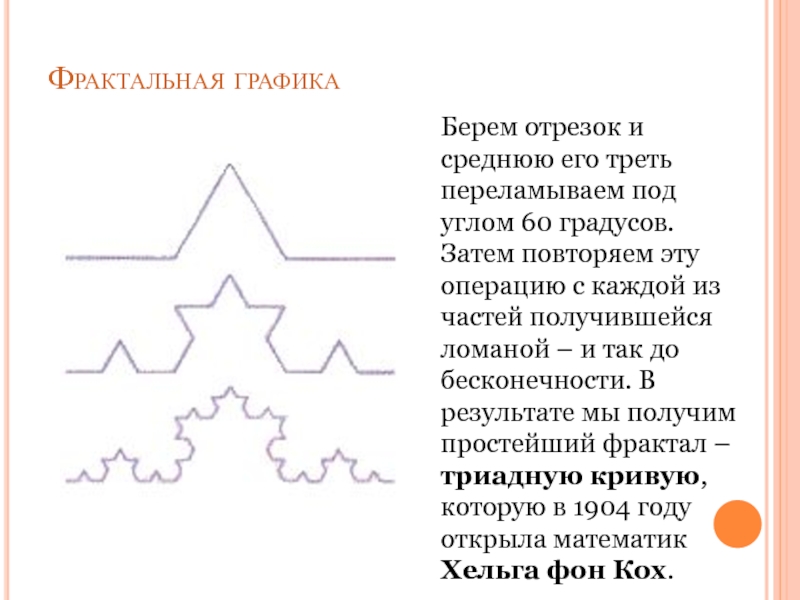
Берем отрезок и среднюю его треть переламываем под углом
60 градусов. Затем повторяем эту операцию с каждой из частей
получившейся ломаной – и так до бесконечности. В результате мы получим простейший фрактал – триадную кривую, которую в 1904 году открыла математик Хельга фон Кох.Слайд 22Если на каждом шаге не только уменьшать основной мотив, но
также смещать и поворачивать его, можно получить более интересные и
реалистически выглядящие образования, например, лист папоротника или даже целые их заросли. А можно построить весьма правдоподобный фрактальный рельеф местности и покрыть её лесом.Фрактальная графика
Слайд 23Базовым элементом фрактальной графики является сама математическая формула, то есть
никаких объектов в памяти компьютера не хранится и изображение строится
исключительно по уравнениям.Отдельные элементы фрактальной структуры математически описываются также как и объект в целом.
Фрактальная графика