Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве
Содержание
- 1. Векторы в пространстве
- 2. План изучения темыВспомним планиметрию «Векторы на плоскости»«Векторы в пространстве»
- 3. Тезаурус по теме «Векторы на
- 4. Понятие вектораВектор – направленный отрезокА – начало вектора В – конец вектораОбозначение: ВА
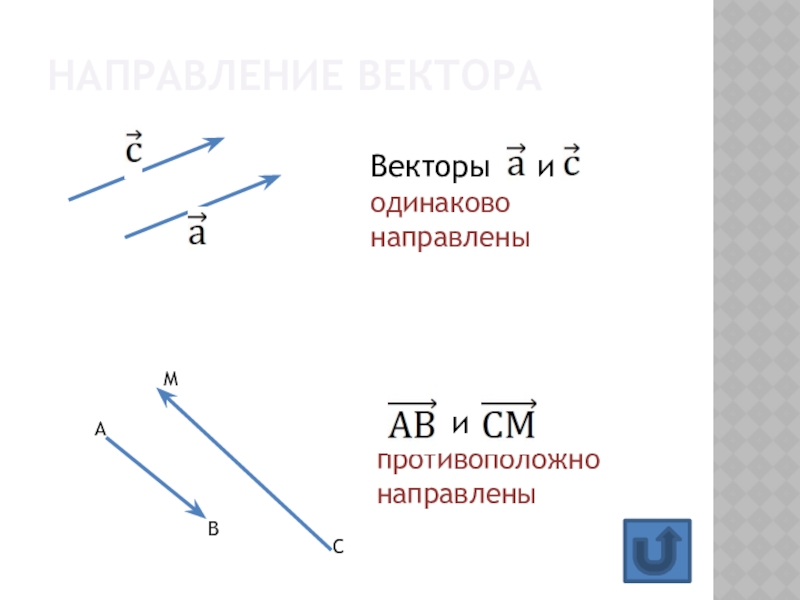
- 5. Направление вектора ВА и противоположно направленыВекторы и одинаково направленыСМ
- 6. Равные векторы Два вектора называются равными, если
- 7. Коллинеарные вектораКоллинеарные вектора сонаправлены и лежат на
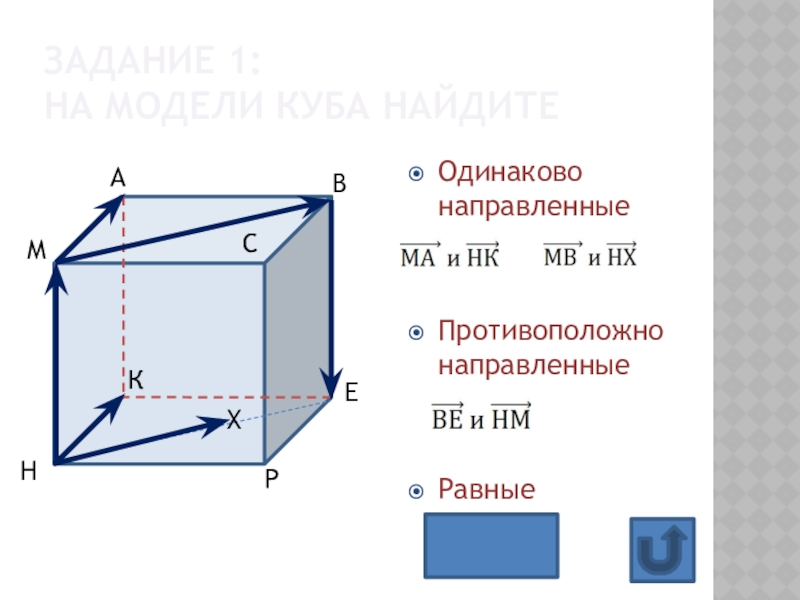
- 8. Одинаково направленныеПротивоположно направленныеРавные Задание 1: на модели куба найдитеХ
- 9. Абсолютная величина вектора Нулевой вектор – вектор,
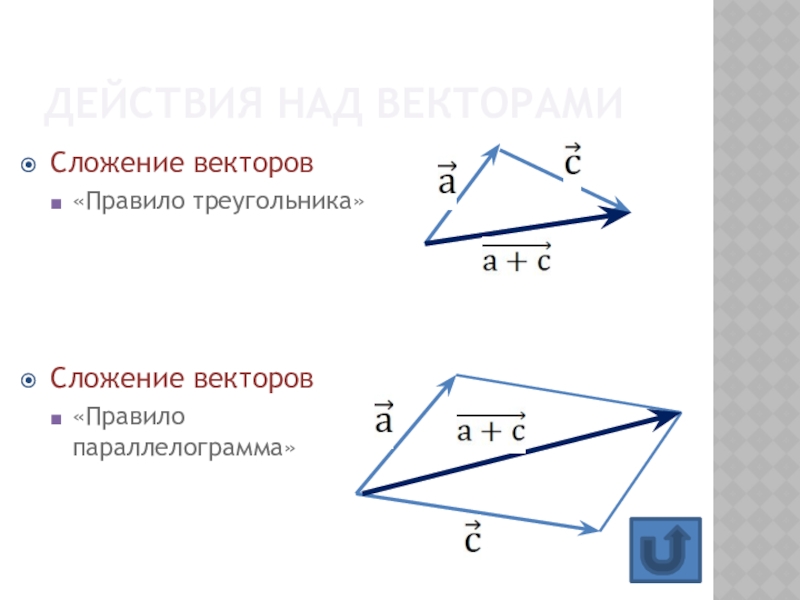
- 10. Действия над векторамиСложение векторов«Правило треугольника»Сложение векторов«Правило параллелограмма»
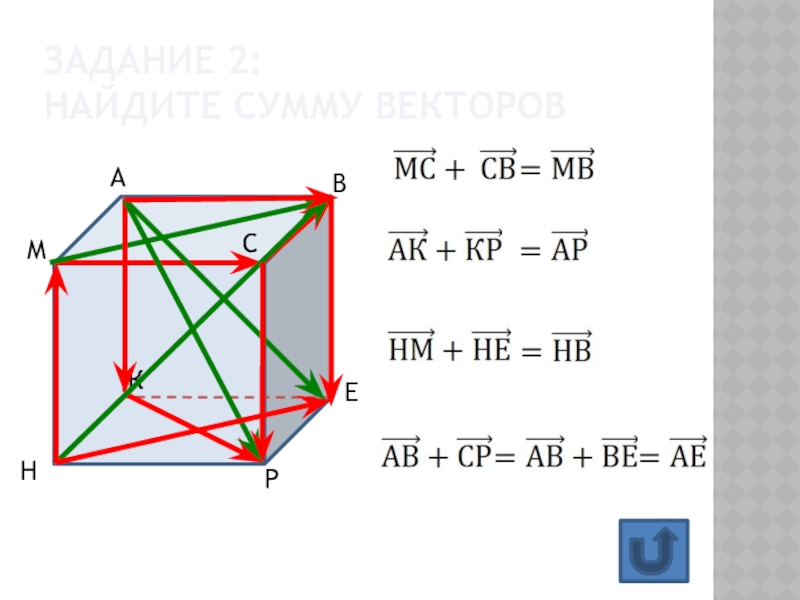
- 11. Задание 2: найдите сумму векторов
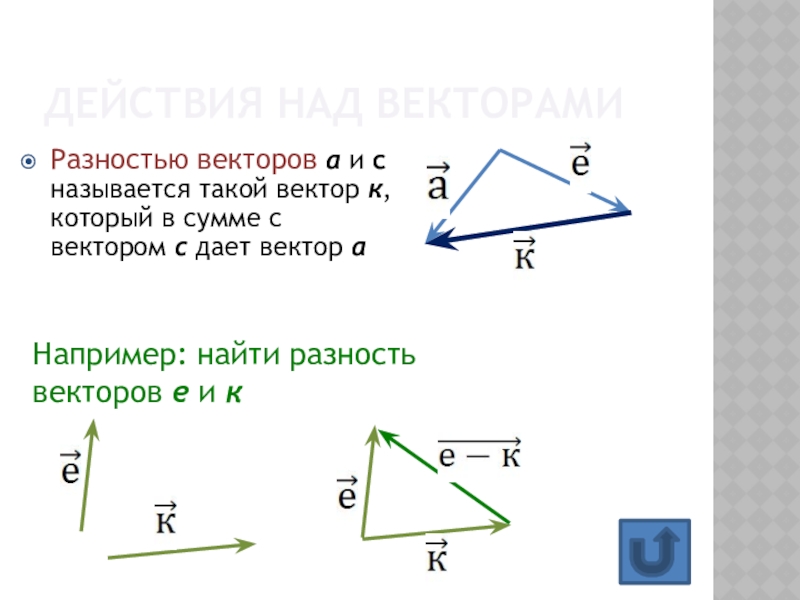
- 12. Действия над векторамиРазностью векторов а и с
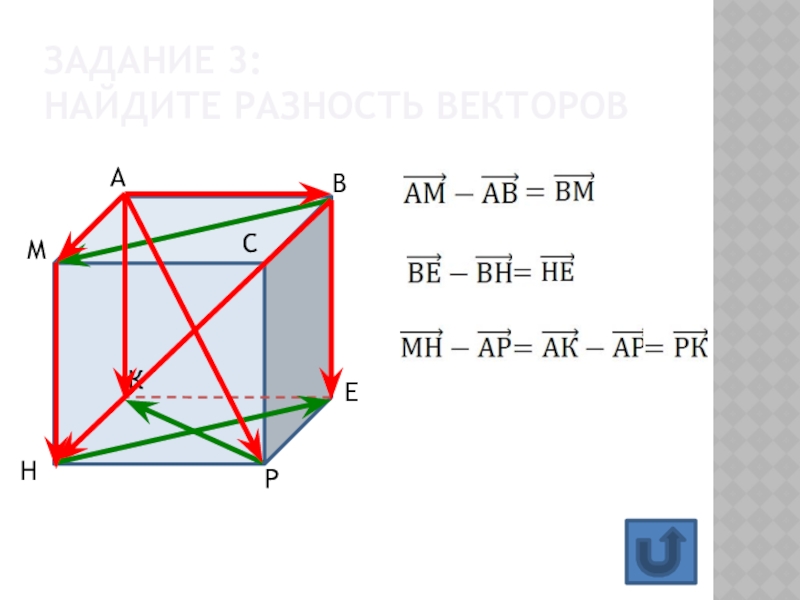
- 13. Задание 3: найдите разность векторов
- 14. тема «Векторы в пространстве»Вектор, направление, абсолютная
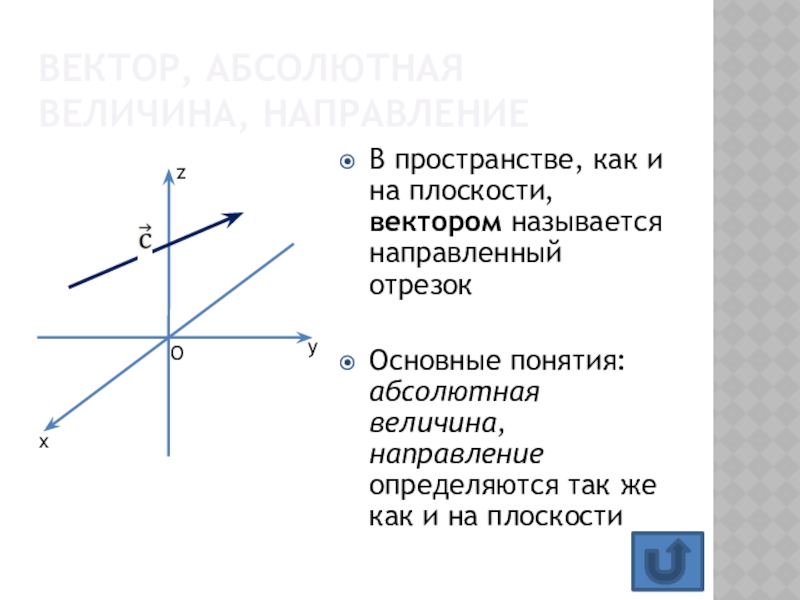
- 15. В пространстве, как и на плоскости, вектором
- 16. Координаты вектораА(х1;у1;z1) B(x2;y2;z2) (x2-х1;y2-у1;z2-z1)Пример:определить
- 17. Равные векторыАВРавные векторы имеют равные соответствующие координаты
- 18. Задание 4: укажите пары равных векторовДано:
- 19. Суммой векторов (а;b;с) и (m;n;k)
- 20. Произведением вектора (а;в;с) на число λ
- 21. Скалярным произведением векторов (а;в;с) и
- 22. Задание 5: выполните действия над векторами в пространствеДано:Найти:
- 23. Использовалось учебное пособие автора Погорелова А.П. «Геометрия
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3 Тезаурус по теме
«Векторы на плоскости»
Понятие вектора
Направление вектора
Равные векторы
Коллинеарные
вектора
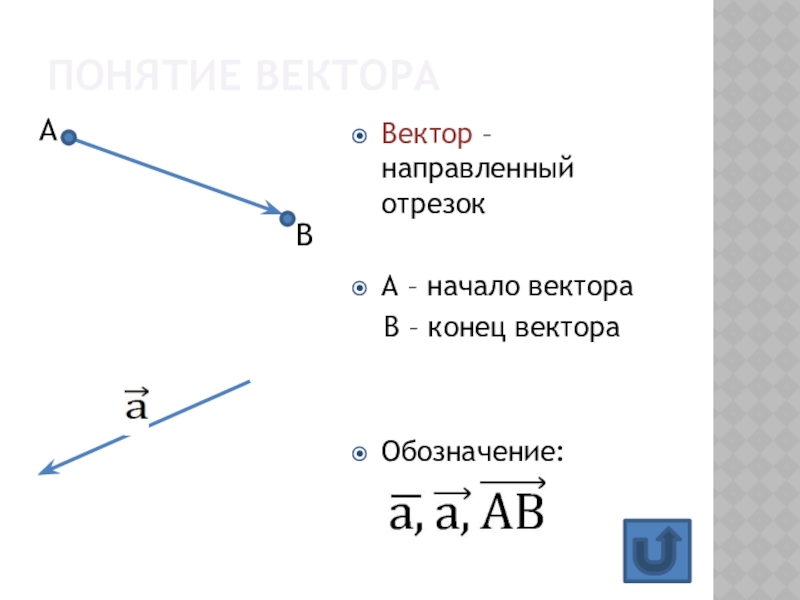
Слайд 4Понятие вектора
Вектор – направленный отрезок
А – начало вектора
В
– конец вектора
Обозначение:
В
А
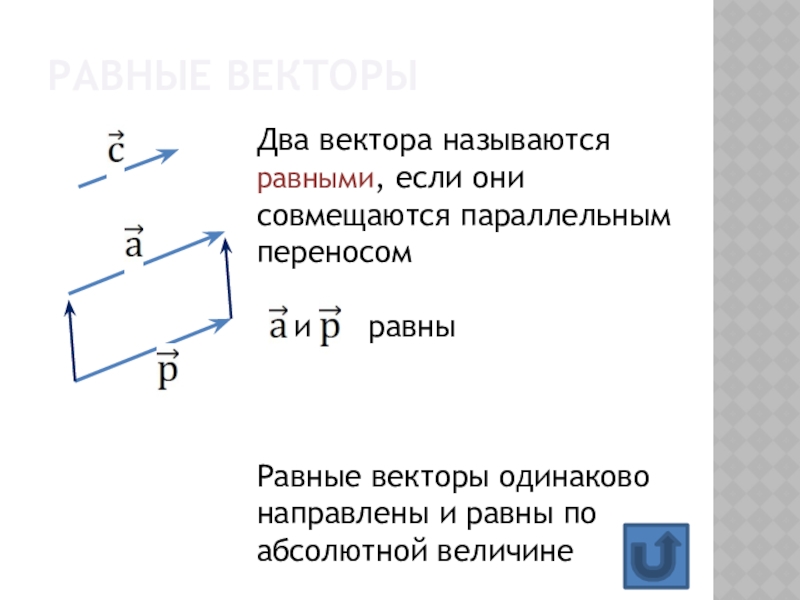
Слайд 6Равные векторы
Два вектора называются равными, если они совмещаются параллельным
переносом
и равны
Равные векторы одинаково направлены
и равны по абсолютной величинеСлайд 7Коллинеарные вектора
Коллинеарные вектора сонаправлены и лежат на параллельных прямых или
на одной.
, , - коллинеарные
=λ∙ е
у
Слайд 9Абсолютная величина вектора
Нулевой вектор – вектор, у которого начало
совпадает с его концом
Абсолютная величина (или модуль) вектора – длина
отрезка, изображающего векторОбозначение:
Слайд 10Действия над векторами
Сложение векторов
«Правило треугольника»
Сложение векторов
«Правило параллелограмма»
Слайд 12Действия над векторами
Разностью векторов а и с называется такой вектор
к, который в сумме с вектором с дает вектор а
Например:
найти разность векторов е и кСлайд 14тема
«Векторы в пространстве»
Вектор, направление, абсолютная величина
Координаты вектора в пространстве
Равные
вектора
Сложение векторов в пространстве
Умножение вектора на число
Скалярное произведение векторов
Задание 4
Задание
5Слайд 15В пространстве, как и на плоскости, вектором называется направленный отрезок
Основные
понятия: абсолютная величина, направление определяются так же как и на
плоскостиВектор, абсолютная величина, направление
z
x
y
O
Слайд 16Координаты вектора
А(х1;у1;z1) B(x2;y2;z2)
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
,
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))(-14;1;5)
Координаты вектора в пространстве
А
В
Слайд 17Равные векторы
А
В
Равные векторы имеют равные соответствующие координаты
(х;y;z) (a;b;c)
Если х=а,у=b, z=с, то
= С
М
Слайд 18Задание 4:
укажите пары равных векторов
Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов
Решение:
Равны соответствующие координаты
у векторов , , значит, они
попарно равны
Слайд 19Суммой векторов (а;b;с) и (m;n;k) называется вектор
(a+m;b+n;c+k)
Например, найти координаты вектора
,если (-5;3;-9) и (4; -2; 8)
Решение:
(-5+4; 3+(-2); -9+8)
(-1; 1; 1)
Сложение векторов в пространстве
Слайд 20Произведением вектора (а;в;с) на число λ называется вектор λ
(λа; λв; λс)
Например, найти координаты вектора ,
если (5;-1;-2)Решение:
Умножение вектора на число
Слайд 21Скалярным произведением векторов (а;в;с) и (х;у;z) называется
число =ax+вy+cz
Например,
найти скалярное
произведение векторов и
Решение:
Скалярное произведение векторов в пространстве
Слайд 23Использовалось учебное пособие автора Погорелова А.П. «Геометрия 10-11». Учебник для
общеобразовательных учреждений, М: Просвещение, 2009.
Из данного учебного пособия
заимствованы рассматриваемые в работе понятия Все рисунки и задачи авторские