Волны

Содержание

1. Волны
2. Волна – процесс распространения колебаний пространстве. МеханикаВолна
3. Рассмотрим поперечную волну, распространяющуюся в однородной, изотропной
4. Плоская волна.Ф.В. В.П.SисточникСферическая волна.SВ.П.Ф.В. Фронт волны –
5. АУравнение бегущей волны
6. Волновое числоУравнение бегущей волныСимметричная форма записи Подчёркивает периодичность во времени и пространстве
7. Ур-ие плоской бегущей волны, распространяющейся в направлении
8. Уравнение ДаламбераДифференциальное ур-е свободных колебанийУр-е свободных колебаний
9. уравнение бегущей волныНайдём, решением какого диф. ур-я
10. Уравнение ДаламбераПродольные волны в твёрдой среде:Относительное удлинение (сжатие)Модуль ЮнгаУпругая силаПлощадь сечения (стержня)Поперечные волны в твёрдой среде:
11. Уравнение ДаламбераГаз и жидкость – нет упругого
12. Потенц.энергия упругой деформации пружины- З-н ГукаПотенциальная энергия упругой деформацииПотенц.энергия упругой деформации стержняЭнергия. Плотность энергии упругой волны.
13. Полная энергия:Энергия. Плотность энергии упругой волны.Рассмотрим плоскую
14. Плотность энергии упругой волныУсредненное по времени значение.Средняя
15. 0z
16. Плотность потока энергии ( Вектор Умова). Поток энергии.
17. Зависимость амплитуды сферической волны от расстояния от
18. Интерференция волнЕсли от источника колебаний волны доходят
19. Приёмник под воздействием одной первой волны совершал
20. Аналогично, для интерференционного ослабления необходимо:Таким образом:Интерференционное усиление
21. Все точки вдоль z колеблются в одной
22. Слайд 22
23. Скачать презентанцию

Волна – процесс распространения колебаний пространстве. МеханикаВолна – процесс распространения колебаний в упругой среде (твёрдой, жидкой и газообразной).Если в каком либо месте упругой среды возбудить колебания её частиц, то колебание станет

Слайды и текст этой презентации

Слайд 1Волны
Характеристики волн. Типы волн. Уравнение бегущей волны. Стоячие волны.

Слайд 2Волна – процесс распространения колебаний пространстве.
Механика
Волна – процесс распространения

колебаний в упругой среде (твёрдой, жидкой и газообразной).
Если в каком

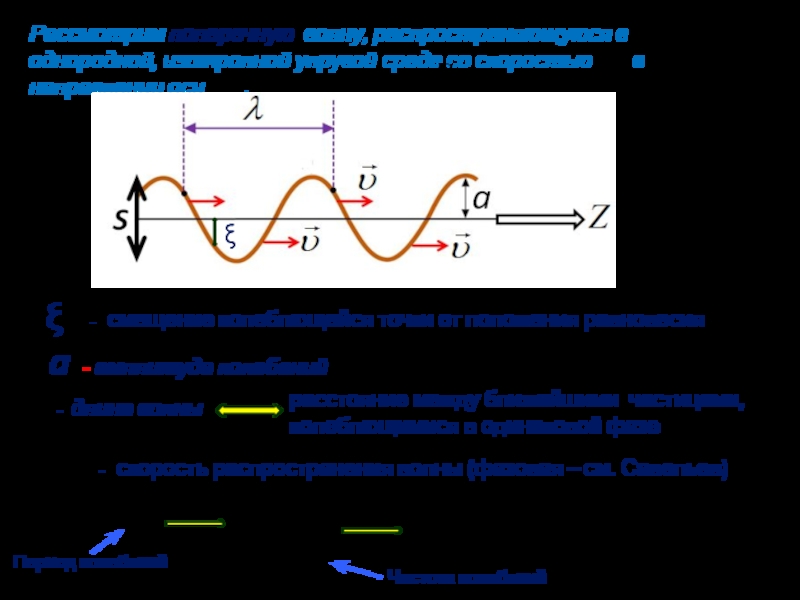
либо месте упругой среды возбудить колебания её частиц, то колебание станет распространяться от частицы к частице с некоторой скоростью v.

Частицы среды совершают колебания около своих положений равновесия и не переносятся волной.

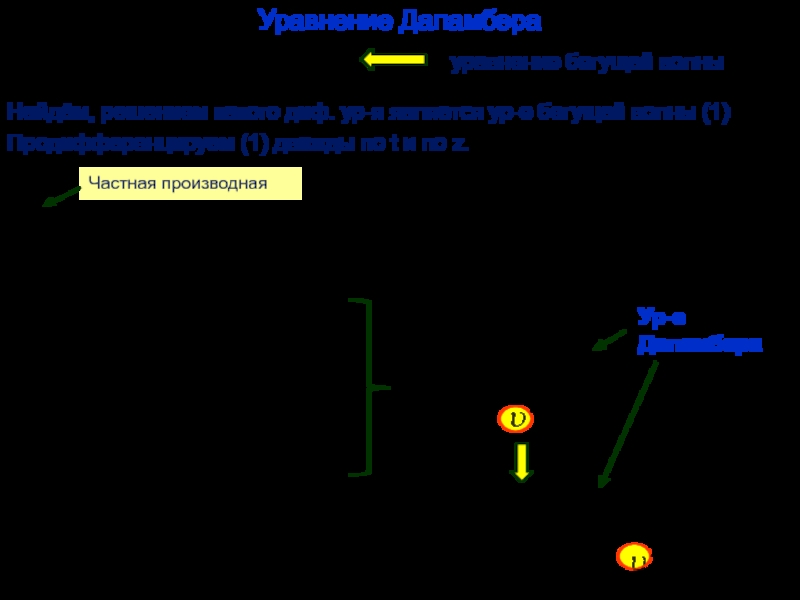
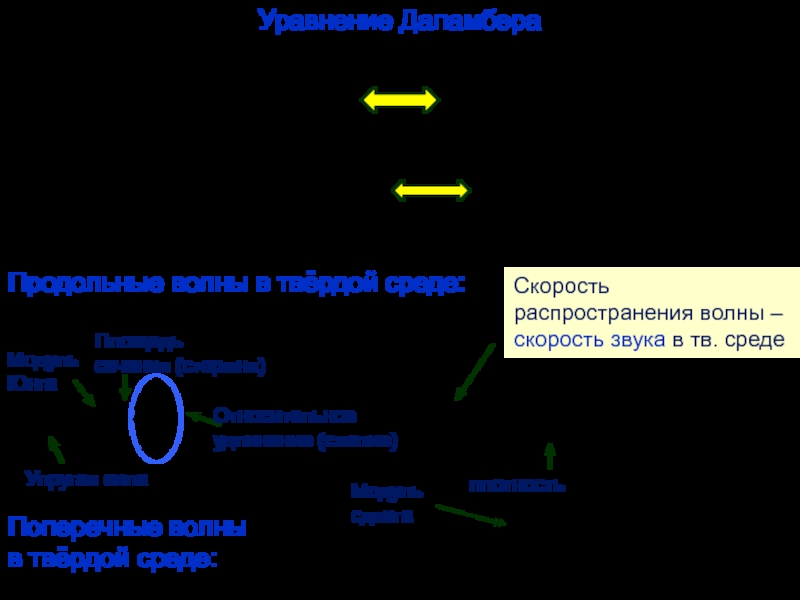
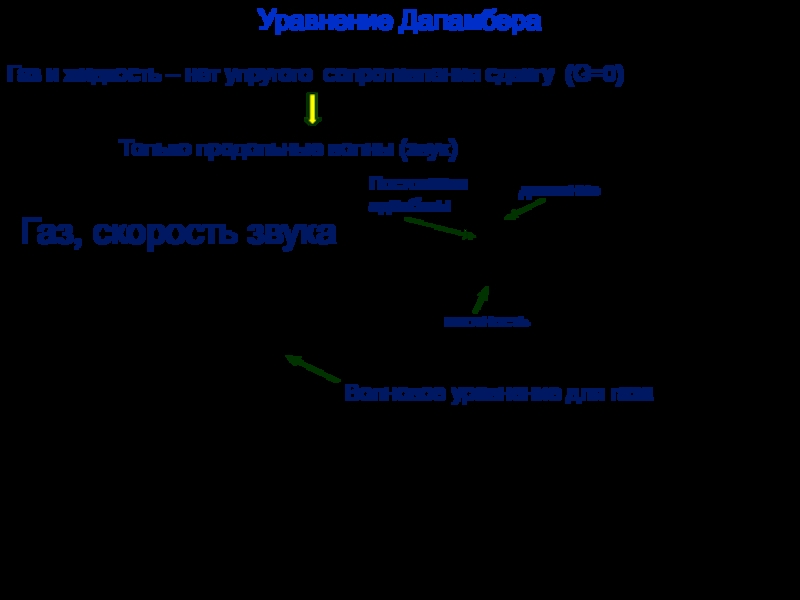
Продольные волны – направление колебаний вдоль направления распространения волны (любая упругая среда: твёрдая, жидкая газообразная).

Поперечные волны – направление колебаний перпендикулярно направлению распространения волны: электромагнитные волны, твёрдое тело (сопротивление деформации сдвига).

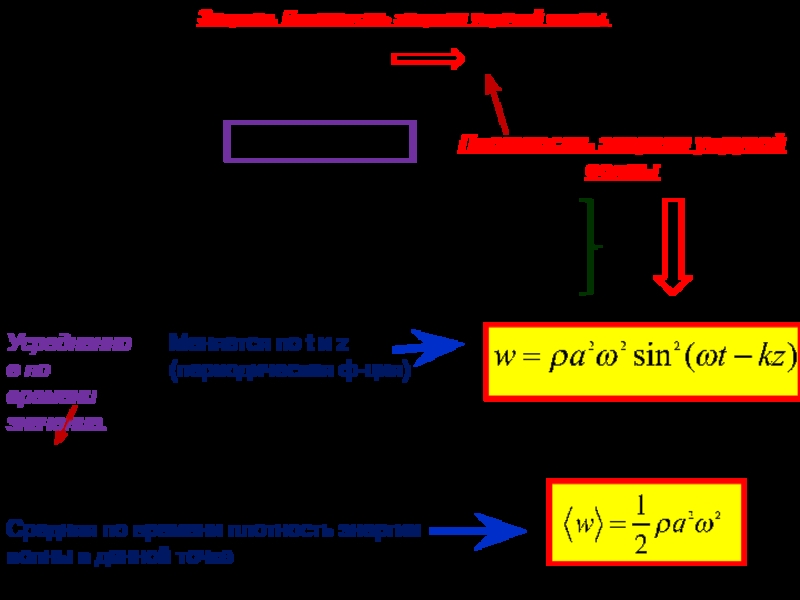
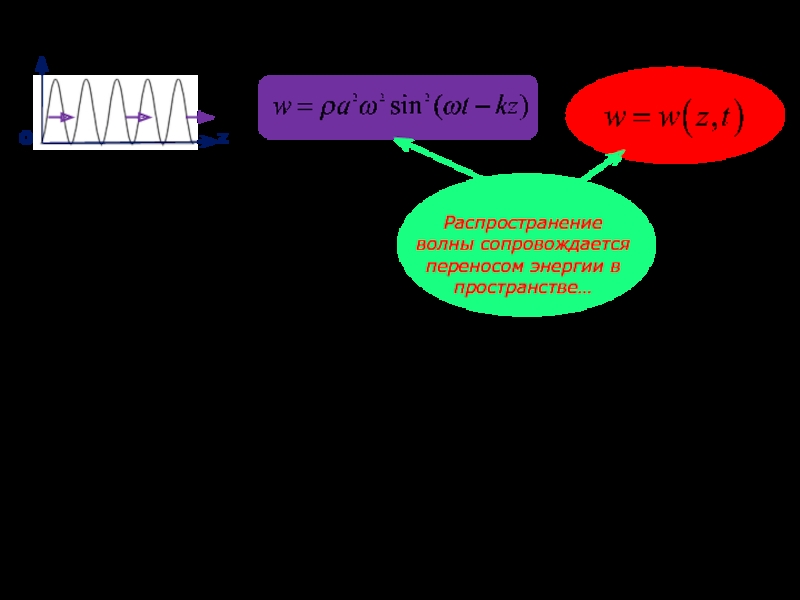
Процесс – периодический не только во времени, но и в пространстве

Волна – процесс распространения колебаний пространстве. МеханикаВолна – процесс распространения колебаний в упругой среде (твёрдой, жидкой и

Слайд 3Рассмотрим поперечную волну, распространяющуюся в однородной, изотропной упругой среде со

скоростью в направлении оси

a - амплитуда колебаний

- скорость распространения волны (фазовая – см. Савельев)

Период колебаний

Частота колебаний

Рассмотрим поперечную волну, распространяющуюся в однородной, изотропной упругой среде со скоростью в направлении оси

Слайд 4Плоская волна.
Ф.В.
В.П.
S
источник
Сферическая волна.
S
В.П.
Ф.В.
Фронт волны – геометрическое место точек,

до которого дошли колебания на данный момент Ф.В.

Волновые поверхности – геометрическое место точек колеблющихся в одинаковой фазе В.П.

Плоская волна.Ф.В. В.П.SисточникСферическая волна.SВ.П.Ф.В. Фронт волны – геометрическое место точек, до которого дошли колебания на данный момент

Слайд 5А
Уравнение бегущей волны

Слайд 6Волновое число
Уравнение бегущей волны
Симметричная форма записи
Подчёркивает периодичность во времени

и пространстве

Слайд 7Ур-ие плоской бегущей волны, распространяющейся в направлении оси Z.
Ур-ие cферической

бегущей волны, распространяющейся в направлении луча r .
Ур-ие плоской бегущей

волны, распространяющейся в противоположном оси Z направлении .

Без учета затухания

Ур-ие плоской бегущей волны, распространяющейся в направлении оси Z.Ур-ие cферической бегущей волны, распространяющейся в направлении луча r

Слайд 8Уравнение Даламбера
Дифференциальное ур-е свободных колебаний
Ур-е свободных колебаний - решение диф.

ур-я свободных колебаний
Найдём, решением какого диф. ур-я является ур-е бегущей

волны (1) ??

Уравнение ДаламбераДифференциальное ур-е свободных колебанийУр-е свободных колебаний - решение диф. ур-я свободных колебанийНайдём, решением какого диф. ур-я

Слайд 9уравнение бегущей волны
Найдём, решением какого диф. ур-я является ур-е бегущей

волны (1)
Продифференцируем (1) дважды по t и по z.
Частная

производная

Ур-е Даламбера

Уравнение Даламбера

уравнение бегущей волныНайдём, решением какого диф. ур-я является ур-е бегущей волны (1)Продифференцируем (1) дважды по t и

Слайд 10Уравнение Даламбера
Продольные волны в твёрдой среде:
Относительное
удлинение (сжатие)
Модуль
Юнга
Упругая сила
Площадь

сечения (стержня)
Поперечные волны
в твёрдой среде:

Уравнение ДаламбераПродольные волны в твёрдой среде:Относительное удлинение (сжатие)Модуль ЮнгаУпругая силаПлощадь сечения (стержня)Поперечные волны в твёрдой среде:

Слайд 11Уравнение Даламбера
Газ и жидкость – нет упругого сопротивления сдвигу (G=0)

Только продольные волны (звук)
Газ, скорость звука
давление
Постоянная адиабаты
плотность
Волновое уравнение для газа

Уравнение ДаламбераГаз и жидкость – нет упругого сопротивления сдвигу (G=0) Только продольные волны (звук)Газ, скорость звукадавлениеПостоянная адиабатыплотностьВолновое

Слайд 12Потенц.энергия упругой деформации пружины
- З-н Гука
Потенциальная энергия упругой деформации
Потенц.энергия упругой

деформации стержня
Энергия. Плотность энергии упругой волны.

Потенц.энергия упругой деформации пружины- З-н ГукаПотенциальная энергия упругой деформацииПотенц.энергия упругой деформации стержняЭнергия. Плотность энергии упругой волны.

Слайд 13Полная энергия:
Энергия. Плотность энергии упругой волны.
Рассмотрим плоскую продольную волну,

распространяющуюся в однород., изотроп., упругой среде вдоль оси Z
Физически

малый объем (Δz<<λ)
в виде прямого цилиндра

Полная энергия:Энергия. Плотность энергии упругой волны.Рассмотрим плоскую продольную волну, распространяющуюся в однород., изотроп., упругой среде вдоль

Слайд 14Плотность энергии упругой волны
Усредненное по времени значение.
Средняя по времени плотность

энергии волны в данной точке
Энергия. Плотность энергии упругой волны.

Плотность энергии упругой волныУсредненное по времени значение.Средняя по времени плотность энергии волны в данной точке Энергия. Плотность

Слайд 150
z

Слайд 16Плотность потока энергии ( Вектор Умова).
Поток энергии.

Слайд 17Зависимость амплитуды сферической волны от расстояния от источника колебаний.
В случае

точечного ист-ка колебаний для однородной, изотропной среды:
По закону сохр. энергии:
Средний

по времени поток энергии

Зависимость амплитуды сферической волны от расстояния от источника колебаний.В случае точечного ист-ка колебаний для однородной, изотропной среды:По

Слайд 18Интерференция волн
Если от источника колебаний волны доходят до приёмника двумя

различными путями, то приёмник будет колебаться под одновременным воздействием обеих

волн  будет иметь место сложение колебаний одинаковых частот.
При одинаковых направлениях слагаемых колебаний амплитуда и энергия результирующего колебания:

При сложении одинаково направленных колебаний равных частот энергия результирующего колебания не равна сумме энергий слагаемых колебаний, совершающихся порознь

Интерференция волн – усиление или ослабление энергии результирующего колебания в зависимости от разности фаз слагаемых колебаний

При сложении взаимно перпендикулярных колебаний интерференции нет, т.к. при любых энергия

Интерференция волнЕсли от источника колебаний волны доходят до приёмника двумя различными путями, то приёмник будет колебаться под

Слайд 19Приёмник под воздействием одной первой волны совершал бы колебания, следующие

уравнению:
a под воздействием второй волны – уравнению
Разность фаз колебаний приёмника

под воздействием одного и другого колебаний:

Разность расстояний , которые проходят волны от источников до приёмника, называется разностью хода волн

Интерференционное усиление, согласно (1), имеет место при условии

отсюда

Приёмник под воздействием одной первой волны совершал бы колебания, следующие уравнению:a под воздействием второй волны – уравнениюРазность

Слайд 20Аналогично, для интерференционного ослабления необходимо:
Таким образом:
Интерференционное усиление имеет место, если

разность хода лучей равна целому числу длин волн или чётному

числу длин полуволн
Интерференционное ослабление имеет место, если разность хода лучей равна нечётному числу длин полуволн

Аналогично, для интерференционного ослабления необходимо:Таким образом:Интерференционное усиление имеет место, если разность хода лучей равна целому числу длин

Слайд 21Все точки вдоль z колеблются в одной фазе (фаза не

бежит – стоячая волна).
Амплитуда изменяется по периодическому закону вдоль z

Все точки вдоль z колеблются в одной фазе (фаза не бежит – стоячая волна).Амплитуда изменяется по периодическому

Слайд 22

Скачать презентацию

Разделы презентаций

Волны

Содержание

Слайды и текст этой презентации

Слайд 1ВолныХарактеристики волн. Типы волн. Уравнение бегущей волны. Стоячие волны.

Слайд 2Волна – процесс распространения колебаний пространстве. МеханикаВолна – процесс распространения

колебаний в упругой среде (твёрдой, жидкой и газообразной).Если в каком

Слайд 3Рассмотрим поперечную волну, распространяющуюся в однородной, изотропной упругой среде со

скоростью в направлении оси

Слайд 4Плоская волна.Ф.В. В.П.SисточникСферическая волна.SВ.П.Ф.В. Фронт волны – геометрическое место точек,

до которого дошли колебания на данный момент Ф.В.

Слайд 5АУравнение бегущей волны

Слайд 6Волновое числоУравнение бегущей волныСимметричная форма записи Подчёркивает периодичность во времени

и пространстве

Слайд 7Ур-ие плоской бегущей волны, распространяющейся в направлении оси Z.Ур-ие cферической

бегущей волны, распространяющейся в направлении луча r .Ур-ие плоской бегущей

Слайд 8Уравнение ДаламбераДифференциальное ур-е свободных колебанийУр-е свободных колебаний - решение диф.

ур-я свободных колебанийНайдём, решением какого диф. ур-я является ур-е бегущей

Слайд 9уравнение бегущей волныНайдём, решением какого диф. ур-я является ур-е бегущей

волны (1)Продифференцируем (1) дважды по t и по z. Частная

Слайд 10Уравнение ДаламбераПродольные волны в твёрдой среде:Относительное удлинение (сжатие)Модуль ЮнгаУпругая силаПлощадь

сечения (стержня)Поперечные волны в твёрдой среде:

Слайд 11Уравнение ДаламбераГаз и жидкость – нет упругого сопротивления сдвигу (G=0)

Только продольные волны (звук)Газ, скорость звукадавлениеПостоянная адиабатыплотностьВолновое уравнение для газа

Слайд 12Потенц.энергия упругой деформации пружины- З-н ГукаПотенциальная энергия упругой деформацииПотенц.энергия упругой

деформации стержняЭнергия. Плотность энергии упругой волны.

Слайд 13Полная энергия:Энергия. Плотность энергии упругой волны.Рассмотрим плоскую продольную волну,

распространяющуюся в однород., изотроп., упругой среде вдоль оси Z Физически

Слайд 14Плотность энергии упругой волныУсредненное по времени значение.Средняя по времени плотность

энергии волны в данной точке Энергия. Плотность энергии упругой волны.

Слайд 150z

Слайд 16Плотность потока энергии ( Вектор Умова). Поток энергии.

Слайд 17Зависимость амплитуды сферической волны от расстояния от источника колебаний.В случае

точечного ист-ка колебаний для однородной, изотропной среды:По закону сохр. энергии:Средний

Слайд 18Интерференция волнЕсли от источника колебаний волны доходят до приёмника двумя