Слайд 1Вторичная математическая обработка данных
Слайд 2Выбор статистического метода и классификация исследовательских задач
В целом в студенческих
работах можно выделить несколько групп задач, которые наиболее часто решаются
в экспериментальных исследованиях:
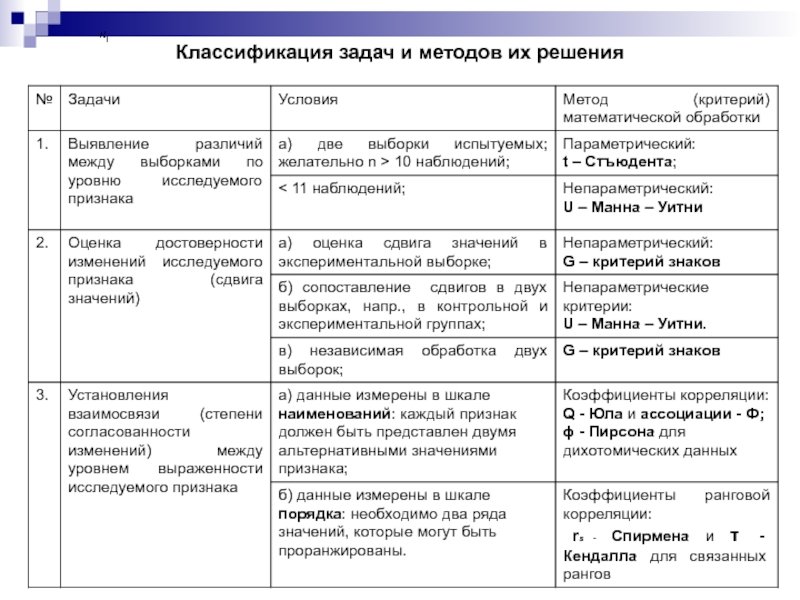
1. Выявление сходства или различия в уровне исследуемого признака.
2. Оценка сдвига значений исследуемого признака.
3. Выявление степени согласованности изменений признаков.
Слайд 3Классификация задач и методов их решения
Слайд 4Рекомендации к выбору критерия.
Необходимо определить, является ли выборка зависимой
или независимой.
Следует знать объём каждой выборки, её однородность –
неоднородность, нормальность распределения признака в ней.
При выборе критерия необходимо знать его ограничения. Начинать обработку лучше с наименее трудоёмкого метода; если он не позволил установить различия, следует применить другой – более мощный.
Следует помнить, что при малых объёмах выборки многие критерии становятся чувствительными к форме распределения признака и при этом необходимо увеличивать величину уровня значимости не менее 1 %, чтобы не принять ошибочное решение.
Слайд 5Выявление различий между выборками. Параметрические статистические критерии. t – Стъюдента
(критерий Госсета).
Основными параметрами критерия являются дисперсия ( ) и
среднее арифметическое значение (М).
Критерий даёт информацию о том, достоверно ли различие средних значений двух выборок, но данные должны соответствовать закону нормального распределения.
Если объём выборки меньше 10 наблюдений, лучше прибегнуть к непараметрическим критериям.
После его применения можно говорить о том:
удался эксперимент, оказал ли он влияние на уровень развития изучаемого признака (при этом замеры признака в одной и той же выборке делают в начале и в конце экспериментального исследования)
различаются ли группа А и группа В по выраженности изучаемого признака.
Слайд 6Параметрические статистические критерии. t – Стъюдента (критерий Госсета).
Алгоритм нахождения t
критерия:
1. Находим и ;
2.
Находим величины их статистических ошибок по формуле:
3. Находим (эмпирическое значение t – критерия) по формуле:
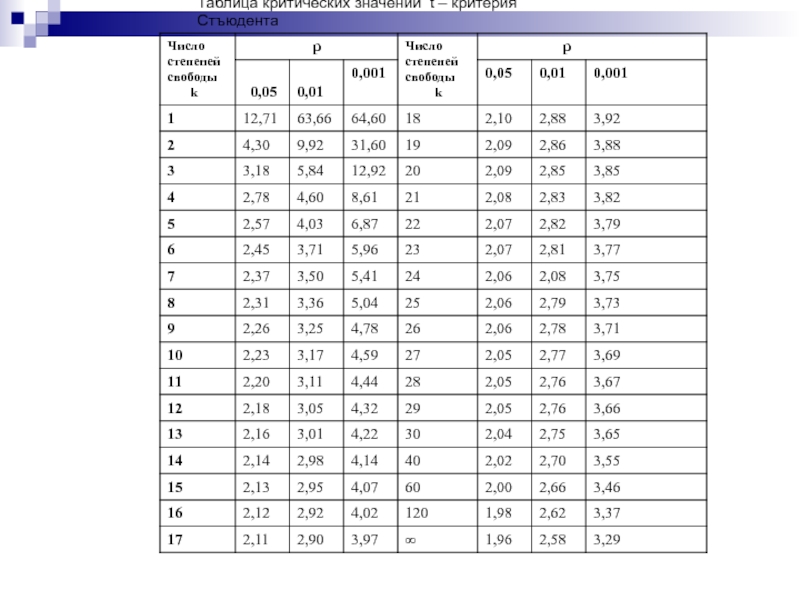
4. Находим (критическое значение) по таблице для 95% и 99% уровня значимости. р < 0,05 и р <0,01, для этого находим число степеней свободы по формуле: , где n – объёмы сравниваемых выборок.
Слайд 7Параметрические статистические критерии. t – Стъюдента (критерий Госсета).
Сравниваем
и
, делаем выводы, если эмпирическое значение превышает критические (табличные) для р<0,01, то различия статистически достоверны.
Слайд 8Таблица критических значений t – критерия Стъюдента
Слайд 9Непараметрические критерий U – Манна – Уитни
предназначен для оценки различий
между двумя выборками по уровню выраженности признака, измеренного количественно.
применять
можно на малых выборках при n = 3 и более наблюдений.
Данный критерий предполагает ранжирование переменных на основе определённых правил.
Слайд 10Алгоритм нахождения U критерия:
Помечаем показатели первой выборки одним цветом,
а индивидуальные показатели второй выборки другим цветом.
Записываем данные в один
ряд по нарастанию признака независимо от того, к какой выборке они принадлежат.
Ранжируем значения. Всего рангов будет
Считаем сумму рангов, ориентируясь при этом на цвет показателей. Проверяем, совпадает ли она с расчётной суммой.
Считаем сумму рангов, ориентируясь при этом на цвет показателей. Проверяем, совпадает ли она с расчётной суммой.
Определяем большую ранговую сумму.
Определяем Uэмп по формуле:
где, n1 и n2 - число наблюдений, объёмы выборок;
- количество испытуемых с в группе с большей суммой рангов;
Тх – большая ранговая сумма.
Слайд 11Алгоритм нахождения U критерия:
Определяем критические значения по таблице, если Uэмп
< Uкр для р < 0,05, то различия достоверны/
Примечание: в
случаях, если объём выборок не совпадает, то необходимо рассчитать Uэмп и для меньшей ранговой суммы;
критерий U – Манна – Уитни является обратным, и поэтому чем меньше значение Uэмп, тем достовернее различия!
Слайд 12 Проведено исследование вербального интеллекта в подгруппе студентов первого
курса (n=10) и второго курса (n=11). Необходимо установить, различаются ли
группы между собой по выраженности рассматриваемого признака.
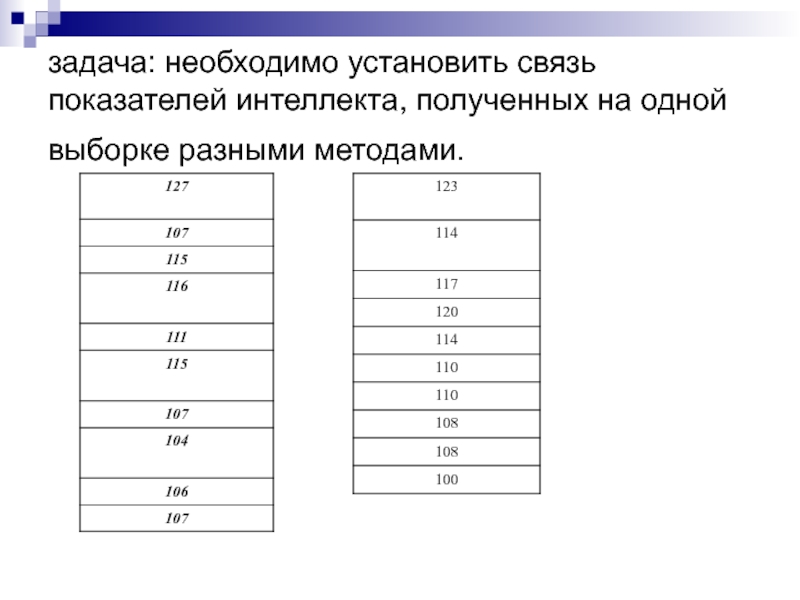
Слайд 13задача: необходимо установить связь показателей интеллекта, полученных на одной выборке
разными методами.