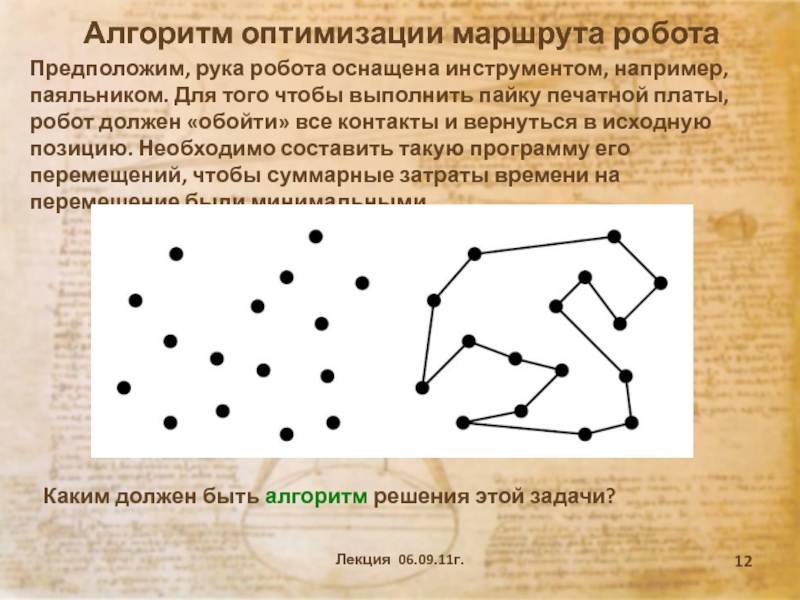
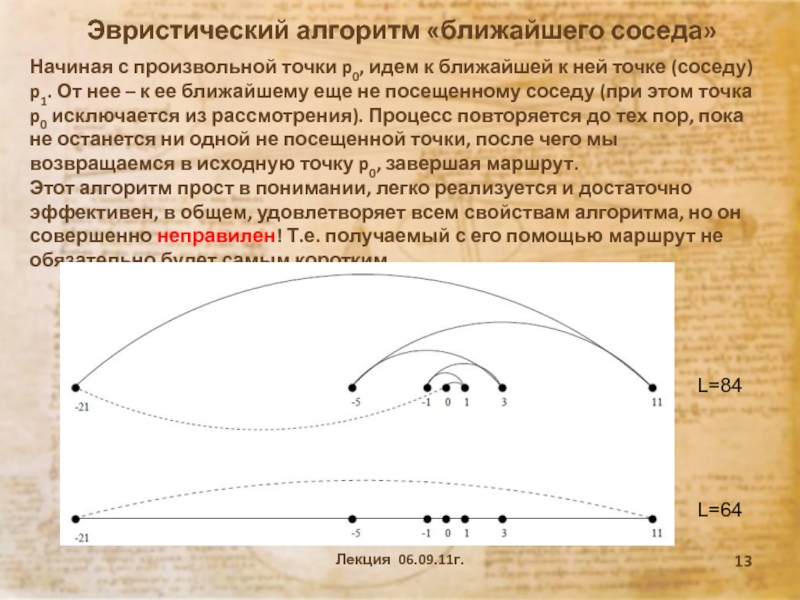
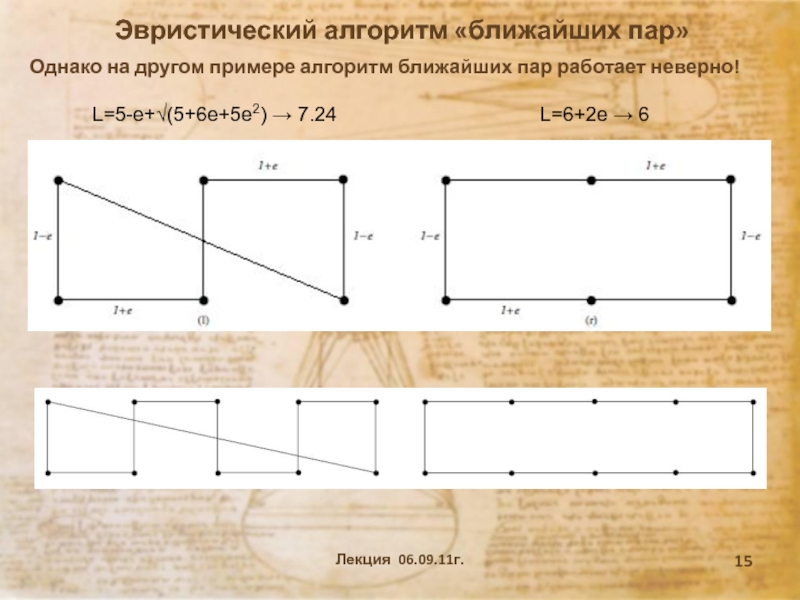
и терминов программирования как науки.
В результате изучения дисциплины студент должен:
Знать:
конструкции языка программирования высокого уровня, основные структуры данных, алгоритмы сортировки и поиска данных, базовые концепции парадигмы объектно-ориентированного программирования.Уметь: разрабатывать программы на языке высокого уровня, применяя изученные алгоритмы и структуры данных в соответствии с технологией разработки программ.
Демонстрировать способность и готовность к самостоятельному освоению новых алгоритмов, структур данных и парадигм программирования.
Лекция 06.09.11г.






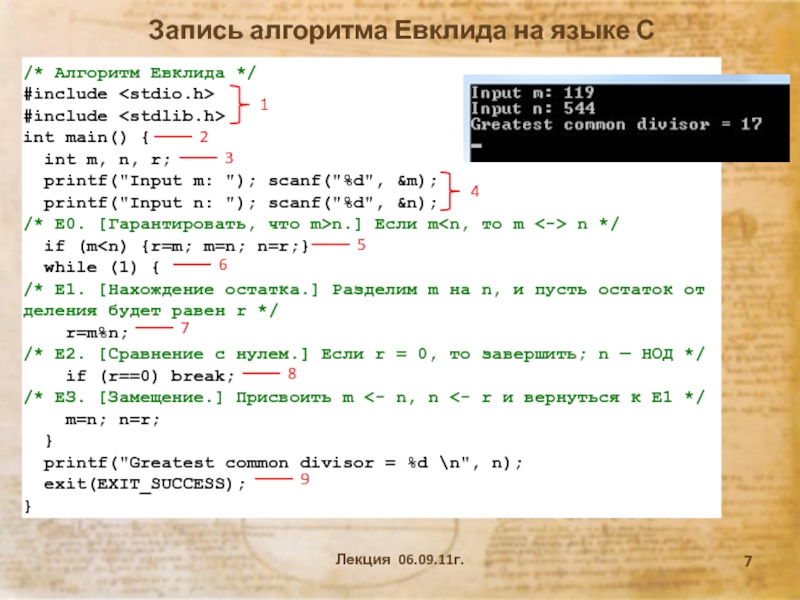
![Введение в дисциплину Основы алгоритмизации и программирования
Лекция Лекция 06.09.11г.Дональд Кнут – автор Библии программистовDonald Ervin Knuth (Дональд Кнут) Лекция 06.09.11г.Дональд Кнут – автор Библии программистовDonald Ervin Knuth (Дональд Кнут) [10.01.1938, Milwaukee, Wisconsin]автор так называемой Библии](/img/thumbs/554e894a6dc46359e8a78a016f424201-800x.jpg)