ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Содержание

1. ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА
2. 1.1. Волновые процессы. Продольные и поперечные волны.Упругими
3. ВОЛНЫПРОДОЛЬНЫЕПОПЕРЕЧНЫЕВ продольных волнах частицы среды колеблются в
4. Геометрическое место точек, до которых доходит возмущение
5. Геометрическое место точек, колеблющихся в одинаковой фазе,
6. Волна, фронт которой имеет вид плоскости, называется
7. 1.2. Уравнение бегущей волны. Фазовая скорость.Бегущими волнами
8. Уравнением волны называется выражение, которое дает смещение
9. (1.1)υ - скорость распространения волны (1.2)(1.2) - уравнение плоской волны, распространяющейся вдоль направления Х. (1.2`)
10. ϕ0 – начальная фаза волны, определяемая в
11. (1.4)(1.5)Волна, выраженная одним из уравнений (1.2) –
12. Если фазовая скорость в среде зависит от
13. Все точки среды колеблются по гармоническому закону
14. ϕ2– ϕ 1 = Δ ϕ =
15. 3) Энергия в случае бегущей волны переноситься
16. 1.3. Волновое уравнение.S – физическая величина, которая характеризует возмущение, распространяющееся в среде со скоростью υоператор Лапласа(1.11)
17. 1.4. Монохроматические и квазимонохроматические волны. Волновые группы.квазимонохроматическая волна(1.12)
18. 1.5. Принцип суперпозиции. Групповая скорость Принцип
19. Сконструируем простейший волновой пакет из двух распространяющихся
20. За скорость распространения этой негармонической волны (волнового
21. Рассмотрим связь между групповой и фазовой скоростями (1.14)(1.15)
22. Скачать презентанцию

1.1. Волновые процессы. Продольные и поперечные волны.Упругими волнами называются механические возмущения, распространяющиеся в упругой среде. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т.е.

Главная
Разное
ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Слайды и текст этой презентации

Слайд 1Лекция № 1
1. ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Слайд 21.1. Волновые процессы. Продольные и поперечные волны.
Упругими волнами называются механические

возмущения, распространяющиеся в упругой среде.
При изучении распространения колебаний не

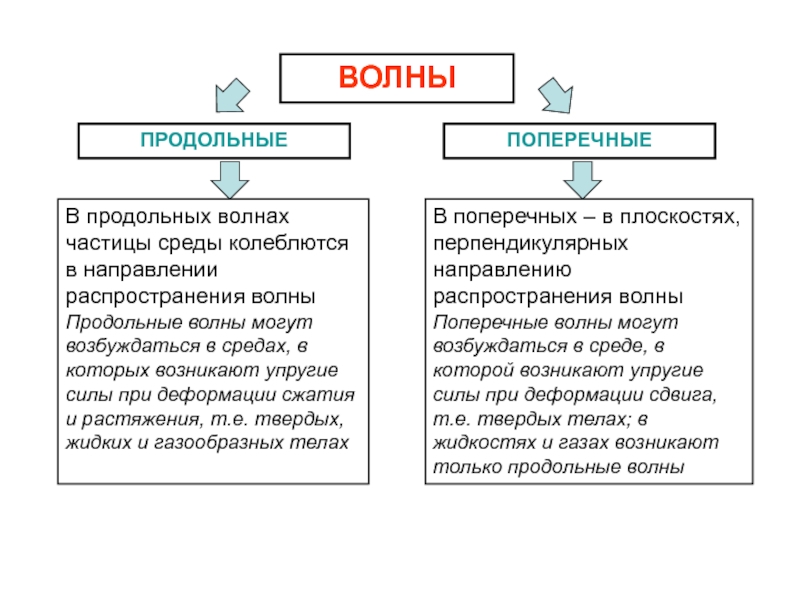
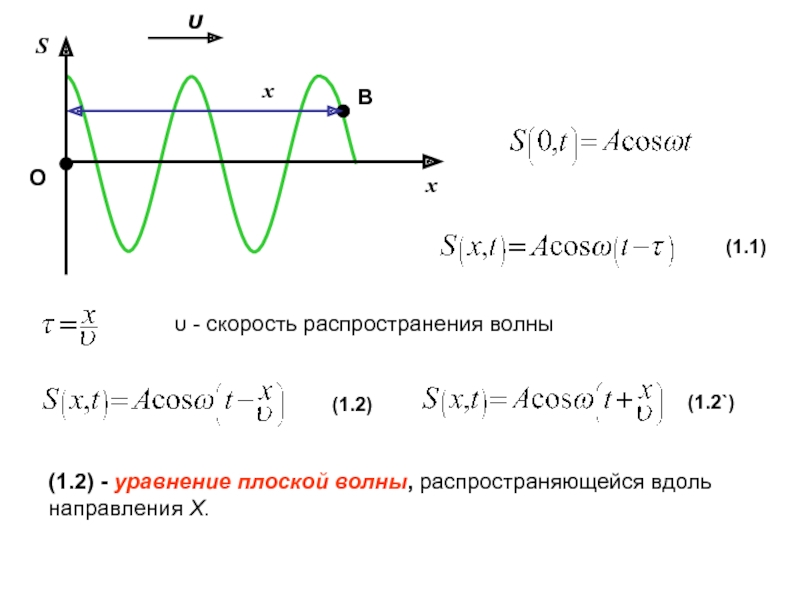
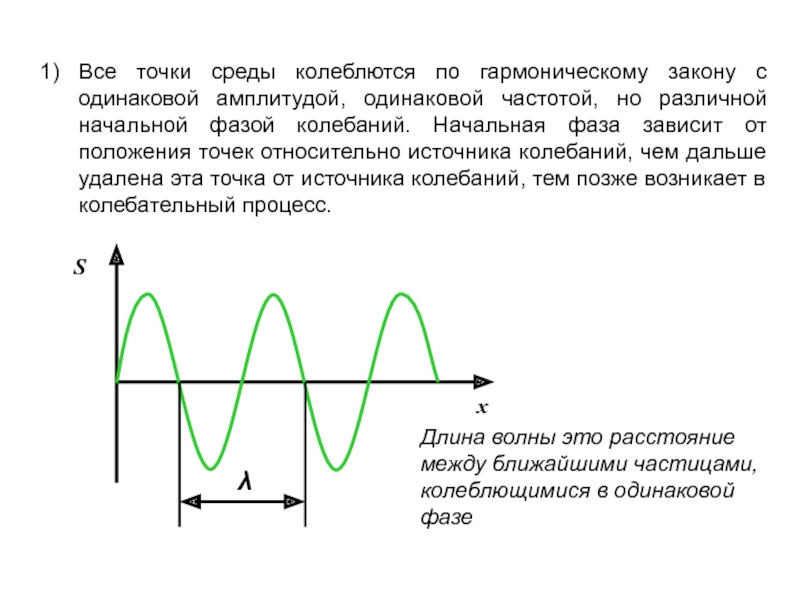
учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной).

Основным свойством всех волн является перенос энергии без переноса вещества.

1.1. Волновые процессы. Продольные и поперечные волны.Упругими волнами называются механические возмущения, распространяющиеся в упругой среде. При изучении

Слайд 3ВОЛНЫ
ПРОДОЛЬНЫЕ
ПОПЕРЕЧНЫЕ
В продольных волнах частицы среды колеблются в направлении распространения волны
Продольные

волны могут возбуждаться в средах, в которых возникают упругие силы

при деформации сжатия и растяжения, т.е. твердых, жидких и газообразных телах

В поперечных – в плоскостях, перпендикулярных направлению распространения волны
Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т.е. твердых телах; в жидкостях и газах возникают только продольные волны

ВОЛНЫПРОДОЛЬНЫЕПОПЕРЕЧНЫЕВ продольных волнах частицы среды колеблются в направлении распространения волныПродольные волны могут возбуждаться в средах, в которых

Слайд 4Геометрическое место точек, до которых доходит возмущение к моменту времени

t, называется фронтом волны (или волновым фронтом).
x
Волновой фронт
t

Геометрическое место точек, до которых доходит возмущение к моменту времени t, называется фронтом волны (или волновым фронтом).xВолновой

Слайд 5Геометрическое место точек, колеблющихся в одинаковой фазе, образует поверхность одинаковой

фазы, или волновую поверхность.
Волновая поверхность
Волновой фронт также является волновой поверхностью.

Геометрическое место точек, колеблющихся в одинаковой фазе, образует поверхность одинаковой фазы, или волновую поверхность.Волновая поверхностьВолновой фронт также

Слайд 6Волна, фронт которой имеет вид плоскости, называется плоской волной.

Если возмущение

исходит от точечного источника и распространяется во все стороны с

одинаковой скоростью, фронт волны имеет вид сферической поверхности с центром в источнике. Такая волна называется сферической.

Волна, фронт которой имеет вид плоскости, называется плоской волной.Если возмущение исходит от точечного источника и распространяется во

Слайд 71.2. Уравнение бегущей волны. Фазовая скорость.
Бегущими волнами называются волны, которые

переносят в пространстве энергию.
Перенос энергии волнами количественно характеризуется вектором

плотности потока энергии. Этот вектор для упругих волн называется вектором Умова.

Умов Н.А. (1846-1915) – русский ученый, решивший задачу о распространении энергии в среде

1.2. Уравнение бегущей волны. Фазовая скорость.Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами

Слайд 8
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как

функцию ее координат x, y, z в равновесном положении и

времени t:

S = f(x, y, z, t)

График зависимости S(х,t) в определенный момент времени называется формой возмущения.

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат x, y, z в

Слайд 9

(1.1)

υ - скорость распространения волны

(1.2)
(1.2) - уравнение плоской волны,

распространяющейся вдоль направления Х.
(1.2`)

Слайд 10

ϕ0 – начальная фаза волны, определяемая в общем случае выбором

начала отсчета x и t

– фаза плоской волны

Длина волны :

это расстояние между ближайшими частицами, колеблющимися в одинаковой фазе;
равна тому расстоянию, на которое распространяется определенная фаза колебаний за период.

(1.3)

ϕ0 – начальная фаза волны, определяемая в общем случае выбором начала отсчета x и t– фаза плоской

Слайд 11

(1.4)
(1.5)
Волна, выраженная одним из уравнений (1.2) – (1.5), называется монохроматической

волной

(1.6)

(1.7)
Для характеристики волн используется волновое число k
Найдем скорость распространения

монохроматической волны

Скорость υ распространения монохроматической волны – скорость перемещения фазы волны, и ее называют фазовой скоростью.

(1.4)(1.5)Волна, выраженная одним из уравнений (1.2) – (1.5), называется монохроматической волной (1.6)(1.7)Для характеристики волн используется волновое число

Слайд 12

Если фазовая скорость в среде зависит от их частоты, то

это явление называют дисперсией волн, а среда, в которой наблюдается

дисперсия волн, называется диспергирующей средой.

(1.5)

(1.8)

(1.7) совпадает с (1.8)

(1.10) – уравнение сферической волны

(1.10)

(1.9)

Если фазовая скорость в среде зависит от их частоты, то это явление называют дисперсией волн, а среда,

Слайд 13Все точки среды колеблются по гармоническому закону с одинаковой амплитудой,

одинаковой частотой, но различной начальной фазой колебаний. Начальная фаза зависит

от положения точек относительно источника колебаний, чем дальше удалена эта точка от источника колебаний, тем позже возникает в колебательный процесс.

Длина волны это расстояние между ближайшими частицами, колеблющимися в одинаковой фазе

Все точки среды колеблются по гармоническому закону с одинаковой амплитудой, одинаковой частотой, но различной начальной фазой колебаний.

Слайд 14

ϕ2– ϕ 1 = Δ ϕ = δ – разность

фаз.

х2 – х1 = Δ – разность хода.
Если Δ

= λ, то δ = 2π

Что и требовалось доказать.

ϕ2– ϕ 1 = Δ ϕ = δ – разность фаз. х2 – х1 = Δ –

Слайд 153) Энергия в случае бегущей волны переноситься в направлении распространения

волны.
2) В заданный момент времени колебания всех точек волны подчиняется

гармоническому закону. Каждая последующая точка стремиться занять место предыдущей.

3) Энергия в случае бегущей волны переноситься в направлении распространения волны.2) В заданный момент времени колебания всех

Слайд 16
1.3. Волновое уравнение.

S – физическая величина, которая характеризует возмущение, распространяющееся

в среде со скоростью υ

оператор Лапласа

(1.11)

1.3. Волновое уравнение.S – физическая величина, которая характеризует возмущение, распространяющееся в среде со скоростью υоператор Лапласа(1.11)

Слайд 171.4. Монохроматические и квазимонохроматические волны. Волновые группы.
квазимонохроматическая волна
(1.12)

Слайд 18
1.5. Принцип суперпозиции. Групповая скорость
Принцип суперпозиции (наложения) волн: при

распространении в линейной среде нескольких волн каждая из них распространяется

так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из следующих волновых процессов.

Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

1.5. Принцип суперпозиции. Групповая скорость Принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких

Слайд 19Сконструируем простейший волновой пакет из двух распространяющихся вдоль положительного направления

оси Х гармонических волн с одинаковыми амплитудами, близкими

частотами и волновыми числами, причем dω << ω, dk << k.

Сконструируем простейший волновой пакет из двух распространяющихся вдоль положительного направления оси Х гармонических волн с

Слайд 20За скорость распространения этой негармонической волны (волнового пакета) принимают скорость

перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве

центра волнового пакета.

(1.13)

Скорость u - групповая скорость

Групповая скорость - скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет

За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым

Слайд 21
Рассмотрим связь между групповой и фазовой скоростями

(1.14)

(1.15)

Скачать презентацию

Разделы презентаций

ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Содержание

Слайды и текст этой презентации

Слайд 1Лекция № 11. ВВЕДЕНИЕ В ВОЛНОВУЮ ТЕОРИЮ СВЕТА

Слайд 21.1. Волновые процессы. Продольные и поперечные волны.Упругими волнами называются механические

возмущения, распространяющиеся в упругой среде. При изучении распространения колебаний не

Слайд 3ВОЛНЫПРОДОЛЬНЫЕПОПЕРЕЧНЫЕВ продольных волнах частицы среды колеблются в направлении распространения волныПродольные

волны могут возбуждаться в средах, в которых возникают упругие силы

Слайд 4Геометрическое место точек, до которых доходит возмущение к моменту времени

t, называется фронтом волны (или волновым фронтом).xВолновой фронтt

Слайд 5Геометрическое место точек, колеблющихся в одинаковой фазе, образует поверхность одинаковой

фазы, или волновую поверхность.Волновая поверхностьВолновой фронт также является волновой поверхностью.

Слайд 6Волна, фронт которой имеет вид плоскости, называется плоской волной.Если возмущение

исходит от точечного источника и распространяется во все стороны с

Слайд 71.2. Уравнение бегущей волны. Фазовая скорость.Бегущими волнами называются волны, которые

переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором

Слайд 8Уравнением волны называется выражение, которое дает смещение колеблющейся точки как

функцию ее координат x, y, z в равновесном положении и

Слайд 9(1.1)υ - скорость распространения волны (1.2)(1.2) - уравнение плоской волны,

распространяющейся вдоль направления Х. (1.2`)

Слайд 10ϕ0 – начальная фаза волны, определяемая в общем случае выбором

начала отсчета x и t– фаза плоской волныДлина волны :

Слайд 11(1.4)(1.5)Волна, выраженная одним из уравнений (1.2) – (1.5), называется монохроматической

волной (1.6)(1.7)Для характеристики волн используется волновое число kНайдем скорость распространения

Слайд 12Если фазовая скорость в среде зависит от их частоты, то