Учебник Ю.Н. Макарычев и др. Учитель математики Омаров М.А.
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление значений функции по формуле
Содержание
- 1. Вычисление значений функции по формуле
- 2. Вычисление значений функции по формуле.Цель: знакомство с
- 3. а) Приведите примеры функций, укажите независимую и
- 4. Изучение нового материалаСпособ задания функции с помощью
- 5. Пример 1Рассмотрим функцию y(x)= x^2 + x.
- 6. Пример 2Рассмотрим функцию у(х) =1, если х
- 7. Пример 4Функция задана формулой у = 5х
- 8. При задании функции ее область определения иногда
- 9. Задание на урокеВыполнить упражнения: № 261; 265;
- 10. Слайд 10
- 11. Скачать презентанцию
Вычисление значений функции по формуле.Цель: знакомство с аналитическим способом задания функции.Ход урокаСообщение темы и цели урокаПовторение и закрепление пройденного материала
Слайды и текст этой презентации
Слайд 2Вычисление значений функции по формуле.
Цель: знакомство с аналитическим способом задания
функции.
Ход урока
Сообщение темы и цели урока
Повторение и закрепление пройденного материала
Слайд 3а) Приведите примеры функций, укажите независимую и зависимую переменные.
Пример.
S = 80*t где s-зависимая переменная , t-независимая переменная (или
аргумент).б) что называется областью определения и областью значения функции?
Ответы. Все значения которые может принимать независимая переменная (аргумент) называют областью определения .
Вес значения ,которые при этом принимает зависимая переменная (значения функции), образуют область значений функции.
Слайд 4Изучение нового материала
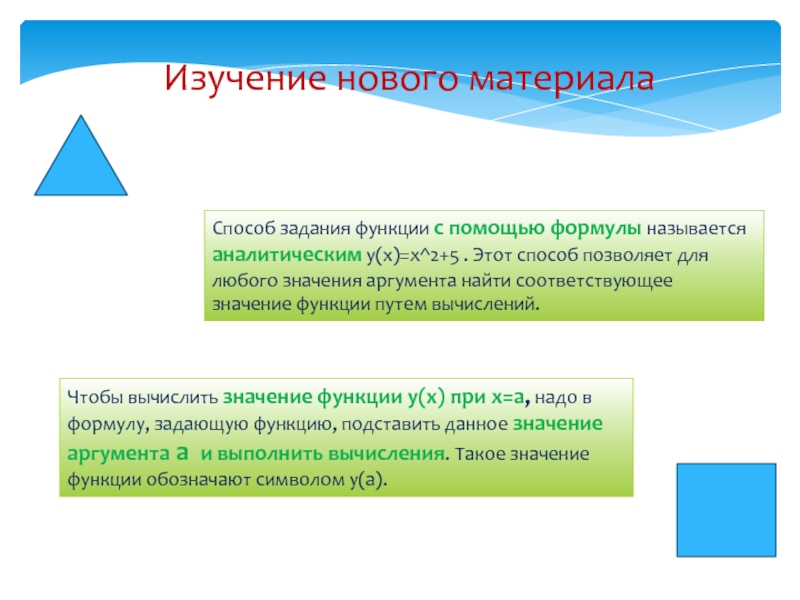
Способ задания функции с помощью формулы называется аналитическим
y(x)=x^2+5 . Этот способ позволяет для любого значения аргумента найти
соответствующее значение функции путем вычислений.Чтобы вычислить значение функции y(x) при x=a, надо в формулу, задающую функцию, подставить данное значение аргумента a и выполнить вычисления. Такое значение функции обозначают символом y(a).
Слайд 5Пример 1
Рассмотрим функцию y(x)= x^2 + x.
Это формула означает,
что для вычисления величины y необходимо возвести в квадрат значения
х и полученную величину сложить с самой величиной х.Поэтому, если х= -2, то у(-2) = (-2)^2 + (-2) = 4-2 = 2;
х= 4, то у(4) = 4^2 + 4 = 16 + 4 = 20;
х= а, то у(а) = а^2 + а;
х= 3а, то у(3а) = (3а)^2 + 3a =9а^2 +3а;
Слайд 6Пример 2
Рассмотрим функцию у(х) =
1, если х положительно;
0, если х
= 0;
-1, если х отрицательно.
Несмотря на некоторую непривычность, это выражение
также задает функцию и для любого значения х легко найти величину у.Если х = 4, то у(4) = 1 ( так как значение х = положительно, то пользуемся первой строчкой),
если х = 0, то у(0) = 0 ( пользуемся второй строчкой),
если х = -3,5 то у(-3,5) = -1 (пользуемся третьей строчкой).
Пример 3
Рассмотрим Функцию у(х) = |x|.
Если учесть определение модуля числа (выражения), то функцию можно записать в виде:
у(х) =
х, если х неотрицательно;
-х, если х отрицательно.
Для любого значения х можно найти у. Например, у(4,8) = 4,8 (так как х = 4,8 – число положительное, то пользуемся первой строчкой); у(0) = 0 ( так как х = 0 – число неотрицательное, то вновь используем первую строчку); у(-5) = -(-5) = 5 ( так как х= -5 – число отрицательное, пользуемся второй строчкой).
Слайд 7Пример 4
Функция задана формулой у = 5х – 7. Найдем,
при каком значении аргумента х значение функции у = 23.
Так
как у = 23, то подставив это значение в формулу у = 5х – 7. Получаем линейное уравнение 23 = 5х – 75х = 23 + 7
5х = 30
х = 6
Итак , при х = 6 значение у = 23
Заметим, что для нахождения значения аргумента х по известному значению функции у = b, надо подставить эту величину b вместо у в формулу функции. Получается уравнение с неизвестной х, корни которого и являются значениями аргумента.
Слайд 8При задании функции ее область определения иногда указывается.
Если она не
указана, то область определения состоит из всех значений аргумента, при
которых формула для функции имеет смысл.Пример 5
а) функция у =
5
(х-1)(х+3)
___________ , где 2< x < x 9. В этом примере область
определения указана – все значения х из промежутка 2< x < 9.
б) функция у =
__________. В этом случае область определения не указана.
4
(х–2)(х +6)
Найдем значение х, при котором формула для функции имеет смысл. Так как эта формула представляет собой дробь, то ее знаменатель (х-2)(х+6) не может равняться нулю, откуда х не равно 2 и -6. Итак, область определения данной функции – все значения х, кроме чисел -6 и 2.
Слайд 9Задание на уроке
Выполнить упражнения: № 261; 265; 266(а,в); 267; 271.
Задание
на дом
Выполнить упражнения: № 262; 266(б, г); 268; 272.
Подведение итогов урока
Теги
