Взаимно обратные функции D ( f ) E ( f ) y = f ( x ) x y 0 х Если каждому

Содержание

1. Взаимно обратные функции D ( f ) E ( f ) y = f ( x ) x y 0 х Если каждому
2. Задача. у = f (x), x
3. Дано:Найти: t – ?Решение:, т.е.Обратимая функцияОбратная функция к v( t )
4. Если функция у = f ( х
5. Дано:Найти функцию, обратную данной у = f -1(x).Решение: Ответ:
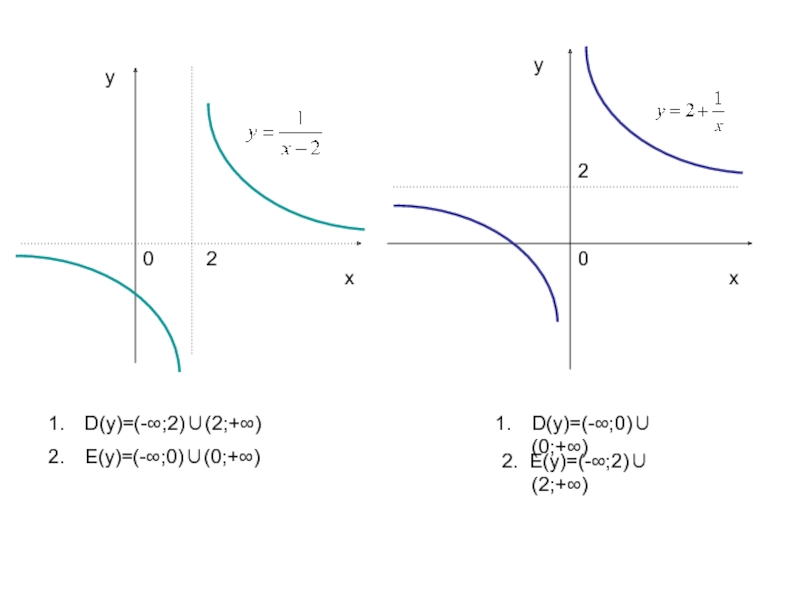
6. ххуу0022D(у)=(-∞;2)∪(2;+∞)Е(у)=(-∞;0)∪(0;+∞)2. Е(у)=(-∞;2)∪(2;+∞)D(у)=(-∞;0)∪(0;+∞)
7. Свойства обратных функций.Область определения обратной функции f
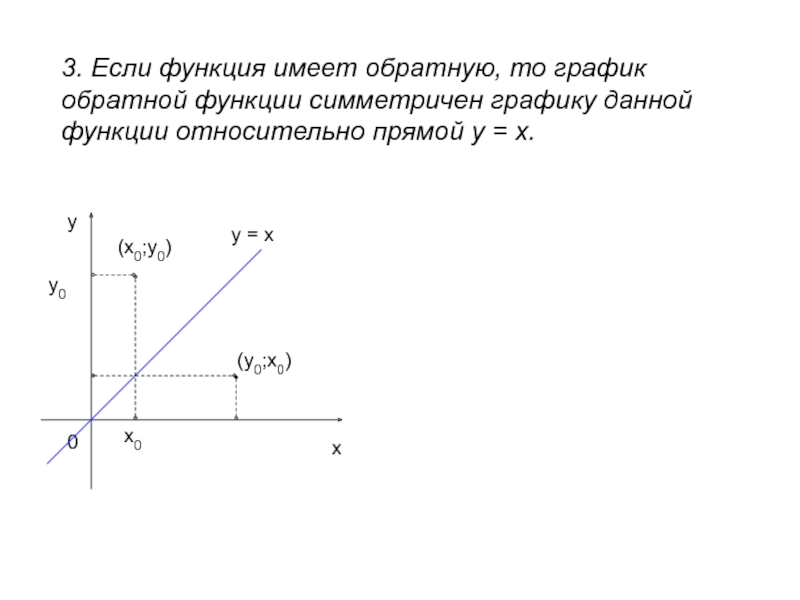
8. 3. Если функция имеет обратную, то график
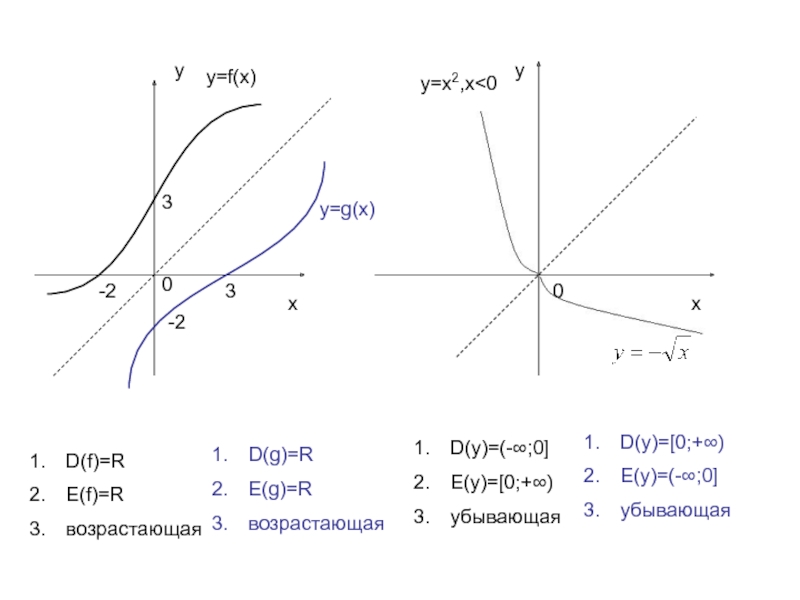
9. ухху0033-2-2у=f(x)у=g(x)y=x2,х
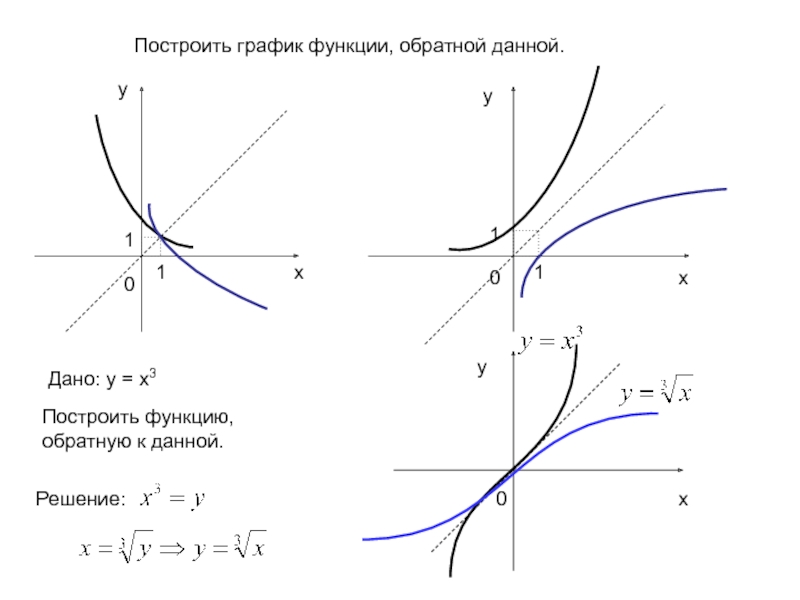
10. 111100хуухДано: у = х3Построить функцию, обратную к
11. Скачать презентанцию

Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у.

Главная
Разное
Взаимно обратные функции D ( f ) E ( f ) y = f ( x ) x y 0 х Если каждому

Слайды и текст этой презентации

Слайд 1Взаимно обратные
функции
Если каждому значению х из некоторого множества действительных чисел

поставлено в соответствие по определённому правилу f число у, то,

говорят, что на этом множестве определена функция.

Взаимно обратныефункцииЕсли каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определённому правилу f

Слайд 2Задача.
у = f (x), x - !
Найти

значение у при заданном значении х.
Задача.

у =

f (x), у- !

Найти значение х при заданном значении у.

Дано: у = 2х + 3
Найти: у (5)
Решение:
у (5) = 2 · 5 + 3 = 13
Ответ: у (5) = 13

Дано: у = 2х + 3, у (х) = 42
Найти: х
Решение:
42 = 2х + 3
2х = 39
х = 19,5
Ответ: у (19,5) = 42

Прямая

Обратная

Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача.

Слайд 3Дано:
Найти: t – ?
Решение:

, т.е.
Обратимая функция
Обратная функция к v( t

Слайд 4Если функция у = f ( х ) принимает каждое

своё значение у только при одном значении х, то эту

функцию называют обратимой.

Пусть у = f(x) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f(x) = y. Это соответствие определяет функцию х от у, которую обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).

Если функция у = f ( х ) принимает каждое своё значение у только при одном значении

Слайд 5Дано:
Найти функцию, обратную данной у = f -1(x).
Решение:
Ответ:

Слайд 6х
х
у
у
0
0
2
2
D(у)=(-∞;2)∪(2;+∞)
Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
D(у)=(-∞;0)∪(0;+∞)

Слайд 7Свойства обратных функций.
Область определения обратной функции f -1 совпадает с

множеством значений исходной f, а множество значений обратной функции f

-1 совпадает с областью определения исходной функции f: (запись f -1 означает – обратная функция ).
D(f -1) = E(f), E(f -1) = D(f).

Монотонная функция является обратимой:
если функция f возрастает, то обратная к ней функция f -1 также возрастает;
если функция f убывает, то обратная к ней функция f -1 также убывает.

Свойства обратных функций.Область определения обратной функции f -1 совпадает с множеством значений исходной f, а множество значений

Слайд 83. Если функция имеет обратную, то график обратной функции симметричен

графику данной функции относительно прямой у = х.
х
у
0
(х0;у0)
х0
у0
(у0;х0)
у = х

3. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у =

Слайд 9у
х
х
у
0
0
3
3
-2
-2
у=f(x)
у=g(x)
y=x2,х

Слайд 101
1
1
1
0
0
х
у
у
х
Дано: у = х3
Построить функцию, обратную к данной.
Решение:

х
у
0
Построить график функции, обратной данной.

111100хуухДано: у = х3Построить функцию, обратную к данной.Решение: ху0Построить график

Скачать презентацию

Разделы презентаций

Взаимно обратные функции D ( f ) E ( f ) y = f ( x ) x y 0 х Если каждому

Содержание

Слайды и текст этой презентации

Слайд 1Взаимно обратные
функции
Если каждому значению х из некоторого множества действительных чисел

поставлено в соответствие по определённому правилу f число у, то,

Слайд 2Задача.
у = f (x), x - !
Найти

значение у при заданном значении х.
Задача.

у =

Слайд 3Дано:
Найти: t – ?
Решение:

, т.е.
Обратимая функция
Обратная функция к v( t

Слайд 4Если функция у = f ( х ) принимает каждое

своё значение у только при одном значении х, то эту

Слайд 5Дано:
Найти функцию, обратную данной у = f -1(x).
Решение:
Ответ:

Слайд 6х
х
у
у
0
0
2
2
D(у)=(-∞;2)∪(2;+∞)
Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
D(у)=(-∞;0)∪(0;+∞)

Слайд 7Свойства обратных функций.
Область определения обратной функции f -1 совпадает с

множеством значений исходной f, а множество значений обратной функции f

Слайд 83. Если функция имеет обратную, то график обратной функции симметричен

графику данной функции относительно прямой у = х.
х
у
0
(х0;у0)
х0
у0
(у0;х0)
у = х

Слайд 9у
х
х
у
0
0
3
3
-2
-2
у=f(x)
у=g(x)
y=x2,х

Слайд 101
1
1
1
0
0
х
у
у
х
Дано: у = х3
Построить функцию, обратную к данной.
Решение:

х
у
0
Построить график функции, обратной данной.

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Взаимно обратные функции D ( f ) E ( f ) y = f ( x ) x y 0 х Если каждому

Содержание

Слайды и текст этой презентации

Слайд 1Взаимно обратныефункцииЕсли каждому значению х из некоторого множества действительных чисел

поставлено в соответствие по определённому правилу f число у, то,

Слайд 2Задача. у = f (x), x - ! Найти

значение у при заданном значении х. Задача. у =

Слайд 3Дано:Найти: t – ?Решение:, т.е.Обратимая функцияОбратная функция к v( t

Слайд 4Если функция у = f ( х ) принимает каждое

своё значение у только при одном значении х, то эту

Слайд 5Дано:Найти функцию, обратную данной у = f -1(x).Решение: Ответ:

Слайд 6ххуу0022D(у)=(-∞;2)∪(2;+∞)Е(у)=(-∞;0)∪(0;+∞)2. Е(у)=(-∞;2)∪(2;+∞)D(у)=(-∞;0)∪(0;+∞)

Слайд 7Свойства обратных функций.Область определения обратной функции f -1 совпадает с

множеством значений исходной f, а множество значений обратной функции f

Слайд 83. Если функция имеет обратную, то график обратной функции симметричен

графику данной функции относительно прямой у = х.ху0(х0;у0)х0у0(у0;х0)у = х

Слайд 9ухху0033-2-2у=f(x)у=g(x)y=x2,х

Слайд 10111100хуухДано: у = х3Построить функцию, обратную к данной.Решение:

ху0Построить график функции, обратной данной.

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Взаимно обратные
функции
Если каждому значению х из некоторого множества действительных чисел

Слайд 2Задача.
у = f (x), x - !
Найти

значение у при заданном значении х.
Задача.

у =

Слайд 3Дано:
Найти: t – ?
Решение:

, т.е.
Обратимая функция
Обратная функция к v( t

Слайд 5Дано:
Найти функцию, обратную данной у = f -1(x).
Решение:
Ответ:

Слайд 6х
х
у
у
0
0
2
2
D(у)=(-∞;2)∪(2;+∞)
Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
D(у)=(-∞;0)∪(0;+∞)

Слайд 7Свойства обратных функций.
Область определения обратной функции f -1 совпадает с

графику данной функции относительно прямой у = х.
х
у
0
(х0;у0)
х0
у0
(у0;х0)
у = х

Слайд 9у
х
х
у
0
0
3
3
-2
-2
у=f(x)
у=g(x)
y=x2,х

Слайд 101
1
1
1
0
0
х
у
у
х
Дано: у = х3
Построить функцию, обратную к данной.
Решение:

х
у
0
Построить график функции, обратной данной.