Взаимодействие в двухкомпонентных системах Примитивные виды взаимодействия: без

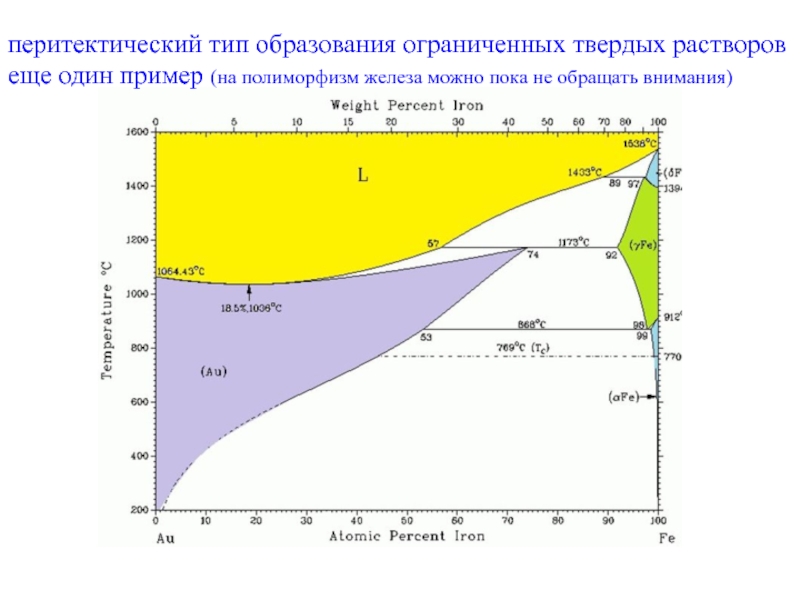
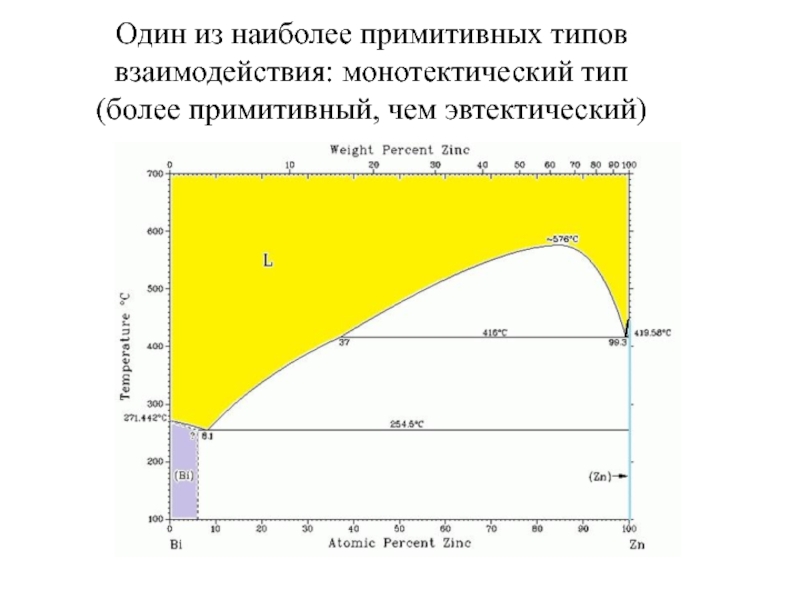
B. Должны быть переменные: P, T, xA, xB
Но можно обойтись

набором трёх (а не четырех) переменных: P, T, xB, т.к. xB = 1 – xA
Должна быть трехмерная диаграмма с осями P, T, xB.
Зафиксируем первые две переменные: P = const, T=const.
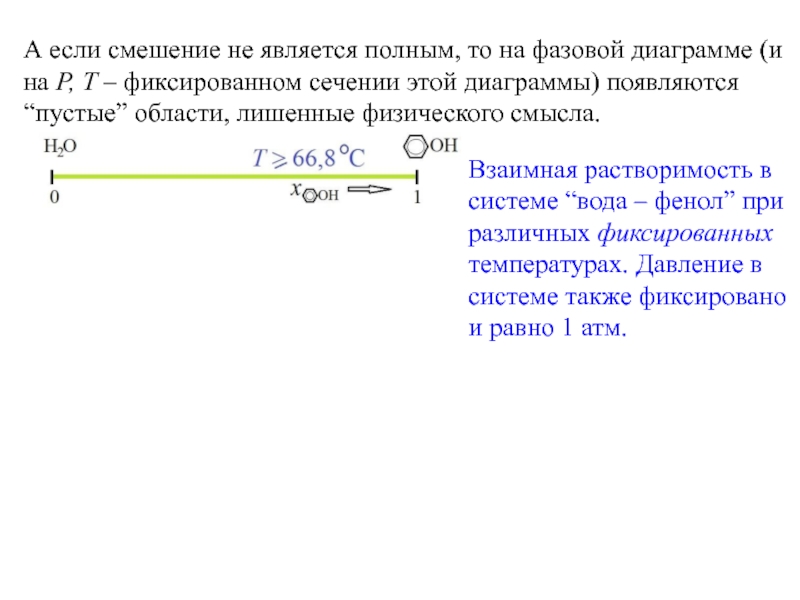
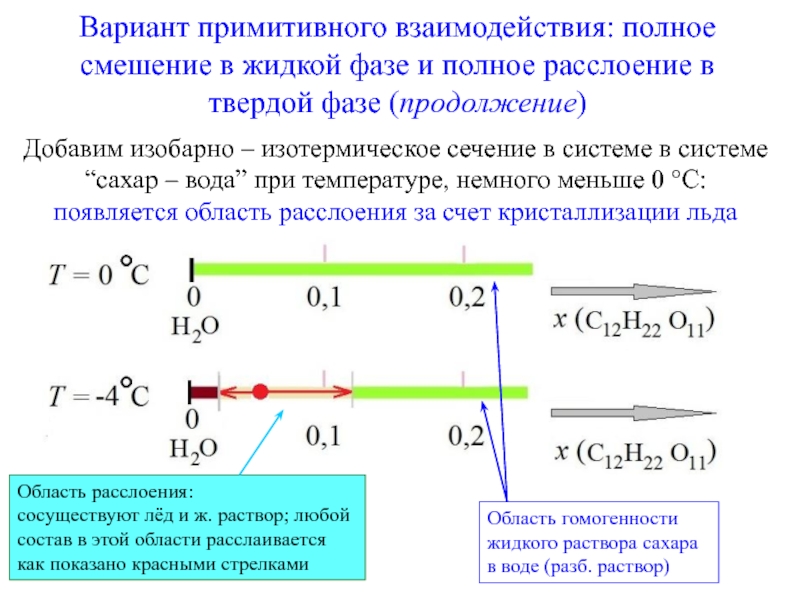
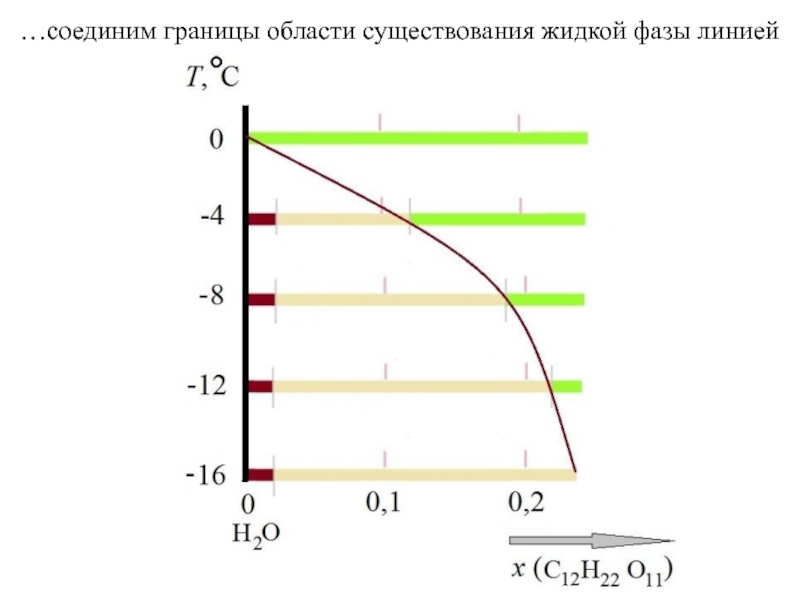
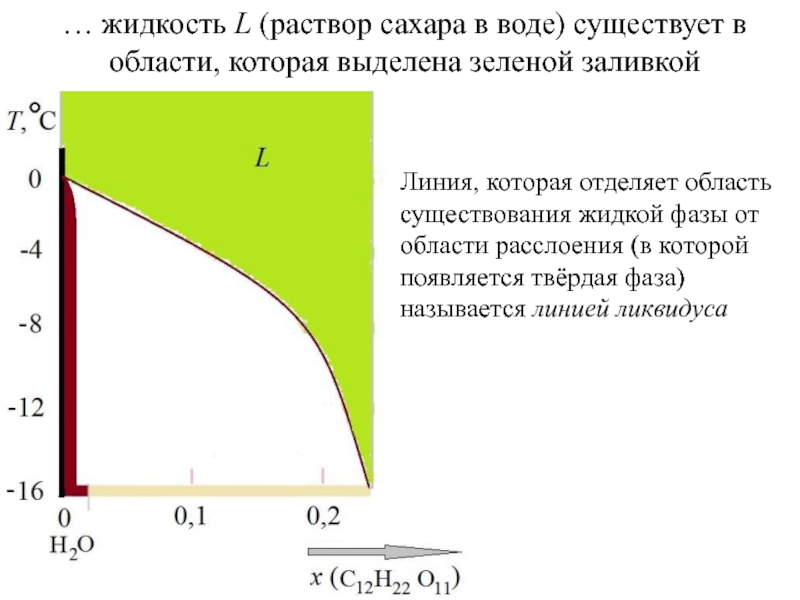
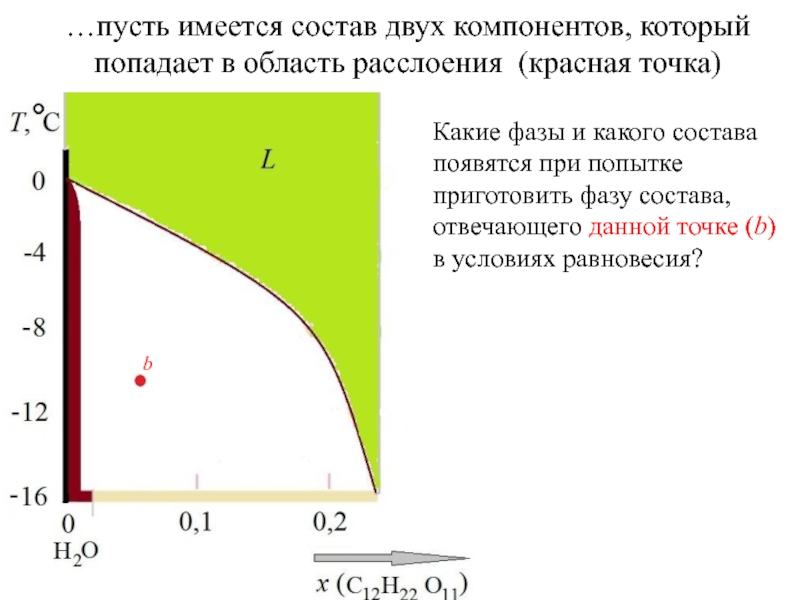
Пространство состояний в этом случае представлено числовым отрезком. Если происходит полное смешивание A и B при P = const, T=const, то весь этот числовой отрезок [0, 1] и представляет собой P, T – фиксированную области гомогенности. A B
0 xB→ 1

(и на P, T – фиксированном сечении этой диаграммы) появляются

“пустые” области, лишенные физического смысла.

Взаимная растворимость в системе “вода – фенол” при различных фиксированных температурах. Давление в системе также фиксировано и равно 1 атм.

температурах. Давление в системе также фиксировано и равно 1 атм
...

а теперь поместим все концентрационные отрезки на ось температур...

... и соединим границы областей гомогенности, полученные при разных температурах плавными линиями..

 Получаем T-x сечение бинарной диаграммы
“вода – фенол”
для P = 1 атм

температурах. Давление в системе также фиксировано и равно 1 атм
T-x

сечение системы “H2O-C6H5OH”

... а теперь пометим область существования (область гомогенности) жидкой фазы (осуществим заливку зеленым цветом).

Полузаконный приём: P можно жестко и не фиксировать. Не слишком большие (десятки атм) варьирования давления мало сказываются на состоянии конденсированных (ж. и тв.) фаз! Именно только такие фазы и рассматриваем далее. Тогда правило фаз можно условно записывать как
Ф + С = K +1
и говорить о T-x диаграмме системы.

P = 1 атм

(разб. раствор)
Построим изобарно – изотермическое сечение в системе “сахароза –

вода” при температуре 0С в области существования жидкого раствора (при низких концентрациях сахара).

полное смешение в жидкой фазе...

... и полное расслоение в твердых фазах

расслоение в твердой фазе (продолжение)
Область гомогенности
жидкого раствора сахара
в

воде (разб. раствор)

Добавим изобарно – изотермическое сечение в системе в системе “сахар – вода” при температуре, немного меньше 0 С: появляется область расслоения за счет кристаллизации льда

Область расслоения:
сосуществуют лёд и ж. раствор; любой состав в этой области расслаивается как показано красными стрелками

раствор становится всё более концентрированным

которая выделена зеленой заливкой
Линия, которая отделяет область существования жидкой

фазы от области расслоения (в которой появляется твёрдая фаза) называется линией ликвидуса

(красная точка)
Какие фазы и какого состава появятся при попытке приготовить

фазу состава, отвечающего данной точке (b) в условиях равновесия?

b

границы существования областей каждой из фаз в определенных точках (точки

a и c). Эти точки и будут отвечать составам сосуществующих фаз. Отношения количеств фаз определяется исходя из “правила рычага”:
(nS/nL) = (ab/bc)-1

охлаждении (например, охлаждаем раствор от условий, соотв. точке b)?
Уравнение

Шрёдера – Ле-Шателье:
ln(1-xB) = -(DHпл./RT 2пл.А)∙DT;
где DT = (Tпл.А - T)
Для неидеальных р-ров xB надо менять на aB
Для данного примера A=H2O, B=C12H22O11
Криоскопическое приближение:
xB = (DHпл./RT 2пл.А)∙DT 
DT = (RT 2пл.А/ DHпл. ) ∙ xB

же самое) отвечает на вопрос: “Какой температуре соответствует первичная кристаллизация

раствора”? Кристаллизуется растворитель!

для обеих ветвей ликвидуса

ln(1-xB) = -(DHпл.A/RT 2пл.А)∙(T пл.А - T)
ln(xB)

= -(DHпл.B/RT 2пл.B)∙(T пл.B - T)

с неизвестными T и xB (для реального раствора – с переменными T и aB)

P.S. Еще некоторые важные моменты – применение правила фаз, построение кривых нагревания/охлаждения и некоторые др. – см. конспекты лекций (разбирается на доске с мелом).

типа) такой объект – ФД с ретроградным солидусом...

гомогенности тв. р-ра на основе Zn)
! На линии ликвидуса (со

стороны ретроградной растворимости) часто встречается перегиб, близкий по температуре максимальной растворимости примеси в твердой фазе

Кажущийся парадокс: для диаграмм такого типа возможны такие диапазоны температур и составов, в которых увеличение температуры приводит к кристаллизации, а уменьшение T – к плавлению (см. следующий слайд – область, выделенную стрелками ).


типа

Примеры этой и других гетероструктур эвтектических сплавов см. на рис.

справа.

Микроструктура эвтектик. По работе Тарана и Мазура, 1978.

а - Sb+Zn4Sb3, ув.х200; б - Sb + Cu2Sb, ув. х 400; в - Fe+Fe3C, ув. х 400; г - Fe+C, ув. х 150; д - Fe+W6C, ув.х 250; е - Fe+MoC, ув. х 500; ж - Zn+MgZn2, ув. х1000; з - Al+FeAlSi, ув. х 500; и- Pb + Sb, ув. x 200.

железа можно пока не обращать внимания)

эвтектический)