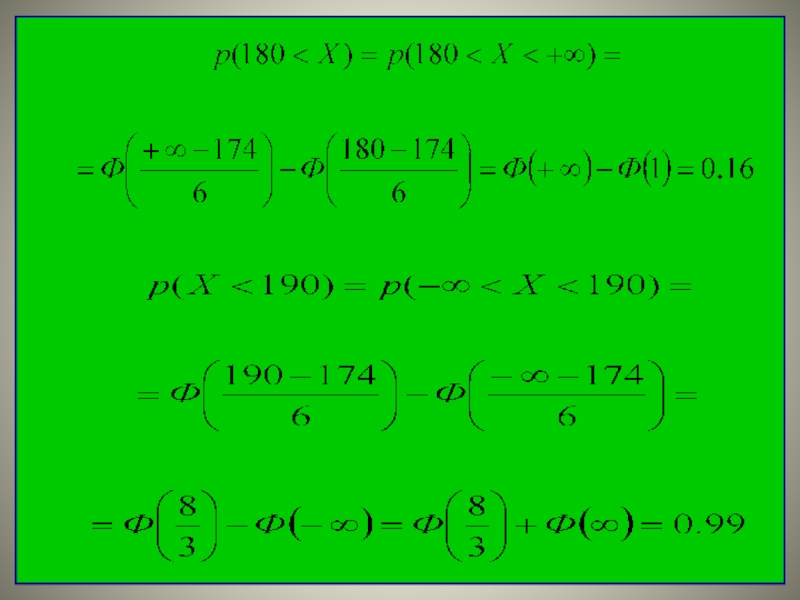Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Равномерное распределение случайных величин
Содержание
- 1. Равномерное распределение случайных величин
- 2. Учебный вопрос №1Равномерное распределение НСВ
- 3. Рассмотрим непрерывную случайную величину Х, возможные значения
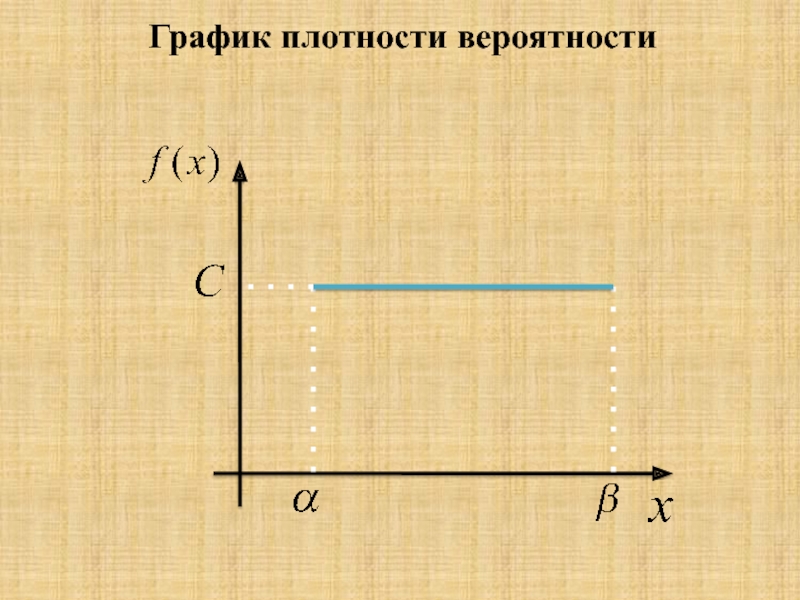
- 4. График плотности вероятности
- 5. Выразим параметр С через α и β.
- 6. Плотность вероятности равномерно распределенной случайной величины
- 7. Найдем функцию распределения:
- 8. Функция распределения равномерно распределенной случайной величины
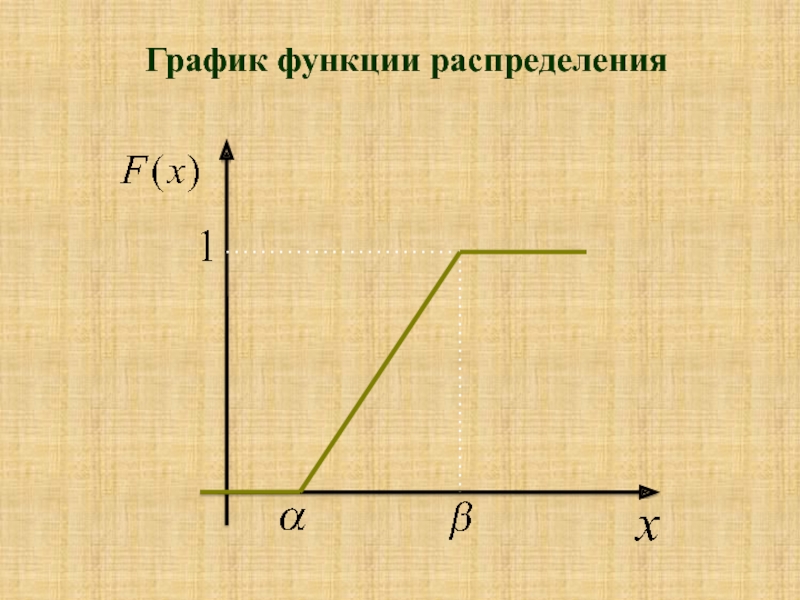
- 9. График функции распределения
- 10. Вычислим математическое ожидание и дисперсиюслучайной величины, подчиняющейся равномерному распределению.
- 11. Слайд 11
- 12. Тогда среднеквадратичное отклонение будет иметь вид:
- 13. Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0
- 14. Для нахождения искомых вероятностей используем формулу:Где F(α)
- 15. Слайд 15
- 16. Учебный вопрос №2Нормальное распределение НСВ
- 17. Нормальный (гауссов) закон распределенияНепрерывная случайная величина
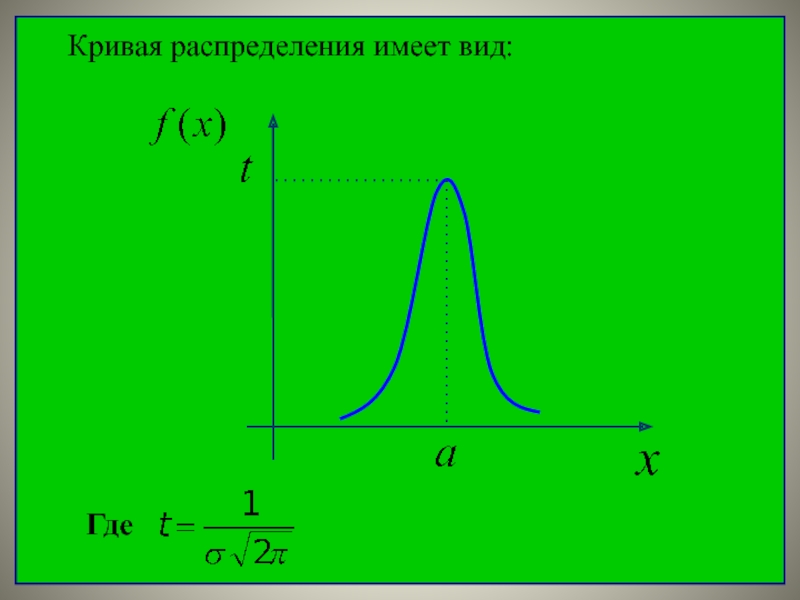
- 18. Кривая распределения имеет вид:Где
- 19. Выясним смысл параметров распределения Гаусса. Для этого
- 20. Разбиваем на сумму двух интегралов:Второй интеграл представляет собой интеграл Пуассона:
- 21. В первом интеграле вносим t под знак
- 22. Этот интеграл берем по частям:
- 23. Первое слагаемое в скобках равно 0, так
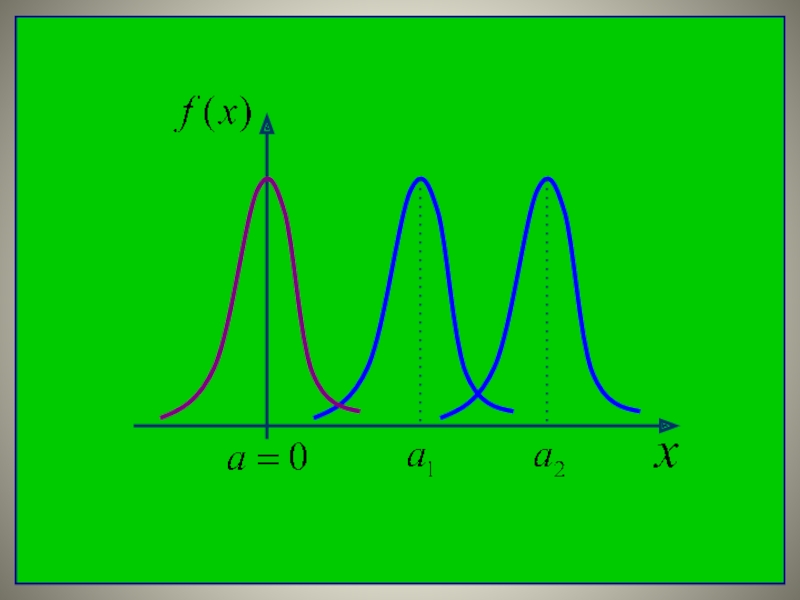
- 24. Если изменять параметр a , кривая распределения
- 25. Слайд 25
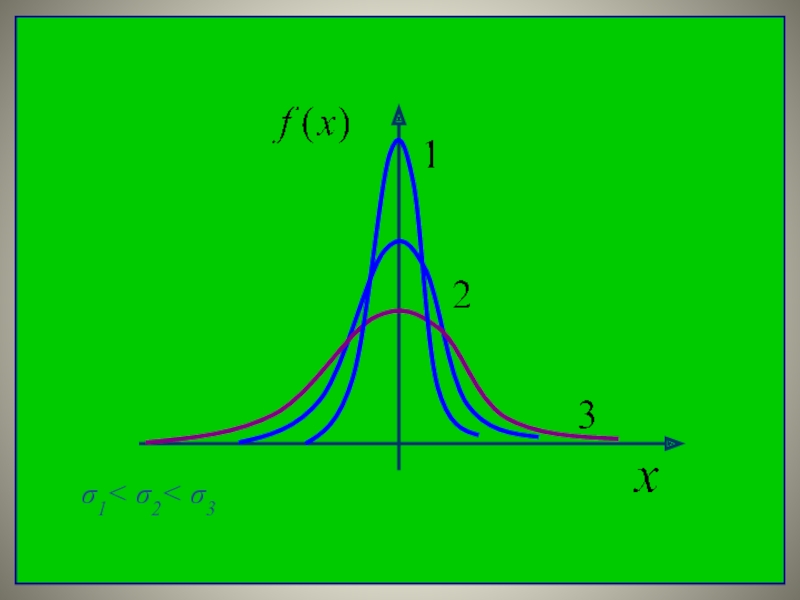
- 26. Параметр σ характеризует не положение, а саму
- 27. σ1< σ2< σ3
- 28. То, что случайная величина Х распределена по
- 29. Найдем функцию распределения случайной величины Х . Сделаем замену переменной:
- 30. Последний интеграл не выражается через элементарные функции,
- 31. Функция Ф*(х) называется нормальной функцией распределения.Ее значения
- 32. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СВ НА ЗАДАННЫЙ УЧАСТОК
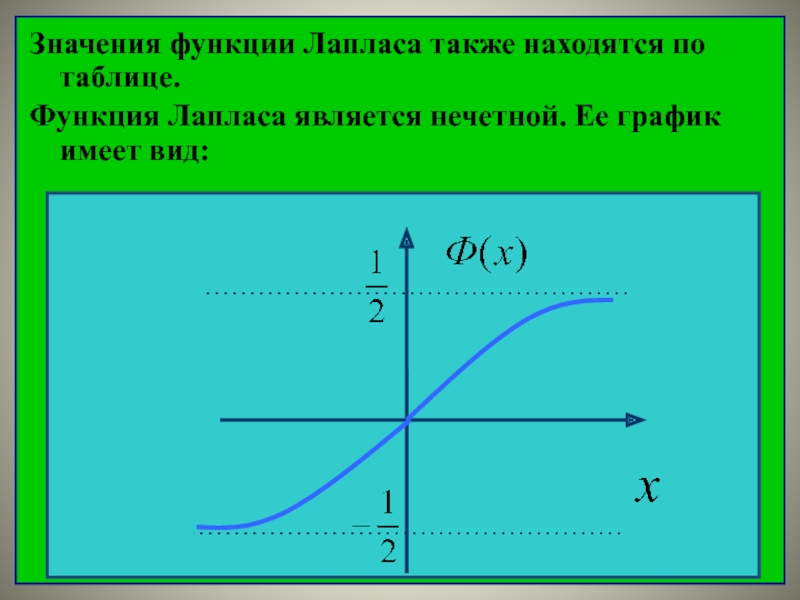
- 33. Значения функции Лапласа также находятся по таблице. Функция Лапласа является нечетной. Ее график имеет вид:
- 34. Пусть Х - нормально распределенная случайная величина с параметрами a, σ. ТогдаПРАВИЛО ТРЕХ СИГМ
- 35. Действительно,
- 36. Пусть случайная величина Х - рост наугад
- 37. Сначала определим параметр σ. Используем правило
- 38. Слайд 38
- 39. Слайд 39
- 40. Учебный вопрос №3Показателное распределение НСВ
- 41. Пусть непрерывная случайная величина Х задана функцией
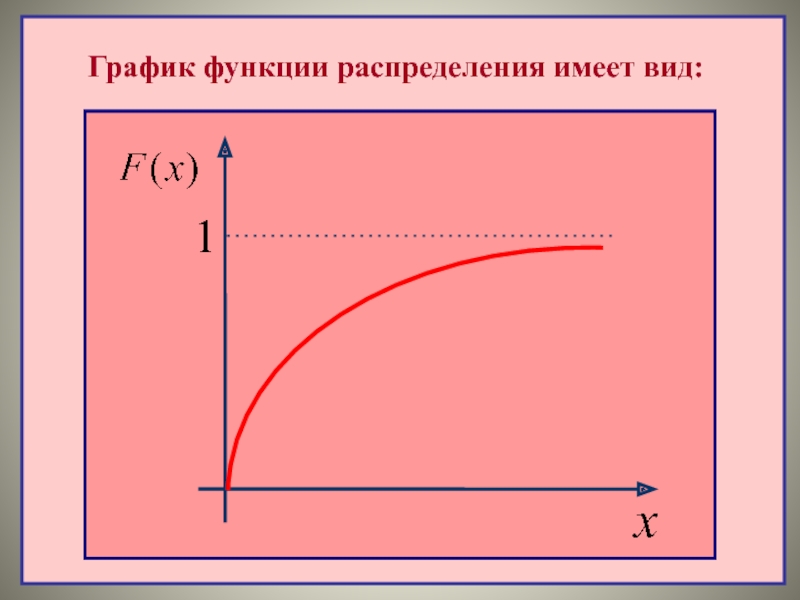
- 42. График функции распределения имеет вид:
- 43. Найдем плотность вероятности этой случайной величины.Плотность вероятности
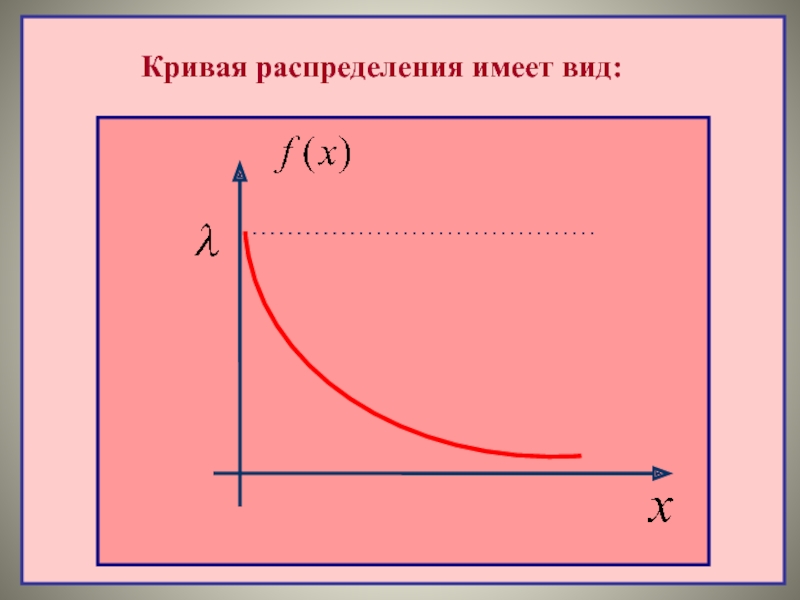
- 44. Кривая распределения имеет вид:
- 45. Найдем математическое ожидание и дисперсию случайной величины,
- 46. Полученный определенный интеграл будем брать по частям:
- 47. Первые два слагаемых в пределе равны 0,
- 48. Как и в предыдущем случае, переходим к пределу определенного интеграла:Берем интеграл по частям:
- 49. Полученный интеграл еще раз берем по частям:Полученный интеграл табличный:
- 50. Подставляем пределы интегрирования:Теперь находим дисперсию и среднеквадратичное отклонение:
- 51. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция
Тема: Некоторые законы распределения непрерывных случайных величин
Учебные вопросы:
Равномерное распределение НСВ.
Слайд 3Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в
некотором интервале и равновероятны.
Плотность вероятности такой случайной величины будет иметь
вид:Где с - некоторая постоянная.
Равномерное распределение
Слайд 5
Выразим параметр С через α и β. Для этого используем
тот факт, что интеграл от плотности вероятности по всей области
должен быть равен 1:
Слайд 10Вычислим математическое ожидание и дисперсию
случайной величины, подчиняющейся равномерному распределению.
Слайд 13Пусть случайная величина Х
равномерно распределена на
участке [0;100]. Найти
вероятности:
Р(0
Слайд 14Для нахождения искомых вероятностей используем формулу:
Где F(α) и F(β) -
функция распределения на концах рассматриваемого интервала. Для равномерного распределения
На
интервале от α доβ. Поэтому Решение примера
Слайд 17
Нормальный (гауссов)
закон распределения
Непрерывная случайная величина Х
называется распределенной
по
нормальному закону с параметрами
a, σ>0, если она имеет плотность
вероятности
Слайд 19
Выясним смысл параметров распределения Гаусса. Для этого вычислим характеристики этого
распределения (математическое ожидание и дисперсию).
Делаем замену переменной:
Слайд 21
В первом интеграле вносим t под знак дифференциала:
Таким образом, параметр
a представляет собой математическое ожидание случайной величины.
Теперь найдем дисперсию:
Делаем
замену переменной:Слайд 23
Первое слагаемое в скобках равно 0, так как экспонента в
минус бесконечной степени будет стремиться к нулю быстрее, чем возрастает
любая степень t.Этот интеграл представляет собой интеграл Пуассона:
Тогда параметр σ представляет собой среднеквадратичное отклонение.
Слайд 24
Если изменять параметр a ,
кривая распределения будет
смещаться вдоль
оси
абсцисс, не изменяя при этом
своей формы.
Слайд 26
Параметр σ характеризует
не положение, а саму форму
кривой распределения.
При его увеличении кривая
распределения становится более
плоской, и наоборот.
Слайд 28
То, что случайная величина Х распределена по нормальному закону с
параметрами a, σ>0 , обозначается
При вычислении вероятностей такая случайная
величина сводится к случайной величине
Слайд 30
Последний интеграл не выражается через элементарные функции, но его можно
вычислить через специальную функцию (так называемый интеграл вероятностей):
Эта функция представляет
собой функцию распределения нормальной случайной величины с параметрами a=0, σ=1. Слайд 31
Функция Ф*(х) называется нормальной функцией распределения.
Ее значения приведены в таблицах.
Но
большее распространение имеет функция Лапласа
Так как
То
Слайд 33
Значения функции Лапласа также находятся по таблице.
Функция Лапласа является
нечетной. Ее график имеет вид:
Слайд 34
Пусть Х - нормально распределенная
случайная величина с параметрами
a,
σ. Тогда
ПРАВИЛО ТРЕХ СИГМ
Слайд 36
Пусть случайная величина Х - рост
наугад выбранного студента
подчиняется
нормальному
распределению с параметром a=174 см.
Определить приближенно
параметр σ,
полагая, что практическивсе студенты имеют рост в
пределах от 156 до
192 см и найти вероятности р(Х>180),
p(X<190), p(160
ПРИМЕР
Слайд 37
Сначала определим параметр σ. Используем правило «3 сигм». Параметр
a=174 см определяет средний рост студентов.
Причем 174-3σ=156, 174+ 3σ=192.
Отсюда
σ=6.Таким образом,
РЕШЕНИЕ.








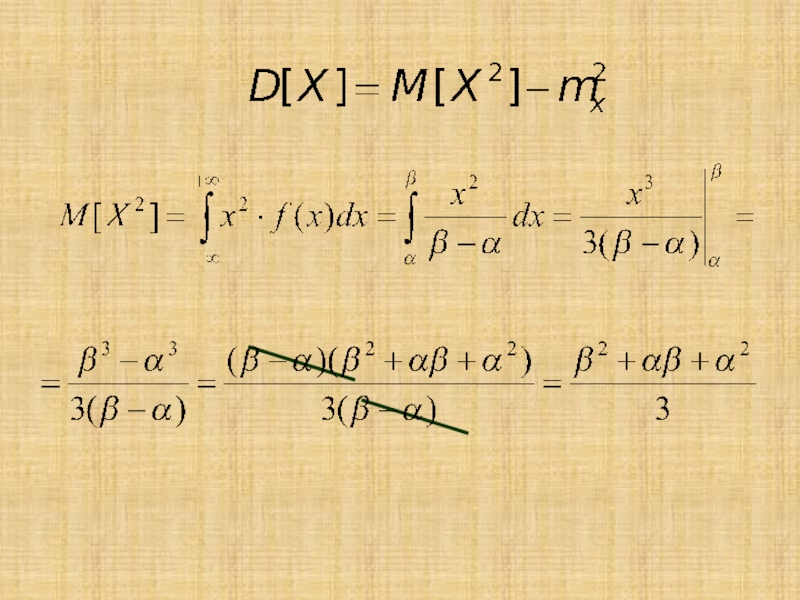

![Равномерное распределение случайных величин Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0 Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0](/img/thumbs/3fa6f7952e86ab02e7ddb869db7fb1c4-800x.jpg)