Слайд 1Задача хемометрики - разработка и применение методов извлечения информации о
веществе из результатов эксперимента.
При этом хемометрика имеет дело больше с
качественным аспектом, а метрология - с количественным.
Для всех методов аналитической химии можно выделить общие черты:
· получение информации
· обработка информации
· оценка достоверности
Слайд 5Аналитический процесс
1. Постановка задачи
2. Выбор метода и методики
3. Отбор пробы
4.
Пробоподготовка
5. Измерение аналитического сигнала
6. Обработка информации, оценка и интерпретация результатов
оперативный
контроль точности
- статистический контроль точности
Слайд 6Измерение - получение любых количественных характеристик материальных объектов опытным путем.
Измерения
бывают прямыми (когда объект непосредственно сопоставляется с носителем единицы измерения,
например, измерение длины линейкой) и косвенными (когда измеряемая величина рассчитывается из других измеренных величин, например, измерение глубины с помощью эхолота)
Необходимо обеспечить единство измерений, т.е. чтобы результат измерения не зависел от времени, места, человека и т.д.
Слайд 7Для этого нужны:
1. Единицы измерения (например, система СИ)
2. Эталоны
3. Средства
измерения (приборы и меры, которые делятся на рабочие и образцовые)
4.
Поверочная схема - документ, регламентирующий порядок взаимодействия рабочих и образцовых средств измерения различного уровня.
Причем эти пункты 1-4 легко реализуются только в случае прямых измерений
Химия имеет дело только с косвенными измерениями
Слайд 8В качестве мер использовать стандартные образцы или образцы сравнения.
Образец сравнения
- материал (обычно специально приготовленый), состав которого достаточно надежно известен.
Стандартный
образец - образец сравнения, состав которого официально (юридически) удостоверен.
Стандарные образцы не универсальны (не взаимозаменяемы) - существуют стандартные образцы почвы, сплавов и т.д. даже если речь идет об определении одного и того же элемента.
Образцы сравнения готовятся каждый раз заново.
Слайд 9Аналитический сигнал - физическая величина, доступная измерению (обычно прямому) и
функциональна связанная с содержанием вещества.
A = f(x), где A -
аналитический сигнал, f - градуировочная функция, x - содержание.
Таким образом, измерение распадается на получение градуировочной функции и собственно измерение.
Где взять градуировочную функцию? Методы анализа бывают абсолютными (например, гравиметрия, где градуировочная функция выводится из теоретических посылок) и относительными (где градуировочная функция устанавливается экспериментально)
Слайд 10Градуировка - процесс построения градуировочной функции опытным путем. Абсолютные методы
градуировки не требуют.
Пример: Неявно градуировка присутствует даже в таком методе,
как титриметрия. Концентрация титранта устанавливается через стандартизацию, а затем уже эта величина используется для вычисления концентрации в неизвестном образце.
Слайд 11Обычно градуировка строится следующим способом: берется ряд образцов сравнения, выполняются
все стадии методики, измеряется аналитический сигнал, затем строится функция.
При
этом необходимо особое внимание обратить на следующие пункты:
· надежность образца сравнения (насколько точно известен состав?)
· аналитический сигнал зависит не только от содержания, но и от условий эксперимента: физических, химических, связанных с режимом работы прибора...
· Условия градуировки и измерения должны быть максимально идентичны
· какова погрешность измерения (и самой градуировки)?
Слайд 12Метрологические категории
Метрологическая категория - характеристика одного качества результата измерений или
измерительной процедуры в целом.
Погрешность - любое отличие результата измерений от
истинного значения измеряемой величины.
Как основной постулат метрологии принимается утверждение:
Любой результат измерений всегда содержит погрешность.
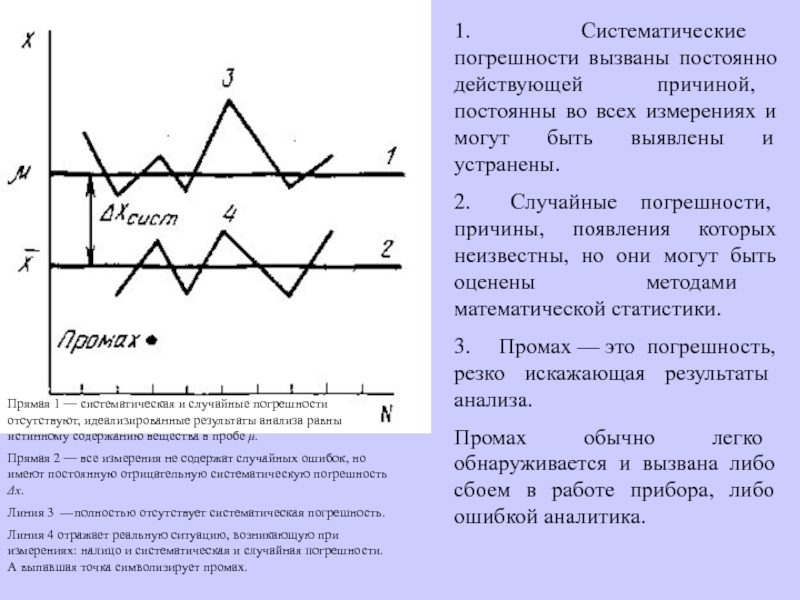
Слайд 131. Систематические погрешности вызваны постоянно действующей причиной, постоянны во всех
измерениях и могут быть выявлены и устранены.
2. Случайные погрешности, причины,
появления которых неизвестны, но они могут быть оценены методами математической статистики.
3. Промах — это погрешность, резко искажающая результаты анализа.
Промах обычно легко обнаруживается и вызвана либо сбоем в работе прибора, либо ошибкой аналитика.
Прямая 1 — систематическая и случайные погрешности отсутствуют, идеализированные результаты анализа равны истинному содержанию вещества в пробе .
Прямая 2 — все измерения не содержат случайных ошибок, но имеют постоянную отрицательную систематическую погрешность х.
Линия 3 полностью отсутствует систематическая погрешность.
Линия 4 отражает реальную ситуацию, возникающую при измерениях: налицо и систематическая и случайная погрешности. А выпавшая точка символизирует промах.
Слайд 14С систематическими и случайными погрешностями связаны понятия воспроизводимости и правильности.
Воспроизводимость характеризует степень близости друг к другу единичных определений, рассеяния
единичных определений относительно среднего. Правильность характеризует отклонение полученного результата анализа от истинного значения измеряемой величины
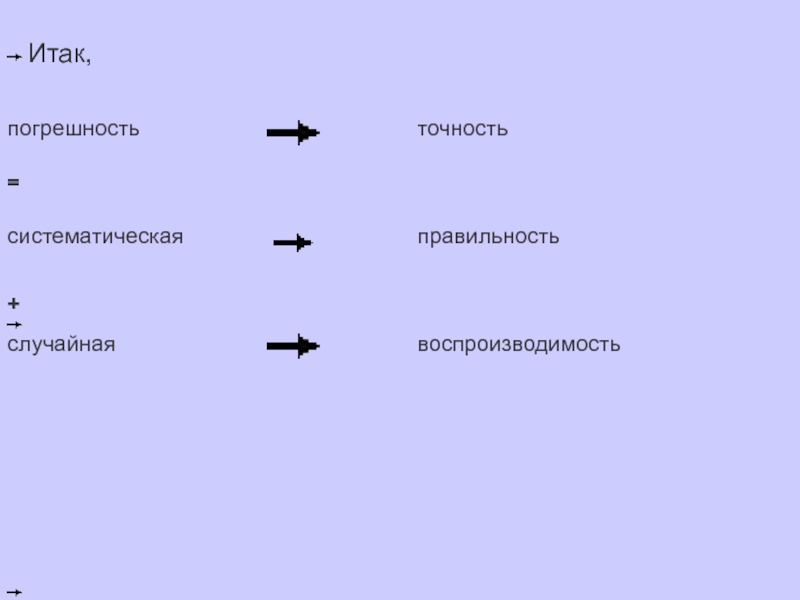
Слайд 15Точность (Достоверность) - характеризует малость погрешности (т.е. близость измеренной величины
к истинной)
Точность - общее понятие, которое включает в себя
Правильность
(систематическая погрешность) - метрологическая категория, характеризующая малость систематической составляющей погрешности. Иногда еще используется термин несмещенность
Воспроизводимость (случайная погрешность, или разброс относительно среднего) - характеризует малость случайной составляющей погрешности. Синоним - стабильность
Оценивают две составляющие погрешности по отдельности, эта общая оценка называется оценкой точности. При этом случайную погрешность (воспроизводимость) оценить проще, т.к. для этого не нужно знать истинное значение.
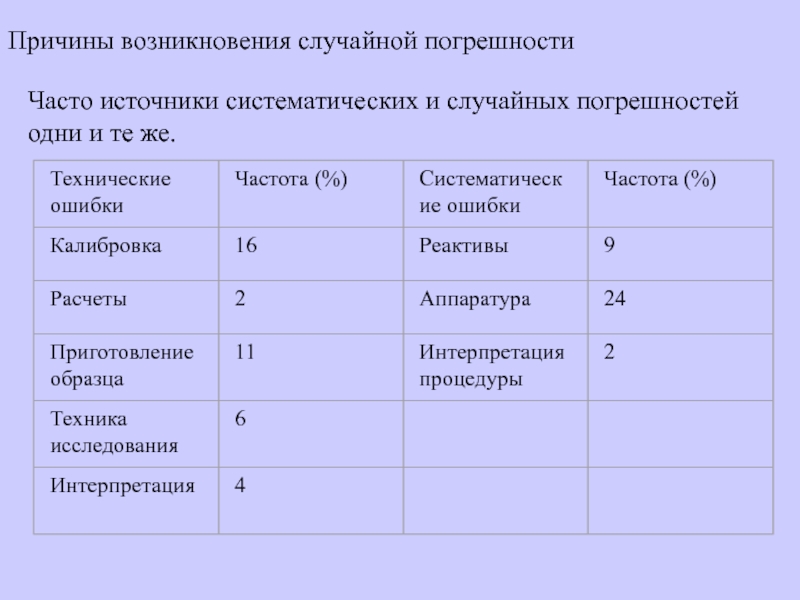
Слайд 17Причины возникновения случайной погрешности
Часто источники систематических и случайных погрешностей одни
и те же.
Слайд 18Основной вклад в общую погрешность вносят методические погрешности, в которые
входят
- погрешности отбора пробы (60 %), - переведение пробы
в удобную для анализа форму (например, сплавление и растворение),
- погрешности операции концентрирования и разделения компонентов (30 %);
- погрешности, обусловленные природой химической реакции, взятой в основу методики определения компонента;
- инструментальные погрешности или погрешности метода измерения составляют 10 %.
Слайд 19Случайная ошибка — одиночное значение, не выходящее за пределы установленной для данного
исследуемого компонента области, но стремящееся к выходу за эти пределы.
Случайные ошибки происходят при всяком измерении, и в том числе при любом аналитическом определении, как бы тщательно оно не проводилось. Наличие их сказывается в том, что при повторном определении того или иного элемента в данном образце, выполненном одним и тем же методом, дают, как правило, не одинаковые, а несколько различающиеся между собой результаты.
Они обусловлены:
1. свойствами самой пробы
2. некачественным инструментарием (неточностью пипеток, мерных колб, термоизмерительной аппаратуры, нестабильностью фотометрических приборов)
3. неточностью работы персонала лаборатории (неточное считываение результатов исследования, использование слишком которких шкал и.т.д.)
Слайд 20Случайные ошибки практически невозможно исключить совсем, но их можно значительно
ограничить после оценки размера ошибки. Чем меньше величина случайных ошибок
и меньше разброс индивидуальных показателей, тем лучше воспроизводимость лабораторных исследований. Случайные ошибки могут быть выявлены при постановке анализа в двух или больше параллельных пробах.
Для обработки случайных ошибок применяются методы математической статистики. Обычно при проведении химического анализа одного и того же объекта стараются получить от 3 до 7 результатов. Полученный числовой ряд называется выборочной совокупностью.
Слайд 21Способы оценки случайной погрешности
Для оценки случайной погрешности необходимо:
1. Оценить среднее
2.
Оценить разброс
Пусть есть n измерений, все измерения равноправны. Тогда
неизбежно
содержит погрешность, в том числе случайную (т.к. вычисляется из величин, содержащих погрешность)
Слайд 22Для оценки разброса необходимо ввести некоторые понятия:
Выборка (выборочная совокупность) -
конечное число значений одной случайной величины
Генеральная совокупность - полное (бесконечное)
множество значений. (т.е. она включает все возможные значения измеряемой величины и ничего добавить туда уже нельзя)
Функция плотности вероятности (или функция распределения) - по смыслу это относительная вероятность появления значения в генеральной совокупности.
Слайд 23Среднее для генеральной совокупности - точное (это константа и называется
она математическим ожиданием)
Слайд 24Мат. ожидание не равно истинному значению
эта разница как раз
характеризует систематическую погрешность:
причем -
мера систематической погрешности.
Для оценки воспроизводимости используются следующие характеристики:
Слайд 25f - число степеней свободы, f = n - k,
где k - число параметров, используемых при расчете (в данном
случае у нас одно уравнение связи - разброс вычисляется относительно среднего - следовательно, k = 1)
Число степеней свободы характеризует достоверность дисперсии.
Воспроизводимость зависит от условий (даже в пределах одной методики), от концентрации определяемого вещества, состава образца и т.д.
Слайд 26Для большинства метода величина Sr составляет порядка n*10-3 (десятые доли
%).
Е6сть методы с высокой воспроизводимостью, например, кулонометрия, где Sr составляет
порядка n*10-4
Большинство инструментальных методов характеризуются величиной Sr от 0,005 до 0,01.
Мет оды с более низкой воспроизводимостью относятся к полуколичественным. Они, как правило, обладают простой, эксперессностью и экономичностью и полезны для быстрой оценки состояния изучаемого объекта.
Слайд 27Оценка случайной погрешности
Дисперсии V(x) и стандартные отклонения S(x) сами по
себе не позволяют проводить вероятностную оценку случайной погрешности. Например, если
истинное значение определяемой концентрации= 10 мкг/мл, а стандартное отклонение - = 1 мкг/мл еще не значит, что среди результатов измерений не будет значений 8 мкг/мл, 12 мкг/мл и т.д.
Возникает задача вероятностной оценки погрешности
Слайд 28 Возможны три формулировки этой задачи:
1) Известно истинное значение и
интервал. Нужно найти вероятность того, что измеренное экспериментально значение попадет
в этот интервал.
2) Известно истинное значение и задана вероятность. Нужно найти интервал, в который измеренное значение попадает с этой вероятностью
3) Известно экспериментально измеренное значение и задана вероятность, нужно оценить интервал, в котором находится истинное значение с этой вероятностью.
Задача третьего типа имеет наибольшую практическую значимость, т.к. обычно истинное значение неизвестно, а экспериментратор располагает только измеренными значениями определяемой величины.
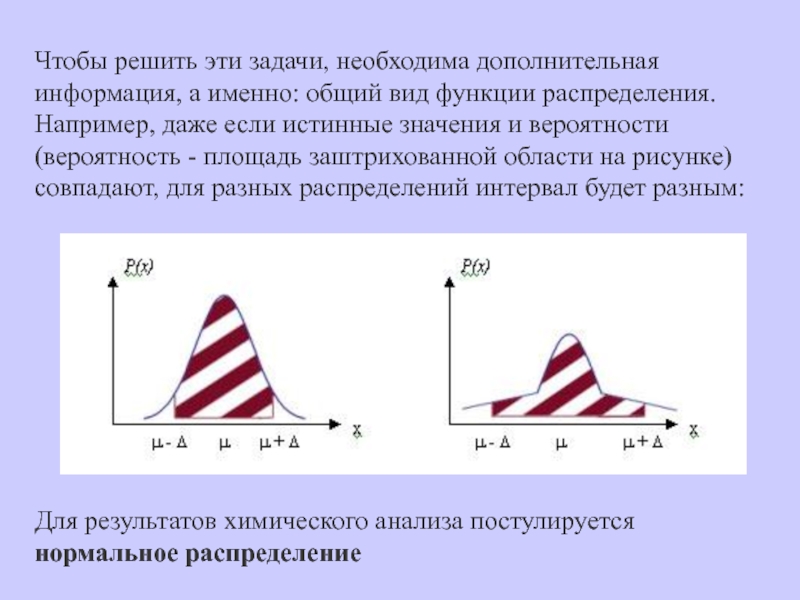
Слайд 29Чтобы решить эти задачи, необходима дополнительная информация, а именно: общий
вид функции распределения. Например, даже если истинные значения и вероятности
(вероятность - площадь заштрихованной области на рисунке) совпадают, для разных распределений интервал будет разным:
Для результатов химического анализа постулируется нормальное распределение
Слайд 30Доверительный интервал
, где t(p,f) - коэффициент Стьюдента при заданной доверительной
вероятности p (обычно принимается значение 95%) и числе степеней свободы
f.
тоже распределены по нормальному закону:
Слайд 31Т.о.
Величина
- это доверительный интервал, который используется в аналитической химии
для оценки воспроизводимости.
Слайд 32Причины возникновения систематической погрешности
Систематическими ошибками называют погрешности, одинаковые по признаку,
происходящие от определенных причин, влияющих на результаты либо в сторону
увеличения, либо в сторону уменьшения его. Систематические ошибки можно предусмотреть и устранить или же ввести соответствующие поправки. Наиболее характерными систематическими ошибками являются:
Слайд 33Методические ошибки: Они зависят от особенностей применяемого метода анализа, например,
от не вполне количественного протекания реакции, на которой основано определение,
от частичной растворимости осадка, от осаждения вместе с ним посторонних примесей, от течения наряду с основной реакцией каких-либо побочных реакций, искажающих результаты титриметрического определения, от свойств примененного при титровании индикатора и т.д. Методические ошибки составляют наиболее серьезную причину искажения результатов количественных определений, устранить их трудно.
Слайд 34- Ошибки, зависящие от применяемых приборов и реактивов. Это ошибки,
связанные с неравноплечностью или недостаточной точностью весов, с употреблением неповеренных
разновесов или сосудов для определения объемов, ошибки, происходящие в результате загрязнения раствора продуктами разрушения стекла, из которого сделана применяемая при анализе посуда.
- Ошибки оперативные. Они происходят от неправильного или недостаточно тщательного выполнения аналитических операций: недостаточное промывание осадков, приводящее к постоянному завышению результатов.
- Ошибки индивидуальные, зависящие от индивидуальных особенностей аналитиков, например, от его неспособности точно улавливать момент окраски при титровании и т.д.
Последние три вида систематических ошибок могут быть учтены и сведены до минимальных величин.
Слайд 35Систематические ошибки повторяются при каждом измерении, так как они вызываются
постоянными причинами. Поэтому они влияют на всю серию определений. Величина
систематической ошибки характеризует правильность результатов анализа.
Когда результаты отклоняются от истинного значения на постоянную величину, такая систематическая ошибка называется постоянной ошибкой. Она может вызываться неправильной холостой пробой, а также химической или спектральной интерференцией.
Когда ошибки между измеренной и истинной концентрацией пропорциональны концентрации вещества, систематическая ошибка называется пропорциональной ошибкой. Частая причина возникновения пропорциональной ошибки — это ошибочная калибровка.
Обнаружение и предупреждение систематических ошибок представляет собой сложную задачу.
Слайд 36Оценка правильности результатов анализа — проблема значительно более трудная, чем оценка воспроизводимости.
Для оценки воспроизводимости нам не надо иметь ничего, кроме серии
параллельных результатов измерения. Для оценки же правильности необходимо сравнение результата измерения с истинным значением. Такое значение никогда не может быть известно точно.
Слайд 37Способы количественной оценки правильности (систематической погрешности)
Систематическая погрешность
Таким образом, чтобы
найти , нужно сопоставить
с
Здесь возникают две проблемы:
1) с чем сравнивать? (где взять ?)
2) как сравнивать?
Слайд 381) сравнивают с арбитражным значением , полагают, что
~
Требования:
-
не содержит погрешности
- случайная погрешность меньше случайной погрешности результатов
Способы получения :
- независимый анализ (более точной методикой, а лучше другим методом)
- введено-найдено (по существу сравнение с гравиметрией)
- анализ стандартных образцов - самый надежный способ
Слайд 392) Действительное значение измеряемой величины - это (систематическая и случайная
погрешности пренебрежимо малы) - постулируется, как
Обозначается a(x) = const
Но
у нас нет , есть , которое содержит случайную погрешность. Чем обусловлена разница между и a - случайной или систематической погрешностью? Случайную погрешность на фоне систематической обнаружить легко. Систематическую на фоне случайной - сложно. Поэтому если неравенство можно объяснить случайной погрешностью, считается, что систематической погрешности нет ("презумпция правильности").
Слайд 40Выявление систематической погрешности
1. Если есть значение a:
сравниваем
и a(x) , т.е. попадает ли a в доверительный интервал.
где
t - табличное значение критерия Стьюдента при заданной доверительной вероятности p (обычно полагается равной 0.95) и числе степеней свободы f = n-1
Если < - нет систематической погрешности, если > - есть
Слайд 412. Значение a недоступно.
сравниваем и
, каждое распределено по нормальному закону.
Условие:
Т.о. сначало нужно сравнивать
дисперсии. Но они не подчиняются нормальному распределению, для них не подходит t-критерий.
Существует критерий Фишера:
Слайд 42Если >, то различие в воспроизводимости существенно, нельзя сравнивать.
Если
то усредняем дисперсии с учетом весомости:
и сравниваем:
причем
Слайд 43Оперативный контроль точности
Проверка годности реактивов
Слайд 44Способы проверки и повышения правильности
· Лекции
1. Варьирование размеров
пробы
Предпосылки: Систематическая погрешность =const (такая погрешность называется аддитивной), т.е. измеренное
количество вещества связяно с истинным содержанием такой формулой:
nизм = nист +
Тогда сизм = сист + / V, где V - объем пробы.
Закономерное изменение сизм в зависимости от объема пробы говорит о наличии аддитивной погрешности.
Слайд 45Однако не всякая систематическая погрешность является аддитивной. Существуют погрешности другого
типа, величина которых прямо пропорциональна размеру пробы (или содержанию определяемого
компонента). Такие погрешности называются мультипликативными. Они увеличивают или (чаще) уменьшают значение аналитического сигнала в одно и то же число раз, т.е. изменяют наклон градуировочной зависимости. Очевидно, что такие систематические погрешности описанный способ выявить не может. В то же время мультипликативные систематические погрешности можно значительно уменьшить с помощью специального способа градуировки, называемого способом добавок.
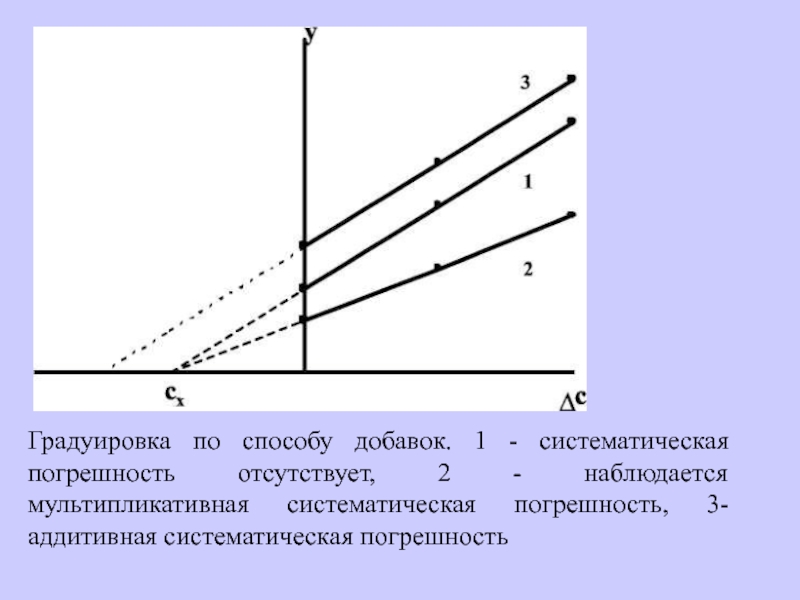
Слайд 46Градуировка по способу добавок. 1 - систематическая погрешность отсутствует, 2
- наблюдается мультипликативная систематическая погрешность, 3- аддитивная систематическая погрешность
Слайд 47Основная цель способа добавок — беспечение максимально точного соответствия условий градуировки и
собственно определения. При использовании способа добавок эти две операции совмещаются
воедино: известные содержания определяемого компонента вводят как добавки непосредственно в анализируемый раствор и представляют градуировочную функцию в виде графика зависимости аналитического сигнала от концентрации добавки Ас (рис.). Содержание компонента в анализируемом растворе находят путем экстраполяции полученной зависимости на нулевое (или фоновое, если оно известно) значение аналитического сигнала. Легко видеть, что в этом случае даже при наличии мультипликативной погрешности (т.е. изменении тангенса угла наклона градуировочного графика) получается правильный результат (ср. кривые 1 и 2 рис.). В то же время аддитивную систематическую погрешность способ добавок устранить не может (кривая 3 рис.).
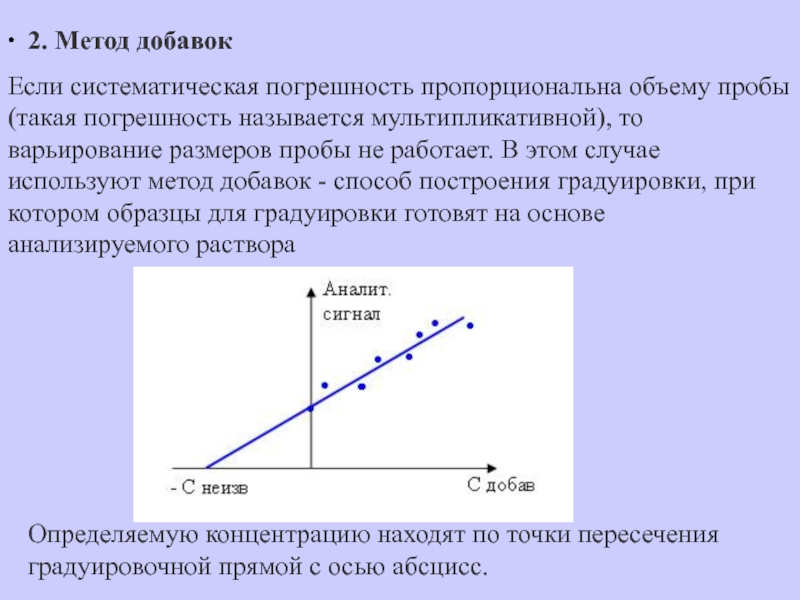
Слайд 48· 2. Метод добавок
Если систематическая погрешность пропорциональна объему пробы (такая погрешность
называется мультипликативной), то варьирование размеров пробы не работает. В этом
случае используют метод добавок - способ построения градуировки, при котором образцы для градуировки готовят на основе анализируемого раствора
Определяемую концентрацию находят по точки пересечения градуировочной прямой с осью абсцисс.
Слайд 493. Релативизация
Релативизация - взаимная компенсация погрешностей. Если погрешность аддитивная, то
она компенсируется вычитанием. Например, при взвешивании масса вещества вычисляется по
разности массы тары с веществом и массы пустой тары. В этом случае аддитивная погрешность весов компенсируется.
Если погрешность мультипликативная, она компенсируется делением: например, в методе внутреннего стандарта (наиболее часто используется в хроматографии).
4. Метод внутреннего стандарта - метод градуировки, при котором в качестве аналитического сигнала испльзуется отношение сигнала определяемого вещества и сигнала стандарта - это позволяет компенсировать мультипликативную погрешность.
Слайд 504. Рандомизация
Строгий контроль условий измерений уменьшает случайную погрешность, но увеличивает
"риск" систематической погрешности. Выход: перебрать как можно больше условий измерений
(выбранных случайным образом), тогда систематическая погрешность перейдет в случайную, выявлять которую проще. (Погрешность не исчезает, а просто переходит в другую форму).
Недостатки:
1) Необходим большой массив данных
2) Высокая случайная погрешность. Ее можно уменьшить опять же за счет увеличения числа измерений.
Метод рандемизации используется при аттестации стандартов (когда один образец анализирует несколько лабораторий, разными методами и т.д.)
Слайд 51Грубые критерии. Эти критерии определяют, есть ли резко выпадающие данные
(грубые ошибки, промахи, выбросы). Эти критерии не рассматривают всей совокупности
данных, а только крайние значение. Примером может служить Q-критерий. Тестовая статистика Q-критерия вычисляется по формуле:
где x? - "подозрительное" значение (вероятный промах) - это максимальное или минимальное значение выборки, xближайшее - ближайшее к подозрительному значение, xмин и xмакс - максимальное и минимальное значения выборки (эта формула верна для числа измерений n = 3..7. При n = 8..10 в знаменателе должна стоять разница между подозрительным значением и ближайшем к максимальному (или минимальному)).
Слайд 52Значение Q сравнивают с табличным значением, и если табличное значение
критерия меньше тестовой статистики, то подозрительный результат является промахом и
исключается из дальнейшего рассмотрения. При этом обычно доверительную вероятность берут равной 0.90, а не 0.95. В данном случае это является некоторым "ужесточением" требований: лучше выбросить значение, не являющееся промахом, чем оставить промах в выборке. Как правило, на промах проверяют минимальное и максимальное значение выборки.
Q-критерий работает для выборок, содержащих 3 - 10 значений, при больших объемах выборки он становится нечувствителен к промахам.
Слайд 58Основные характеристики чувствительности
1. Коэффициент чувствительности S
Показывает, насколько сильно меняется
сигнал при изменении концентрации. В случае, если градуировочная функция -
прямая, коэффициент чувствительности
S = tg(a), где а - угол наклона прямой.
В общем же случае коэффициент чувствительности зависит от концентрации и вычисляется как производная аналитического сигнала по концентрации:
Слайд 59недостатки:
1) коэффициент чувствительности имеет размерность, его нельзя сопоставить для разных
методов
2) не учитывает различие в воспроизводимости (высокий коэффициент чувствительности при
низкой воспроизводимости бесполезен)
Слайд 60Проверка статистической гипотезы
Статистическая гипотеза - некоторое предположение о законе
распределения случайной величины или о параметрах этого закона в рамках
данной выборки.
Пример статистической гипотезы: "генеральная совокупность распределена по нормальному закону", "различие между дисперсиями двух выборок незначимо" и т.д.
При аналитических расчетах часто необходимо выдвигать и проверять гипотезы. Проверка статистической гипотезы осуществляется с помощью статистического критерия в соответствии со следующим алгоритмом:
Слайд 61Метод проверки статистической гипотезы:
1. Формулировка гипотезы
Гипотеза формулируется в терминах различия
величин. Например, есть случайная величина x и константа a. Они
не равны (арифметически), но нужно установить, значимо ли статистически между ними различие?
Существует два типа критериев:
1) двухсторонний критерий вида:
2) односторонний критерий вида: или
Необходимо отметить, что знаки >, <, = здесь используются не в арифметическом, а в "статистическом" смысле. Их необходимо читать "значимо больше", "значимо меньше", "различие незначимо".
Слайд 622. Установка закона распределения
Далее необходимо установить или постулировать закон распределения.
Подробнее о проверке вида распределения - в следующих лекциях.
Существуют
также критерии, которые не зависят от вида распределения - так называемые непараметрические критерии.
3. Вычисление тестовой статистики
Тестовая статистика - некоторая функция от рассматриваемых величин, закон распределения которой точно известен и ее можно сравнить с табличным значением. Например, при сравнении двух дисперсий по критерию Фишера тестовая статистика вычисляется по следующей формуле:
Слайд 634. Сравнение с табличным значением
Затем тестовая статистика сравнивается с табличным
значением
Тестовая статистика всегда зависит от доверительной вероятности, и, в
некоторых случаях, от дополнительных параметров. Так, в приведенном выше примере сравнения двух дисперсий тестовая статистика сравнивается с табличным значением критерия Фишера ("критическим" значением), которое зависит от доверительной вероятности p и числа степеней свободы дисперсий f1 и f2.
5. Вывод
На основании сравнения делается вывод о том, выполняется ли гипотеза (например, значимо ли различие и т.д.)
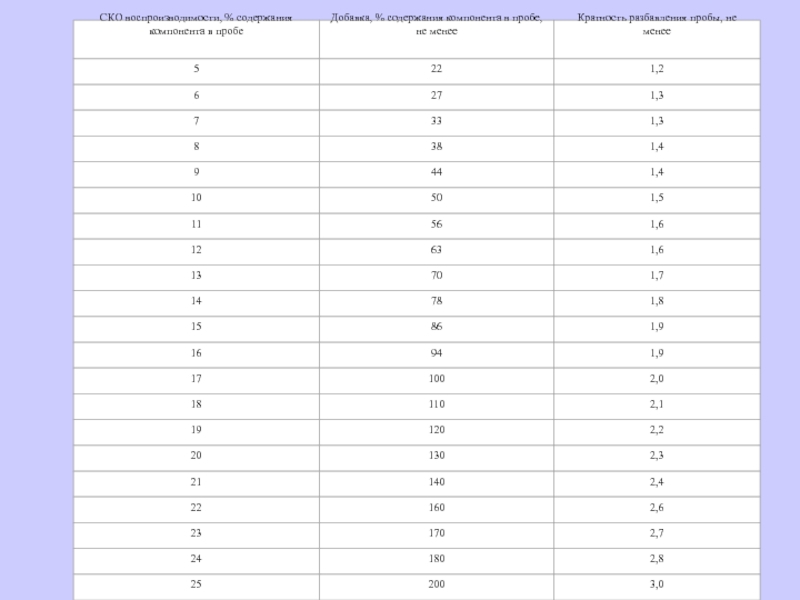
Слайд 64РМГ 61—2003
ПОКАЗАТЕЛИ ТОЧНОСТИ, ПРАВИЛЬНОСТИ, ПРЕЦИЗИОННОСТИ МЕТОДИК КОЛИЧЕСТВЕННОГО ХИМИЧЕСКОГО АНАЛИЗА. Методы
оценки
Приложение И
(рекомендуемое)
Добавка к пробе (разбавленной пробе) и кратность разбавления
в зависимости
от СКО воспроизводимости
Слайд 66Метод стандартов и метод добавок применимы для линейной градуировочной функции.
Метод градуировочного графика допускает использование как линейной, так и нелинейной
функций аналитический сигнал — содержание. В последнем случае требуется большее число экспериментальных данных и результат определения содержания компонента бывает, как правило, менее точным.
При проведении химического анализа обычно не ограничиваются единичным определением, а проводят, как правило, 3–5 параллельных определений для одной и той же пробы или стандартного образца в одинаковых условиях.
Средний результат параллельных определений называется результатом анализа (С или ). Отклонение результата анализа от истинного содержания определяемого вещества () в образце называют погрешностью определения. Поэтому, наряду с определением содержания вещества важна оценка достоверности результатов измерений.