задача о шестиугольной призме в ЕГЭ

равна 5, а высота — 10.
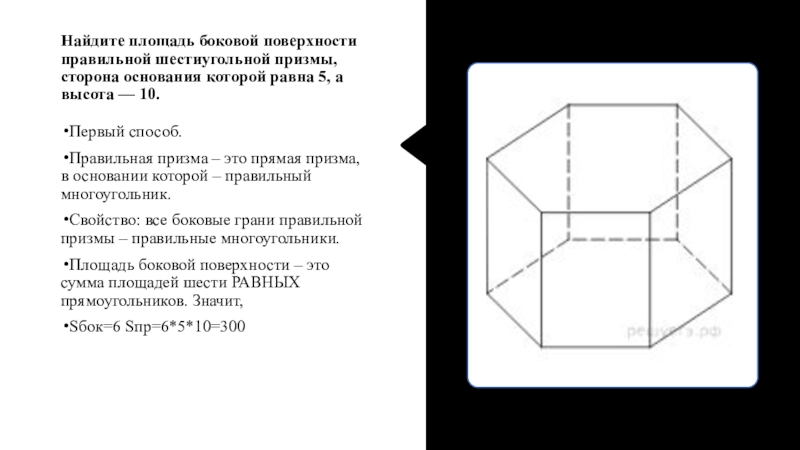
Первый способ.
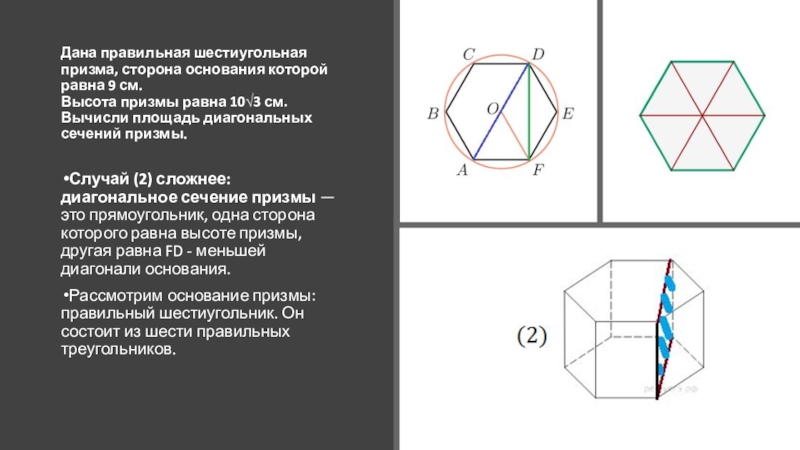
Правильная призма – это

прямая призма, в основании которой – правильный многоугольник.
Свойство: все боковые грани правильной призмы – правильные многоугольники.
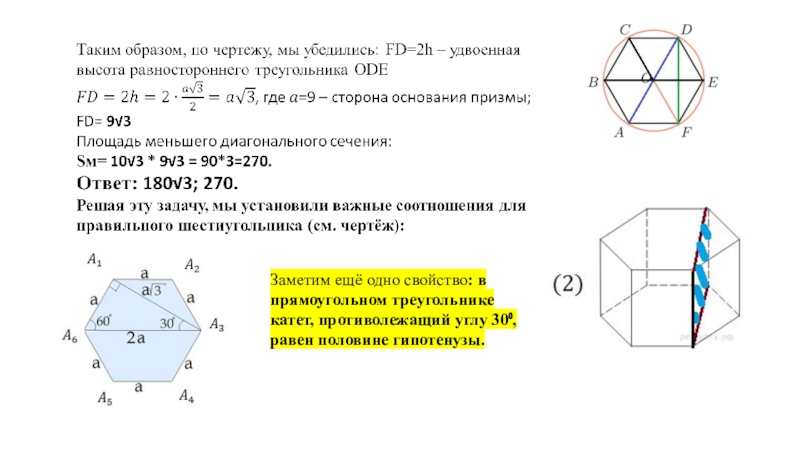
Площадь боковой поверхности – это сумма площадей шести РАВНЫХ прямоугольников. Значит,
Sбок=6 Sпр=6*5*10=300

равна 5, а высота — 10.
Второй способ.
Правильная призма – это

прямая призма, в основании которой – правильный многоугольник.
Площадь боковой поверхности для прямой и, в частности, правильной призмы можно найти по формуле: Sбок=Росн*h
Периметр основания:
Росн=5+5+5+5+5+5=6*5=30
Sбок=30*10=300

Вычисли площадь диагональных сечений призмы.
Диагональ многогранника – отрезок, соединяющий две вершины,

не принадлежащие одной грани.
Диагональное сечение призмы — это сечение плоскостью, проходящей через два боковых ребра, не принадлежащие одной грани.
Диагональное сечение призмы — это сечение, которое проходит через диагональ основания и диагональ призмы. Т.к. боковые ребра призмы параллельны и равны, то диагональное сечение призмы - параллелограмм. Если призма прямая - то прямоугольник.

Вычисли площадь диагональных сечений призмы.
Случай (1) – простой: диагональное сечение

призмы — это прямоугольник, одна сторона которого равна высоте призмы, другая равна AD - большей диагонали основания.
Рассмотрим основание: правильный (выпуклый, все стороны равны, все угла равны) шестиугольник. Его сторона равна радиусу описанной окружности: AB=OF=R
Большая диагональ: AD=2R=2*9=18
Площадь большего сечения: Sб= 10√3 * 18 = 180√3

Вычисли площадь диагональных сечений призмы.
Случай (2) сложнее: диагональное сечение призмы —

это прямоугольник, одна сторона которого равна высоте призмы, другая равна FD - меньшей диагонали основания.
Рассмотрим основание призмы: правильный шестиугольник. Он состоит из шести правильных треугольников.

30⁰, равен половине гипотенузы.