Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи с решениями по теории вероятности для 11 класса при подготовке к ЕГЭ
Содержание
- 1. Задачи с решениями по теории вероятности для 11 класса при подготовке к ЕГЭ
- 2. В некоторой местности наблюдения показали:
- 3. Решение.Найдем вероятность того, что утро пасмурное и
- 4. Если гроссмейстер А. играет белыми, то он
- 5. Решение.Событие Х - "Играя белыми одну партию,
- 6. Две фабрики выпускают одинаковые стекла для автомобильных
- 7. Решение. Переводим %% в дроби.Событие А -
- 8. Вероятность того, что батарейка бракованная, равна
- 9. Решение. Вероятность того, что взятая наугад
- 10. Автоматическая линия изготавливает
- 11. Решение. Вероятность, что готовая батарейка исправна равна 1-0,02=0,98
- 12. Вероятности того, что деталь определенного типа
- 13. Решение. Не более, чем в 3-х ящиках
- 14. Вероятность того, что взятая наугад деталь
- 15. Решение. Вероятность, что деталь бракованная равна 0,2,
- 16. На рисунке изображён лабиринт. Паук заползает в
- 17. Решение. На первом разветвлении у паука 2
- 18. Механические часы с двенадцатичасовым циферблатом в какой‐то
- 19. Решение. Благоприятный диапазон - 3 промежутка (10-11,
- 20. На рисунке изображён лабиринт. Паук заползает
- 21. Решение. На каждом разветвлении вероятность выбора направления
- 22. Всем пациентам с подозрением на гепатит делают
- 23. Решение. Вероятность того, что поступивший болен гепатитом равна
- 24. В группе туристов 5 человек. С помощью
- 25. Решение. Исход - выбор 2-х человек из
- 26. Перед началом футбольного матча судья бросает
- 27. Решение. В одной игре команда "Физик" имеет
- 28. Ковбой Джон попадает в муху на стене
- 29. Решение. Вероятность того, что пистолет пристрелянный равна
- 30. При артиллерийской стрельбе автоматическая система делает выстрел
- 31. Решение. Вероятность поразить мишень равна сумме вероятностей
- 32. Чтобы пройти в следующий круг соревнований, футбольной
- 33. Решение. 4 очка и больше в двух
- 34. Скачать презентанцию
В некоторой местности наблюдения показали: Если июньское утро ясное, то вероятность дождя в этот день 0,1. Если июньское утро пасмурное, то вероятность дождя в течение дня равна 0,4. Вероятность
Слайды и текст этой презентации
Слайд 2 В некоторой местности наблюдения показали: Если июньское утро ясное, то вероятность
дождя в этот день 0,1. Если июньское утро пасмурное, то вероятность
дождя в течение дня равна 0,4. Вероятность того, что утро в июне будет пасмурным, равна 0,3. Найдите вероятность того, что в случайно взятый июньский день дождя не будет.Слайд 3Решение.
Найдем вероятность того, что утро пасмурное и дождя не будет
или утро ясное и дождя не будет.
0,3*(1- 0,4) + 0,7(1-0,1)
= 0,3*0,6 + 0,7*0,9 = 0,18+0,63 = 0,81Слайд 4Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера
Б. с вероятностью 0,6.
Если А. играет черными, то А.
выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.Слайд 5Решение.
Событие Х - "Играя белыми одну партию, А. выигрывает".
Событие У
- "Играя черными одну партию, А. выигрывает".
Рассмотрим событие (Х и
У).Р(Х и У) = Р(Х)*Р(У) = 0,6*0,4=0,24.
Ответ: 0,24
Слайд 6Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
выпускает 30% этих стекол, вторая — 70%. Первая фабрика выпускает
3% бракованных стекол, а вторая — 4%. Найдите вероятность того, что случайно купленное в магазине стекло, окажется бракованным.Слайд 7Решение.
Переводим %% в дроби.
Событие А - "Куплены стекла
первой фабрики". Р(А)=0,3
Событие В - "Куплены стекла второй фабрики". Р(В)=0,7
Событие
Х - " Стекла бракованные".Р(А и Х) = 0.3*0.03=0.009
Р(В и Х) = 0.7*0.04=0.028
По формуле полной вероятности:
Р = 0.009+0.028 = 0.037
Ответ: 0,037
Слайд 8 Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в
магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите
вероятность того, что обе батарейки окажутся исправными.Слайд 9Решение. Вероятность того, что взятая наугад батарейка исправна, равна
1-0,06 = 0,94
Р = 0,94*0,94 - вероятность, что и первая
и вторая исправныОтвет: 0,8836
Слайд 10 Автоматическая линия изготавливает батарейки. Вероятность того,
что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка
проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная из упаковки батарейка будет забракована.Слайд 11Решение.
Вероятность, что готовая батарейка исправна равна 1-0,02=0,98
Р1= 0,02*0,99 =
0,0198 - вероятность, что неисправную батарейку забракуют
Р2= 0,98*0,01 = 0,0098
- вероятность, что исправная батарейка будет забракованаР=Р1+Р2 = 0,0296
Ответ: 0,0296
Слайд 12 Вероятности того, что деталь определенного типа находится в первом,
втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8,
0,9. Найти вероятности того, что эта деталь находится не более, чем в трех ящиках.Слайд 13Решение. Не более, чем в 3-х ящиках означает, что деталь
находится в одном, двух или трех ящиках. Противоположное событие -
деталь находится во всех четырех ящиках. Найдем вероятность этого противоположного события.Р1 = 0,6*0,7*0,8*0,9 = 0,3024, тогда Р = 1- Р1 = 1 - 0,3024 = 0,6976
Ответ: 0,6976
Слайд 14 Вероятность того, что взятая наугад деталь из некоторой партии
деталей, будет бракованной равна 0,2. Найти вероятность того,
что из трех взятых деталей 2 окажутся не бракованными.Слайд 15Решение.
Вероятность, что деталь бракованная равна 0,2, что деталь без
брака равна 1-0,2=0,8.
Р1= 0,2*0,8*0,8 = 0,128 - вероятность того, что
первая деталь бракованная, а вторая и третья нет.Р2=0,8*0,23*0,8 = 0,128 - вторая бракованная, аналогично Р3=0,128 - третья бракованная.
Р = Р1+Р2+Р3 = 3*0,128 = 0,384
Ответ: 0,384
Слайд 16На рисунке изображён лабиринт. Паук заползает в лабиринт в точке
«Вход».
Развернуться и ползти назад паук не может. На каждом разветвлении
паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным,определите, с какой вероятностью паук придёт к выходу D.
Слайд 17Решение.
На первом разветвлении у паука 2 исхода, вероятность каждого
1/2. С вероятностью 0,5 он поползет к выходу D.
Ответ: 0,5
Слайд 18Механические часы с двенадцатичасовым циферблатом в какой‐то момент сломались и
перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув
отметки 10, но не дойдя до отметки 1 час.Слайд 19Решение.
Благоприятный диапазон - 3 промежутка (10-11, 11-12, 12-1), весь
диапазон - 12 промежутков.
Р = 3/12 =1/4=0,25
Ответ: 0,25
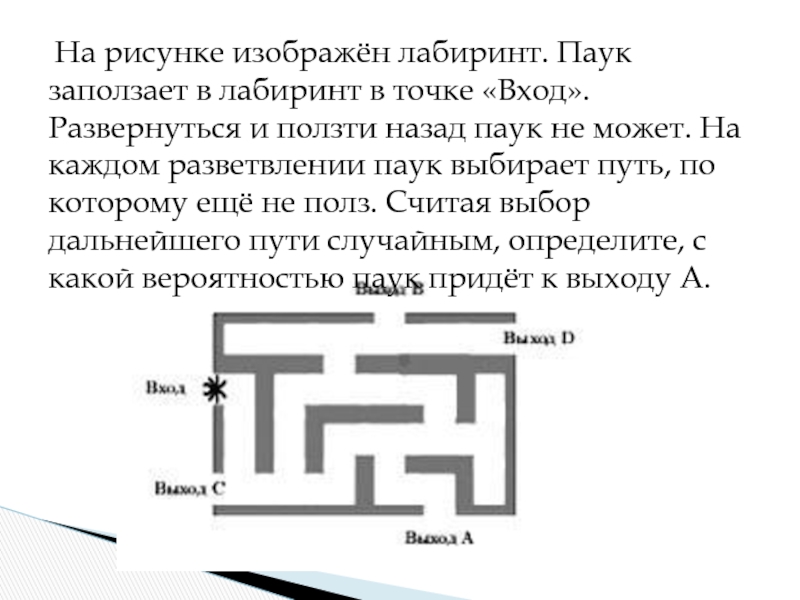
Слайд 20 На рисунке изображён лабиринт. Паук заползает в лабиринт в
точке «Вход». Развернуться и ползти назад паук не может. На
каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу А.Слайд 21Решение.
На каждом разветвлении вероятность выбора направления равна 0,5. К
выходу А есть 2 пути. На одном - паук делает
выбор 5 раз, а на втором - 3 раза, с вероятностью 0,5 каждый раз.Р = 0,55 +0,53 = 0,53(0,25+1) = 0,125*1,25 = 0,15625
Ответ: 0,15625
Слайд 22Всем пациентам с подозрением на гепатит делают анализ крови. Если
анализ выявляет гепатит, то результат анализа называется положительным. У больных
гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Еслипациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным
Слайд 23Решение.
Вероятность того, что поступивший болен гепатитом равна 0,05, а что
не болен - равна 0,95.
Р= 0,05*0,9 + 0,95*0,01 = 0,0545
Слайд 24В группе туристов 5 человек. С помощью жребия они выбирают
двух человек, которые должны идти в село за продуктами. Турист
А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?Слайд 25Решение. Исход - выбор 2-х человек из 5. Количество исходов
С52 = 5!/(2!*3!) = 5*4/2 = 10.
Благоприятный исход: Турист А
с кем-то в паре. Таких исходов 4.Р = 4/10 = 0,4
Слайд 26 Перед началом футбольного матча судья бросает монетку, чтобы определить,
какая из команд начнёт игру с мячом. Команда «Физик» играет
три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.Слайд 27Решение. В одной игре команда "Физик" имеет 2 исхода: начинает
игру или начинает не она. Т.к. игр три, то всего
исходов 23=8.Будем обозначать благоприятный исход - 1, не благоприятный 0.
Для трех игр расстановка исходов такая:
000, 001, 010, 011, 100, 101, 110, 111.
Среди них благоприятных 3: 011, 101, 110.
Р=3/8 = 0,375.
Слайд 28Ковбой Джон попадает в муху на стене с вероятностью 0,9,
если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного
револьвера, то он попадает в муху с вероятностью 0,2.На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Слайд 29Решение.
Вероятность того, что пистолет пристрелянный равна 0,4, что нет
- 0,6.
Вероятность попасть в муху из пистолета, если он пристрелянный,
равна 0,4*0,9=0,36.Вероятность попасть в муху, если пистолет непристрелянный, равна 0,6*0,2=0,12.
Вероятность промаха Р=1-0,48=0,52
Слайд 30При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если
цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются
до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?Слайд 31Решение.
Вероятность поразить мишень равна сумме вероятностей поразить её при
первом или втором или ... k-м выстреле.
Будем вычислять вероятность уничтожения
при k-м выстреле, задавая значения k=1,2,3... И суммируя полученные вероятностиk=1 P=0,4 S=0,4
k=2 P=0,6*0,6=0,36 - при первом выстреле промах, при втором цель уничтожена
S=0,4+0,36=0,76
k=3 P=0,6*0,4*0,6 = 0,144 - цель уничтожена при третьем выстреле
S=0,76+0,144=0,904
k=4 P=0,6*0,4*0,4*0,6= 0,0576 - при 4-м
S=0,904+0,0576=0,9616
k=5 P=0,6*0,43*0,6 = 0,02304
S=0,9616+0,02304=0,98464 - достигли нужной вероятности при k=5.
Ответ: 5.
Слайд 32Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать
хотя бы 4 очка в двух играх. Если команда выигрывает,
она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.Слайд 33Решение. 4 очка и больше в двух играх можно набрать
такими способами:
3+1 выиграла, ничья
1+3 ничья, выиграла
3+3
оба раза выигралаВероятность выигрыша равна 0,4, проигрыша - 0,4, вероятность ничьей равна 1-0,4-0,4 = 0,2.
Р = 0,4*0,2 + 0,2*0,4 + 0,4*0,4 = 2*0,08+0,16 = 0,32
Ответ: 0,32