Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Закон Джоуля –Ленца Законы Кирхгофа
Содержание
- 1. Закон Джоуля –Ленца Законы Кирхгофа
- 2. Закон Джоуля-ЛенцаОднородный участок цепи
- 3. Неоднородный участок цепи
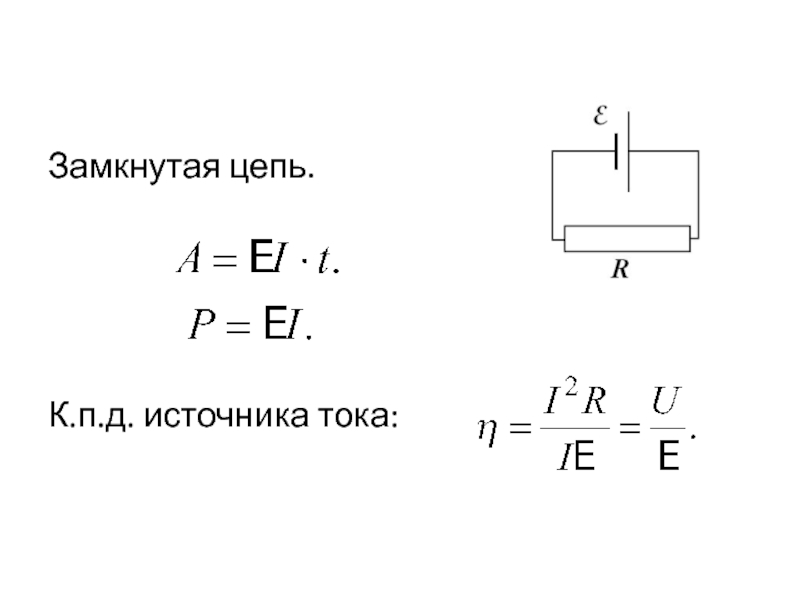
- 4. Замкнутая цепь.К.п.д. источника тока:
- 5. Закон Джоуля-Ленца в дифференциальной формеУдельная тепловая мощность
- 6. Закон Джоуля-Ленца в дифференциальной форме
- 7. Законы КирхгофаИспользуются для расчета разветвленных цепей постоянного
- 8. Узел электрической цепи – точка разветвленной цепи,
- 9. Первый закон Кирхгофа (следствие закона сохранения заряда):
- 10. Второй закон Кирхгофа (обобщенный закон Ома): в
- 11. Второй закон КирхгофаТок считается положительным, если его
- 12. Порядок расчета разветвленной цепи:1. Произвольно выбрать и
- 13. 3. Выделить произвольно замкнутые контуры в цепи,
- 14. Магнитное поле.
- 15. Магнитные явления были известны еще в древнем
- 16. Первыми экспериментами, показавшими, что между электрическими и
- 17. В 1820 году французский физик А. Ампер
- 18. Тогда полная электромагнитная сила, действующая на заряд
- 19. Если заряженная частица движется в однородном магнитном
- 20. Период обращения частицы в однородном магнитном поле
- 21. Циклотронная частота не зависит от скорости частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц..
- 22. Если частица влетает в магнитное поле не
- 23. Источниками магнитного поля являются движущиеся электрические
- 24. В результате обобщения экспериментальных данных был получен
- 25. Магнитное поле постоянных токов
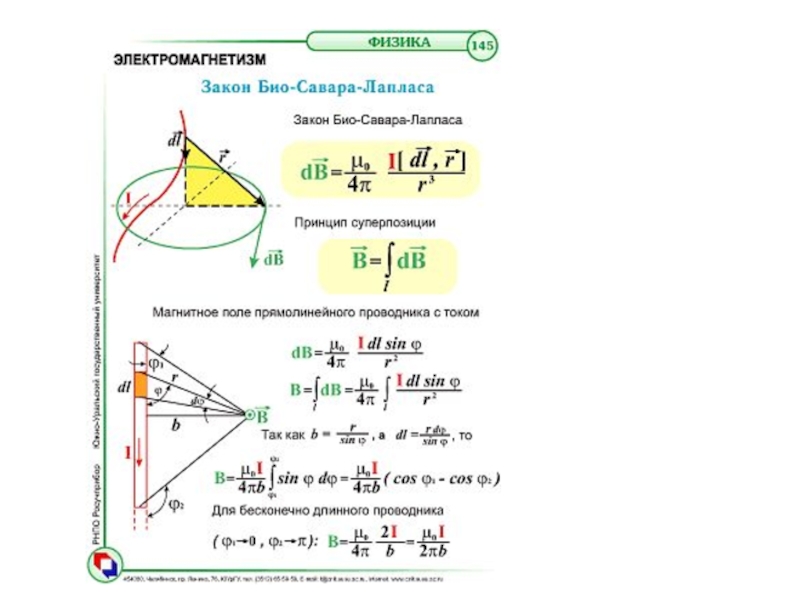
- 26. Закон Био-Савара-Лапласа Элементарный заряд q равен
- 27. Магнитное поле создаваемое линейным элементом тока выглядит
- 28. Слайд 28
- 29. Слайд 29
- 30. Как и любое другое векторное
- 31. Магнитное поле обладает, как и электрическое поле,
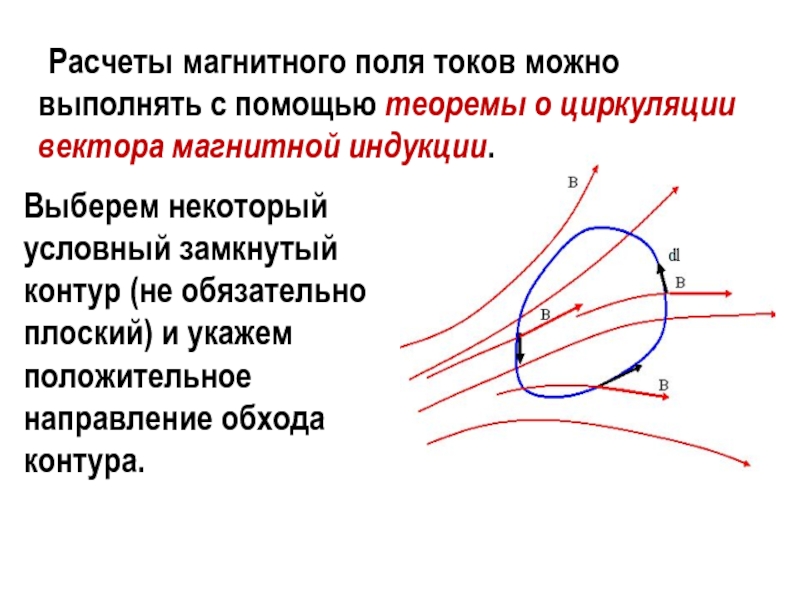
- 32. Расчеты магнитного поля токов
- 33. Теорема о циркуляция вектора
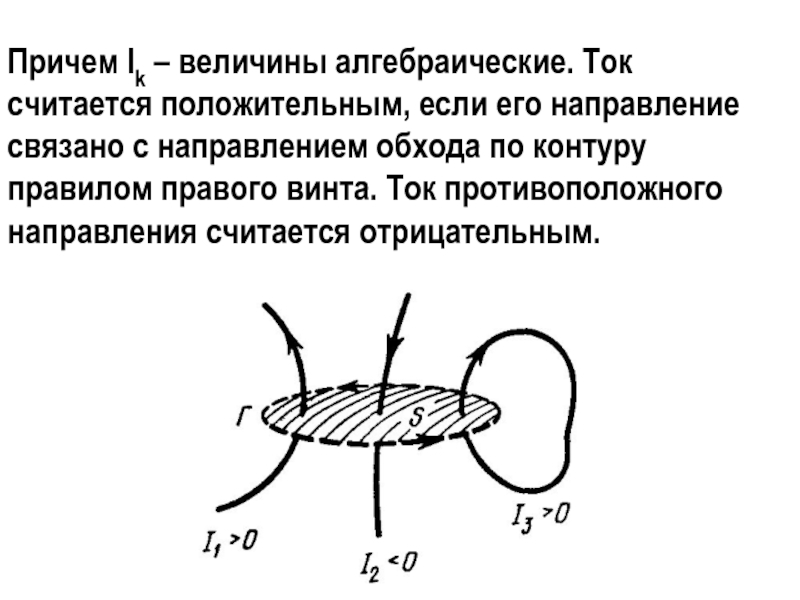
- 34. Причем Ik – величины алгебраические. Ток считается
- 35. Контрольные вопросыЗакон Джоуля-Ленца в интегральной и дифференциальной формеМощность токаЗаконы КирхгофаСила ЛоренцаПоток и циркуляция вектора магнитной индукции.
- 36. Слайд 36
- 37. Скачать презентанцию
Закон Джоуля-ЛенцаОднородный участок цепи
Слайды и текст этой презентации
Слайд 5Закон Джоуля-Ленца в дифференциальной форме
Удельная тепловая мощность тока – количество
тепла, выделившееся в единичном объеме за единицу времени.
Слайд 7Законы Кирхгофа
Используются для расчета разветвленных цепей постоянного тока.
Неразветвленная электрическая цепь
– цепь, в которой все элементы цепи соединены последовательно.
Элемент электрической
цепи – любое устройство, включенное в электрическую цепь.
Слайд 8Узел электрической цепи – точка разветвленной цепи, в которой сходится
более двух проводников.
Ветвь разветвленной электрической цепи – участок цепи между
двумя узламиЗаконы Кирхгофа
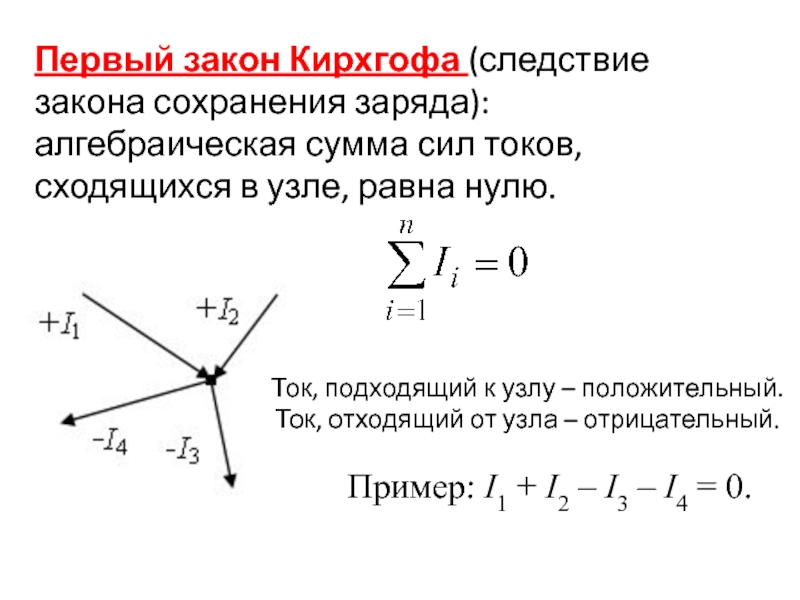
Слайд 9Первый закон Кирхгофа (следствие закона сохранения заряда): алгебраическая сумма сил
токов, сходящихся в узле, равна нулю.
Пример: I1 + I2 – I3 – I4 = 0.
Ток, подходящий к
узлу – положительный.Ток, отходящий от узла – отрицательный.
Слайд 10Второй закон Кирхгофа
(обобщенный закон Ома): в любом замкнутом контуре,
произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил
токов Ii на сопротивление соответствующих участков Ri этого контура равна алгебраической сумме э.д.с. в контуре.
Слайд 11Второй закон Кирхгофа
Ток считается положительным, если его направление совпадает с
условно выбранным направлением обхода контура.
Э.д.с. считается положительной,
если направление обхода
происходит от – к + источника
тока, т.е. э.д.с. создает ток,
совпадающий с направлением обхода.
Слайд 12Порядок расчета разветвленной цепи:
1. Произвольно выбрать и обозначить на чертеже
направление тока во всех участках цепи.
2. Подсчитать число узлов в
цепи (m). Записать первый закон Кирхгофа для каждого из (m-1) узлов.
Слайд 133. Выделить произвольно замкнутые контуры в цепи, произвольно выбрать направления
обхода контуров.
4. Записать для контуров второй закон Кирхгофа. Если цепь
состоит из р-ветвей и m-узлов, то число независимых уравнений 2-го закона Кирхгофа равно ( p-m+1 ). 
Слайд 15Магнитные явления были известны еще в древнем мире. Компас был
изобретен более 4500 лет тому назад.
Он появился в Европе приблизительно
в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.
Слайд 16Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется
глубокая связь, были опыты датского физика Х. Эрстеда (1820 г.). Эти
опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку
Слайд 17В 1820 году французский физик А. Ампер установил закон взаимодействия
токов.
Проводники с током оказывают силовое действие друг на друга
не непосредственно, а через окружающие их магнитные поля. Все свойства магнитной силы можно описать, если ввести понятие магнитного поля.
Это поле характеризуется магнитной индукцией В.
Слайд 18Тогда полная электромагнитная сила, действующая на заряд q:
Эту силу называют
силой Лоренца. Она состоит из электрической и магнитной составляющих.
Магнитное
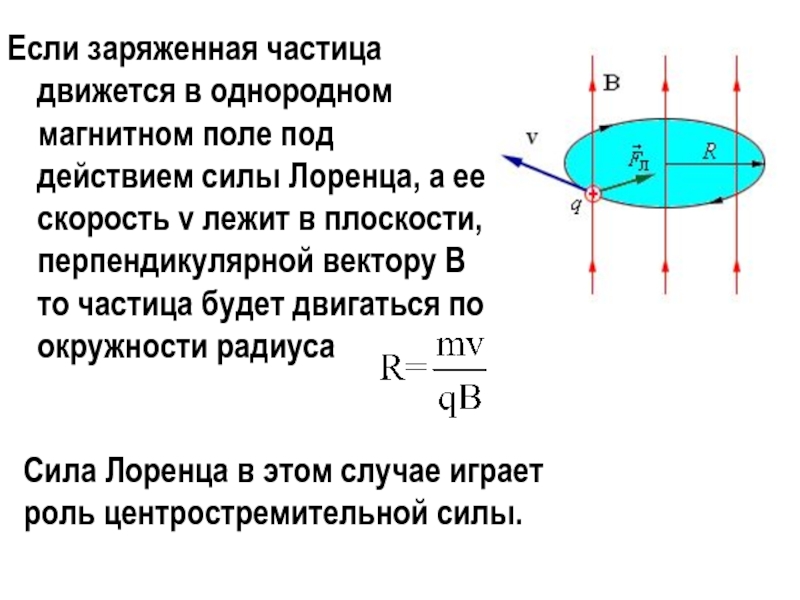
поле действует на движущейся электрический заряд с силой 
Слайд 19Если заряженная частица движется в однородном магнитном поле под действием
силы Лоренца, а ее скорость v лежит в плоскости, перпендикулярной
вектору B то частица будет двигаться по окружности радиусаСила Лоренца в этом случае играет роль центростремительной силы.
Слайд 20Период обращения частицы в однородном магнитном поле равен
Это выражение
показывает, что для заряженных частиц заданной массы m период обращения
не зависит от скорости v и радиуса траектории R. Угловая скорость движения заряженной частицы по круговой траектории:Называется циклотронной частотой.
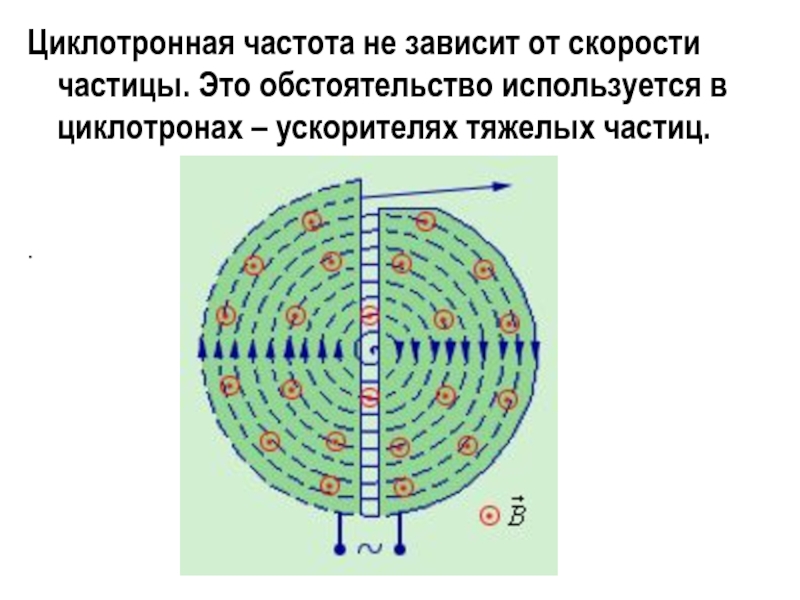
Слайд 21Циклотронная частота не зависит от скорости частицы. Это обстоятельство используется
в циклотронах – ускорителях тяжелых частиц.
.
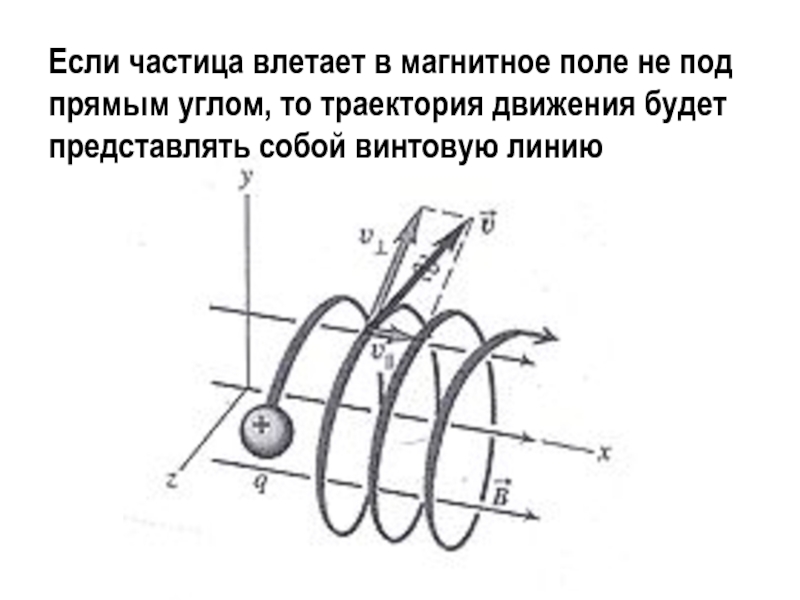
Слайд 22Если частица влетает в магнитное поле не под прямым углом,
то траектория движения будет представлять собой винтовую линию
Слайд 23 Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное
поле возникает в пространстве, окружающем проводники с током, подобно тому,
как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера)..
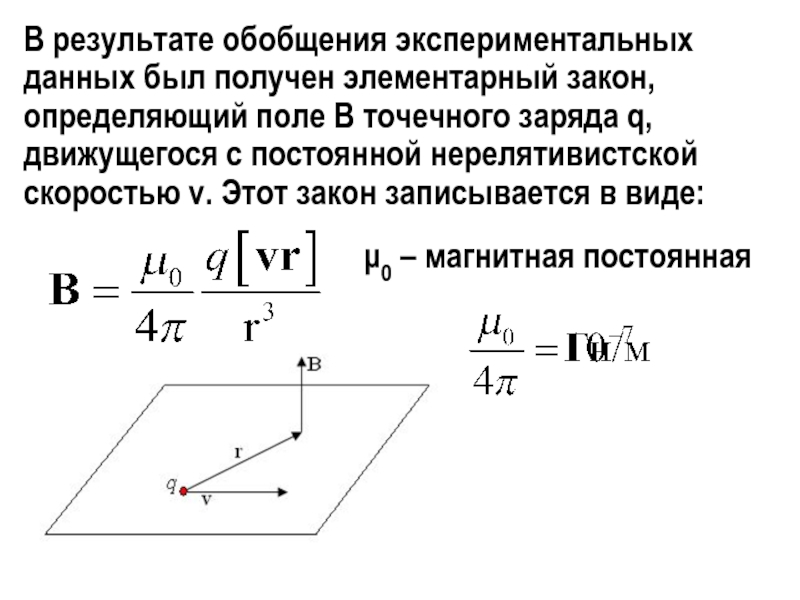
Слайд 24В результате обобщения экспериментальных данных был получен элементарный закон, определяющий
поле В точечного заряда q, движущегося с постоянной нерелятивистской скоростью
v. Этот закон записывается в виде:μ0 – магнитная постоянная
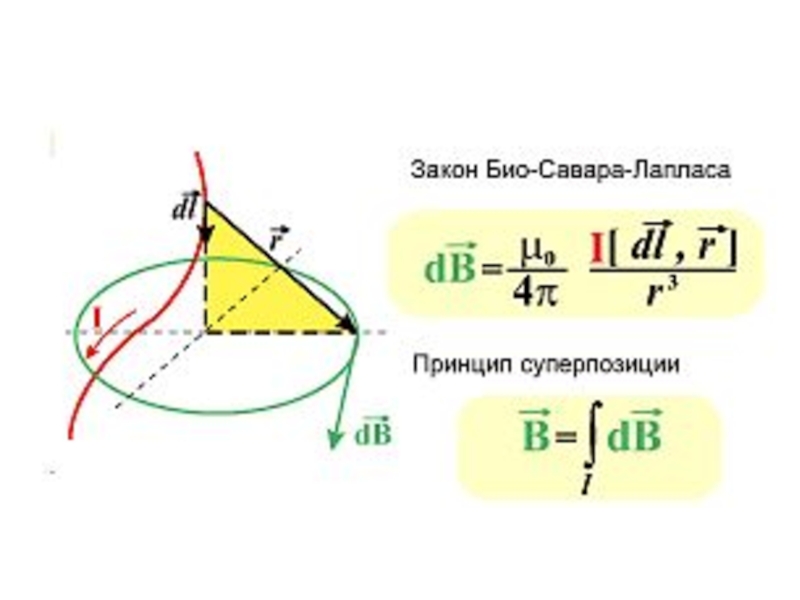
Слайд 25 Магнитное поле постоянных токов различной конфигурации изучалось
экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они
пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности.
Слайд 26Закон Био-Савара-Лапласа
Элементарный заряд q равен ρdV, где dV
– элементарный объем, ρ – объемная плотность заряда, являющегося носителем
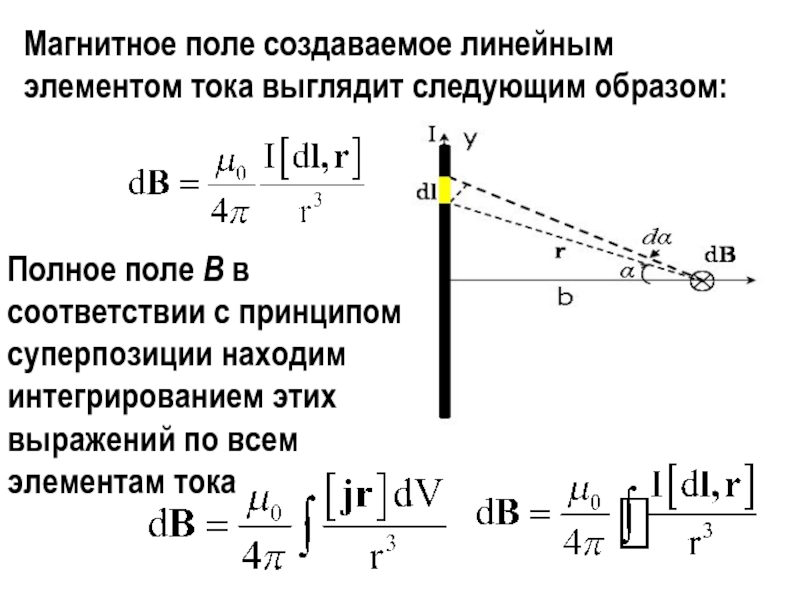
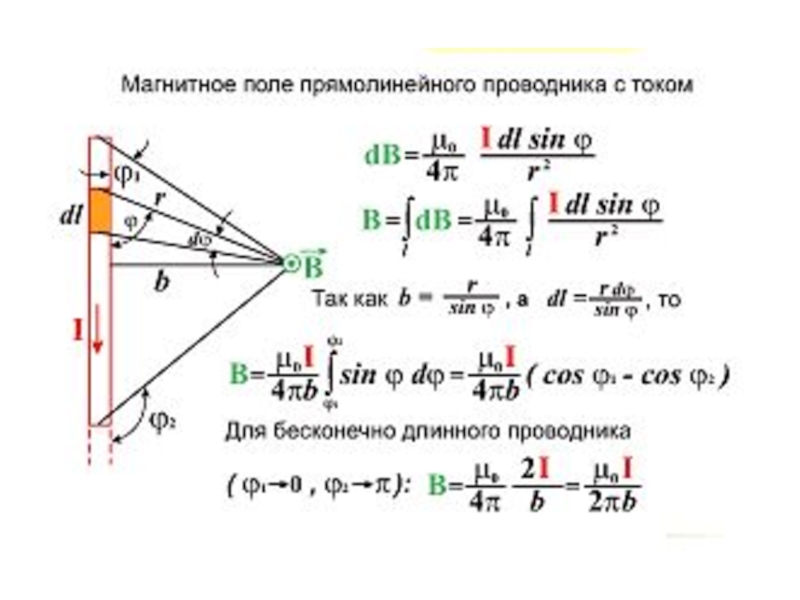
тока, учтем также, что ρv=j плотность тока. Тогда магнитное поле, создаваемое таким зарядом равно:
Слайд 27Магнитное поле создаваемое линейным элементом тока выглядит следующим образом:
Полное
поле В в соответствии с принципом суперпозиции находим интегрированием этих
выражений по всем элементам тока
Слайд 30 Как и любое другое векторное поле, поле В
может быть представлено наглядно с помощью силовых линий вектора В.
Их проводят так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора В, а густота линий была бы пропорциональна модулю вектора В в данном месте.
Слайд 31Магнитное поле обладает, как и электрическое поле, двумя важнейшими свойствами
– поток и циркуляция вектора В. Поток вектора В сквозь
любую замкнутую поверхность равен нулю:Равенство потока вектора В нулю также является следствием того, что в природе не существует магнитных зарядов на которых начинались бы или заканчивались линии магнитной индукции В.
Слайд 32 Расчеты магнитного поля токов можно выполнять с
помощью теоремы о циркуляции вектора магнитной индукции.
Выберем некоторый условный замкнутый
контур (не обязательно плоский) и укажем положительное направление обхода контура. 
Слайд 33 Теорема о циркуляция вектора В: циркуляция вектора
В по произвольному контуру равна произведению μ0 на алгебраическую сумму
токов, охватываемых контуром:
Слайд 34Причем Ik – величины алгебраические. Ток считается положительным, если его
направление связано с направлением обхода по контуру правилом правого винта.
Ток противоположного направления считается отрицательным.
Слайд 35Контрольные вопросы
Закон Джоуля-Ленца в интегральной и дифференциальной форме
Мощность тока
Законы Кирхгофа
Сила
Лоренца
Поток и циркуляция вектора магнитной индукции.
