Слайд 1Занятие 22
МДК.01.02 Программное обеспечение компьютерных сетей
3-курс
Слайд 2 Элементы теории массового обслуживания
Слайд 3Элементы теории массового обслуживания
1. Классификация систем массового обслуживания.
В каждую систему
массового обслуживания (СМО) поступает входящий поток заявок на обслуживание.
Результатом
работы системы массового обслуживания (СМО) является выходящий поток обслуженных заявок.
• Потоком событий называется последовательность однородных событий, происходящих в какие-то, вообще говоря, случайные моменты времени.
• Если в системе массового обслуживания (СМО) одновременно может обслуживаться несколько заявок, то СМО называется многоканальной, в противном случае СМО называется одноканальной.
Слайд 4Элементы теории массового обслуживания
• Как одноканальные СМО, так
и многоканальные СМО делятся на СМО с отказами и СМО
с очередью (ожиданием).
• В СМО с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, получает «отказ» в обслуживании и покидает СМО.
• В СМО с очередью заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь из заявок, ожидающих обслуживания. Как только один из каналов обслуживания освобождается, к обслуживанию принимается одна из заявок, стоящих в очереди.
• СМО с очередью различаются по принципу построения (дисциплине) очереди.
Слайд 5Элементы теории массового обслуживания
• Принципом построения очереди называется
схема, в соответствии с которой заявки из очереди выбираются на
обслуживание.
Чаще всего при этом используется:
1. Случайный выбор заявки из очереди;
2. Выбор заявки из очереди в зависимости от её приоритета;
3. Выбор заявки в зависимости от порядка её поступления в очередь.
В третьем случае заявки из очереди могут обслуживаться, как по схеме: «Первым пришел − первым обслуживаешься», так и по схеме: «Последним пришел − первым обслуживаешься».
Слайд 6Элементы теории массового обслуживания
• СМО с очередью делятся
также на СМО с неограниченным ожиданием и СМО с ограниченным
ожиданием.
• В СМО с неограниченным ожиданием каждая заявка, поступившая в СМО, рано или поздно будет обслужена.
• В СМО с ограниченным ожиданием на пребывание заявок в очереди накладываются различного рода ограничения.
Эти ограничения могут касаться, например, длины очереди, времени пребывания заявки в очереди, общего времени пребывания заявки в СМО и т.п.
В частности, в СМО с ограниченным временем пребывания в очереди, заявка, израсходовавшая лимит времени пребывания в очереди, покидает СМО.
Слайд 7Элементы теории массового обслуживания
2. Простейший поток событий и его свойства.
Поток
событий называется простейшим потоком событий, если он обладает следующими свойствами
стационарности, отсутствия последействия и ординарности:
1. Поток событий называется стационарным, если вероятность появления одного или нескольких событий на участке времени длины T зависит только от длины T этого участка и не зависит от того, в каком месте оси времени этот участок располагается.
2. Поток событий называется потоком с отсутствием последействия (без последействия), если события, составляющие поток, появляются в случайные моменты времени независимо друг от друга.
Слайд 8Элементы теории массового обслуживания
3. Поток событий называется ординарным,
если события, составляющие поток, происходят поодиночке, а не парами, тройками
и т.д.
Замечание. Поток, в котором события происходят через равные промежутки времени, не является простейшим потоком событий!
• Интенсивностью (плотностью) потока событий называется среднее число событий, происходящих в единицу времени.
Замечание. Простейший поток событий обладает постоянной интенсивностью. (В дальнейшем изложении будем предполагать, что все потоки событий являются простейшими потоками, не оговаривая этого особо.)
Слайд 9Элементы теории массового обслуживания
Простейший поток событий близко связан с распределением
Пуассона.
Действительно, справедливо следующее:
Утверждение 1. Вероятность того, что на отрезке
времени длины T произойдет ровно k событий из простейшего потока с интенсивностью λ, выражается формулой Пуассона:
Слайд 10Элементы теории массового обслуживания
Утверждение 2. Длина отрезка времени между последовательными
событиями из простейшего потока событий с интенсивностью λ является случайной
величиной, распределенной по показательному (экспоненциальному) закону с параметром λ.
Замечание. Напомним, что плотность показательного распределения определяется по формуле:
Слайд 11Элементы теории массового обслуживания
3. Показатели эффективности СМО.
Рассмотрим сначала СМО с
отказами.
Важнейшими показателями эффективности СМО с отказами являются следующие параметры:
1. Абсолютная пропускная способность системы;
2. Относительная пропускная способность системы.
• Абсолютной пропускной способностью СМО называется среднее число заявок, которое может обслужить система за единицу времени.
Слайд 12Элементы теории массового обслуживания
• Относительной пропускной способностью СМО
называется средняя доля поступивших заявок, обслуживаемая системой, т.е. отношение среднего
числа заявок, которое может обслужить система за единицу времени, к среднему числу заявок, поступивших в систему за это время.
В некоторых практических задачах используются и другие показатели эффективности СМО с отказами, например:
- среднее число занятых каналов,
- среднее относительное время простоя системы,
- среднее относительное время простоя отдельного канала и т.п.
Слайд 13Элементы теории массового обслуживания
Теперь рассмотрим СМО с ожиданием.
В качестве показателей
эффективности СМО с неограниченным ожиданием применяются следующие параметры:
1.
Среднее число заявок в очереди;
2. Среднее число обслуживаемых заявок;
3. Среднее время ожидания заявки в очереди;
4. Среднее время обслуживания заявки.
Поскольку в СМО с неограниченным ожиданием каждая заявка, в конце концов, обслуживается, то для таких систем абсолютная пропускная способность совпадает с интенсивностью входящего потока заявок.
Слайд 14Элементы теории массового обслуживания
У систем массового обслуживания (СМО) с ограниченным
ожиданием в качестве показателей эффективности используются:
- как
показатели эффективности СМО с отказами,
- так и показатели эффективности СМО с неограниченным ожиданием.
При исследовании многоканальных систем в дополнение к перечисленным выше показателям эффективности используются параметры, описывающие каждый из каналов.
Слайд 15Элементы теории массового обслуживания
4. Расчет показателей эффективности одноканальной СМО с
отказами.
Список используемых терминов и обозначений
Слайд 16Элементы теории массового обслуживания
Постановка задачи. Параметры λ и μ известны.
Требуется
найти
Формулы для расчетов. В теории массового обслуживания доказывается, что показатели
эффективности одноканальной СМО с отказами вычисляются по следующим формулам:
Слайд 17Элементы теории массового обслуживания
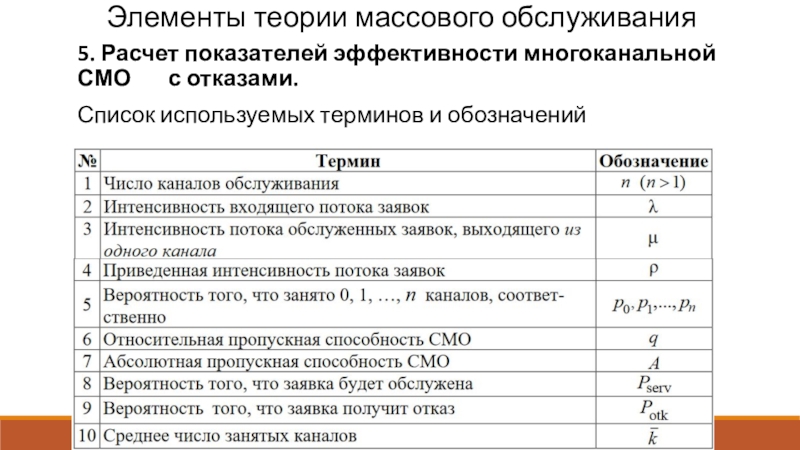
5. Расчет показателей эффективности многоканальной СМО
с отказами.
Список используемых терминов и обозначений
Слайд 18Элементы теории массового обслуживания
Постановка задачи. Параметры λ и μ известны.
Требуется
найти
Формулы для расчетов. Приведенная интенсивность потока заявок вычисляется по формуле:
Вероятности
вычисляются по формулам Эрланга:
Слайд 19Элементы теории массового обслуживания
Поскольку заявка получает отказ, если все каналы
обслуживания заняты, то
Кроме того,
Слайд 20Элементы теории массового обслуживания
6. Расчет
показателей
эффективности
одноканальной
СМО
с
ограниченной
очередью.
Список
используемых
терминов
и обозначений
Слайд 21Элементы теории массового обслуживания
Постановка задачи. Параметры λ и μ известны.
Требуется
найти
Формулы для расчетов. Приведенная интенсивность потока заявок вычисляется по формуле:
Вероятности
вычисляются по следующим формулам:
Слайд 22Элементы теории массового обслуживания
Поскольку заявка получает отказ, если СМО занята,
а в очереди находятся m заявок, то
далее получаем
Слайд 23Элементы теории массового обслуживания
Кроме того, справедливы формулы
Слайд 24Элементы теории массового обслуживания
6. Расчет
показателей
эффективности
одноканальной
СМО
с
неограниченной
очередью.
Список
используемых
терминов
и обозначений
Слайд 25Элементы теории массового обслуживания
Постановка задачи. Параметры λ и μ известны.
Требуется
найти
Формулы для расчетов. Приведенная интенсивность потока заявок вычисляется по формуле:
Если
в формулах из предыдущего раздела (№ 6) перейти к пределу при , то мы получим следующие формулы:
Слайд 26Элементы теории массового обслуживания
В случае очереди бесконечной длины каждая заявка,
в конце концов, будет обслужена. Следовательно,
Кроме того, справедливы формулы
Слайд 27Элементы теории массового обслуживания
8. Примеры.
Пример 1.
На вход многоканальной СМО с
отказами поступает поток заявок, интенсивность которого составляет 11 заявок/час.
Среднее
время обслуживания одной заявки 0,15 часа.
Каждая заявка приносит доход 130 руб., а содержание одного канала обходится в 122 руб./час.
Найти оптимальное число каналов СМО.
Слайд 28Элементы теории массового обслуживания
Решение.
Воспользовавшись данными из условия задачи и
обозначениями, принятыми в пункте 5, проведем следующие вычисления:
Слайд 29Элементы теории массового обслуживания
Из условия задачи также вытекает, что в
случае, если СМО имеет n каналов, то она приносит доход
D=D(n), который можно определить по формуле
где A=A(n) − абсолютная пропускная способность СМО.
В случае, когда число каналов n=1, из формул раздела №5 получаем
Слайд 30Элементы теории массового обслуживания
При n=2
Слайд 31Элементы теории массового обслуживания
При n=3
Слайд 32Элементы теории массового обслуживания
При n=4
Слайд 33Элементы теории массового обслуживания
При n=5
Слайд 34Элементы теории массового обслуживания
Сравнивая доходы, поступающие от СМО в случаях
n=1,2,3,4,5, замечаем, что при увеличении числа каналов от одного до
четырех доход растет и при n=4 становится наибольшим.
Это значение и является оптимальным.
Ответ.
Оптимальным является наличие в СМО 4-х каналов.
Слайд 35Элементы теории массового обслуживания
Пример 2.
К пункту мойки автомашин, рассчитанному на
одну автомашину, подъезжает в среднем 5 машин в час.
Процесс мойки
одной автомашины занимает в среднем 15 минут.
Рядом с пунктом мойки расположена площадка для ожидающих мойки автомашин, вмещающая 3 автомашины.
Если площадка занята, то приезжающие для мойки автомашины уезжают в другие пункты мойки.
Определить показатели эффективности этой системы массового обслуживания (СМО).
Слайд 36Элементы теории массового обслуживания
Решение.
Данная СМО является одноканальной СМО с очередью
на 3 заявки.
Интенсивность входящего потока заявок
λ=5 заявок/час.
Интенсивность выходящего потока обслуженных заявок
Воспользовавшись далее формулами из раздела №6, получим
Слайд 37Элементы теории массового обслуживания
Слайд 38Элементы теории массового обслуживания
Этот расчет и завершает решение задачи.
Среднее время
ожидания заявки в очереди – 0,31 часа,
Среднее время пребывания заявки
в системе массового обслуживания – 0,49 часа.
Слайд 39Список литературы:
1. Вентцель Е.С. Исследование операций: Задачи, принципы, методология. Учебное
пособие -М.: Дрофа, 2004.
2. Гнеденко Б.В., КоваленкоИ.Н. Введение в теорию
массового обслужи-вания. –М.: КомКнига, 2005.
3. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика: Учебник. –М.: ИНФРА-М, 2002.
4. Оуэн Г. Теория игр. –М.: Вузовская книга, 2004.
Слайд 40Благодарю за внимание!
Преподаватель: Солодухин Андрей Геннадьевич
Электронная почта: asoloduhin@kait20.ru