Жадные алгоритмы

Элементы жадной стратегии
Жадный

алгоритм позволяет получить оптимальное решение задачи путем осуществления ряда выборов. В каждой точке принятия решения в алгоритме де­лается выбор, который в данный момент выглядит самым лучшим. Эта эвристи­ческая стратегия не всегда дает оптимальное решение, но все же решение может оказаться и оптимальным.
Процесс разработки жадных алгоритмов можно представить в виде последовательности перечисленных ниже этапов.
1. Привести задачу оптимизации к виду, когда после сделанного выбора оста­ется решить только одну подзадачу.
2. Доказать, что всегда существует такое оптимальное решение исходной за­дачи, которое можно получить путем жадного выбора, так что такой выбор всегда допустим.
3. Показать, что после жадного выбора остается подзадача, обладающая тем свойством, что объединение оптимального решения подзадачи со сделанным жадным выбором приводит к оптимальному решению исходной задачи.
Описанный выше процесс будет использоваться в последующих задачах.
Замечание. В основе каждого жадного алгоритма почти всегда находится более сложное решение в стиле динамического программирования.
Вопрос. Как определить, способен ли жадный алгоритм решить стоящую перед нами задачу оптимизации? Общего пути здесь нет, однако можно выделить две ос­новные составляющие – свойство жадного выбора и оптимальную подструктуру. Если удается продемонстрировать, что задача обладает двумя этими свойствами, то с большой вероятностью для нее можно разработать жадный алгоритм.

Свойство жадного

выбора
Первый из названных выше основных составляющих жадного алгоритма – свойство жадного выбора: глобальное оптимальное решение можно получить, делая локальный оптимальный (жадный) выбор. Другими словами, рассуждая по поводу того, какой выбор следует сделать, мы делаем выбор, который кажется самым лучшим в текущей задаче; результаты возникающих подзадач при этом не рассматриваются.
Рассмотрим отличие жадных алгоритмов от динамического программирова­ния.
В динамическом программировании на каждом этапе делается выбор, од­нако обычно этот выбор зависит от решений подзадач. Следовательно, методом динамического программирования задачи обычно решаются в восходящем на­правлении, т.е. сначала обрабатываются более простые подзадачи, а затем – бо­лее сложные.
В жадном алгоритме делается выбор, который выглядит в данный момент наилучшим, после чего решается подзадача, возникающая в результате этого выбора. Выбор, сделанный в жадном алгоритме, может зависеть от сделан­ных ранее выборов, но он не может зависеть от каких бы то ни было выборов или решений последующих подзадач. Таким образом, в отличие от динамическо­го программирования, где подзадачи решаются в восходящем порядке, жадная стратегия обычно разворачивается в нисходящем порядке, когда жадный выбор делается один за другим, в результате чего каждый экземпляр текущей задачи сводится к более простому.

Оптимальная подструктура

Оптимальная подструктура проявляется в задаче, если в ее оптимальном ре­шении содержатся оптимальные решения подзадач. Это свойство является основ­ным признаком применимости как динамического программирования, так и жад­ных алгоритмов. В качестве примера оптимальной подструктуры рассмотрим следующую задачу.
Задача о выборе процессов
Составить расписание для нескольких конкурирующих процессов, каждый из которых безраздельно исполь­зует общий ресурс. Цель этой задачи – выбор набора взаимно совместимых про­цессов, образующих множество максимального размера. Предположим, имеется множество S = {a1, a2,..., an}, состоящее из п процессов.
Процессам требуется некоторый ресурс, который одновременно может использоваться лишь одним процессом. Каждый процесс ai характеризуется начальным моментом si и конечным моментом fi, где 0 ≤ si < fi < . Будучи выбран, процесс аi длит­ся в течение полуоткрытого интервала времени [si , fi). Процессы ai и aj совме­стимы, если интервалы [si , fi) и [sj , fj) не перекрываются (т.е. если si ≥fj или sj ≥ fi). Задача о выборе процессов заклю­чается в том, чтобы выбрать подмножество взаимно совместимых процессов, об­разующих множество максимального размера. Например, рассмотрим описанное ниже множество S процессов, отсортированных в порядке возрастания моментов окончания:
i
si
fi

на несколько этапов. Начнем с того, что сформулируем решение рассматриваемой

задачи, основанное на принципах динамического программирования. Это оптимальное решение исходной задачи получается путем комбинирования оптимальных решений подзадач. Рассмотрим несколько вариантов выбора, который делается в процессе определения подзадачи, исполь­зующейся в оптимальном решении. Впоследствии станет понятно, что заслуживает внимания лишь один выбор – жадный — и что когда делается этот выбор, одна из подзадач гарантированно получается пустой. Остается лишь одна непу­стая подзадача. Исходя из этих наблюдений, мы разработаем рекурсивный жадный алгоритм, предназначенный для решения задачи о составлении расписания про­цессов. Процесс разработки жадного алгоритма будет завершен его преобразова­нием из рекурсивного в итерационный. Описанные в этом разделе этапы сложнее, чем те, что обычно имеют место при разработке жадных алгоритмов, однако они иллюстрируют взаимоотношение между жадными алгоритмами и динамическим программированием.

задачи о выборе процессов
Разработаем

вначале решение для задачи о выборе процессов по методу динамического программирования. Первый шаг будет состоять в том, чтобы найти оптимальную подструктуру и с ее помощью построить оптимальное решение задачи, пользуясь оптимальными решениями подзадач.
Для этого нужно определить подходящее про­странство подзадач. Начнем с определения множеств Sij = {аk ∊ S : fi≤sk < fk ≤ sj}.
Sij – подмножество процессов из множества S, которые можно успеть выполнить в промежутке времени между завершением процесса аi и началом процесса аj. Фактически множество Sij состоит из всех процессов, совместимых с процессами аi и аj.а также теми, которые оканчиваются не позже процесса аi и теми, кото­рые начинаются не ранее процесса аj. Для представления всей задачи добавим фиктивные процессы а0 и аn+1 и примем соглашение, что f0 = 0 и sn+1 = . Тогда S = S0,n+1, а индексы i и j находятся в диапазоне 0 ≤ i,j≤ п + 1.
Предположим далее, что процессы отсортиро­ваны в порядке возрастания соответствующих им конечных моментов времени:
f0 ≤ f1 ≤ . . . ≤fn≤fn+1. (1)
Очевидно, что в этом случае Sij =  = {}, если i≥j. Предположим, что это не так, т.е. существует процесс ak∊Sij для некоторого i≥j, так что процесс аi следует после процесса aj, если расположить их в порядке сортировки, Однако из определения Sij следует соотношение fi ≤ sk< fk ≤sj ≤fj, откуда fi 0≤i

процессов, рассмотрим некото­рую непустую подзадачу Sij1 и предположим, что ее

решение включает некоторый процесс ak, так что fi ≤ sk< fk ≤sj. С помощью процесса ak генерируются две подзадачи, Sik (процессы, которые начинаются после окончания процесса ai и заканчиваются перед началом процесса аk) и Skj (процессы, которые начина­ются после окончания процесса ak и заканчиваются перед началом процесса аj), каждая из которых состоит из подмножества процессов, входящих в Sij. Решение задачи представляет собой объединение решений задач Sik , Skj и процесса аk. Таким образом, количество процессов, входящее в состав решения задачи – это сумма количества процессов в решении задачи Sik, количества процессов в решении задачи Skj и еще одного процесса (аk).
Опишем оптимальную подструктуру этой задачи. Предположим, что опти­мальное решение Aij задачи Sij включает в себя процесс аk,. Тогда решения Aik задачи Sik и Akj задачи Skj в рамках оптимального решения Sij тоже должны быть оптимальными. Как обычно, это доказывается с помощью рассуждений типа "вырезания и вставки". Если бы существовало решение A'iik задачи Sik, включа­ющее в себя большее количество процессов, чем Aik , в решение Aij можно было бы вместо Aik подставить A'iik, что привело бы к решению задачи Sij, в котором содержится больше процессов, чем в Aij. Поскольку предполагается, что Aij – оптимальное решение, мы приходим к противоречию. Аналогично, если бы су­ществовало решение А'kjзадачи Skj, содержащее больше процессов, чем Akj, то путем замены Akj на А'kj, можно было бы получить решение задачи Sij, в которое входит больше процессов, чем в Aij.

подструктуры пока­жем, что оптимальное решение задачи можно составить из оптимальных

решений подзадач. Мы уже знаем, что в любое решение непустой задачи Sij входит неко­торый процесс аk, и что любое оптимальное решение задачи содержит в себе оптимальные решения подзадач Sik и Skj. Таким образом, максимальное подмно­жество взаимно совместимых процессов множества Sij можно составить путем разбиения задачи на две подзадачи (определение подмножеств максимального раз­мера, состоящих из взаимно совместимых процессов в задачах Sik и Skj – соб­ственно нахождения максимальных подмножеств Aik и Akj заимно совместимых процессов, являющихся решениями этих подзадач, и составления подмножества Aij максимального размера, включающего в себя взаимно совместимые задачи:
Aij = AikU{ak}UAkj. (2)
Оптимальное решение всей задачи представляет собой решение задачи S0,n+I .

Рекурсивное решение

Второй этап разработки решения по методу динамического программирова­ния – определение значения, соответствующего оптимальному решению. Пусть в задаче о выборе процесса c[i,j] – количество процессов в подмножестве мак­симального размера, состоящем из взаимно совместимых процессов в задаче Sij. Эта величина равна нулю при Sij = ; в частности, с [i j] = 0 при i ≥ j.
Теперь рассмотрим непустое подмножество Sij. Мы уже знаем, что если про­цесс аk используется в максимальном подмножестве, состоящем из взаимно сов­местимых процессов задачи Sij, то для подзадач Sik и Skj также используются подмножества максимального размера. С помощью уравнения (2) получаем рекуррентное соотношение
c[i,j] = с[i,k] + c[k,j] + 1.
В приведенном выше рекурсивном уравнении предполагается, что значение k известно, но на самом деле это не так. Это значение можно выбрать из j - i - 1 возможных значений: k = i +1, . . . j- 1. Поскольку в подмножестве максимального
размера для задачи Sij должно использоваться одно из этих значений k, нужно проверить, какое из них подходит лучше других. Таким образом, полное
рекурсивное определение величины c[i,j] принимает вид:
c[i,j] = 0 при Sij = ;
c[i,j] = max { с[i,k] + c[k,j] + 1 | i

данном этапе не составляет труда написать восходящий алгоритм динами­ческого программирования,

основанный на рекуррентном уравнении (3). Это предлагается сделать читателю в упражнении. Однако можно сделать два наблюдения, позволяющие упростить полученное решение.
Теорема. Рассмотрим произвольную непустую задачу Sij и пусть ат – про­цесс, который оканчивается раньше других:
fm = max{fk: ak∊ Sij}.
В этом случае справедливы такие утверждения.
1. Процесс ат используется в некотором подмножестве максимального разме­ра, состоящем из взаимно совместимых процессов задачи Sij.
2. Подзадача Sim пустая, поэтому в результате выбора процесса аm непустой остается только подзадача Smj.

совместимых процессов задачи Sij, и упорядочим про­цессы этого подмножества в

порядке возрастания времени их окончания. Пусть ak — первый процесс множества Aij. Если ak = аm, то доказательство завершено, поскольку мы показали, что процесс ат используется в некотором подмножестве максимального размера, состоящем из взаимно совместимых процессов задачи Sij. Если же ak ≠ аm, то составим подмножество A'ij = Aij - {ak}U{аm}. Процессы в A'ij не перекрываются, поскольку процессы во множестве Aij не перекрываются, ak –процесс из множества Aij, который оканчивается раньше всех, и fm ≤ fk . Заметим, что количество процессов во множестве A'ij совпадает с количеством процессов во множестве Aij, поэтому A'ij – подмножество мак­симального размера, состоящее из взаимно совместимых процессов задачи Sij, и включающее в себя процесс аm.
п.2. Предположим, что подзадача Sim непустая и существует некоторый процесс ak такой что fi ≤ sk < fk ≤ sm < fm. Тогда процесс также входит в решение подзадачи Sim, причем он оканчивается раньше, чем процесс аm, что противоречит выбору процесса аm. Таким образом, мы приходим к выводу, что решение подзадачи Sim – пустое множество.

т

первого процесса в Si,n+1}
do т ⟵ т + 1
if т ≤ n
then return { аm } U Recursive_Activity_Selector (s , f, m, n)
else return 

п
do if sm ≥ fi

then A ⟵ A u {am}
i ⟵ m
8 return A

Упражнения
1. Разработайте алгоритм динамического программирования для решения задачи о выборе процессов, основанный на рекуррентном соотношении (3). В этом алгоритме должны вычисляться определенные выше разме­ры с[i,j], а также выводиться подмножество процессов А максимального размера. Предполагается, что процессы отсортированы в порядке, задан­ном уравнением (1). Сравните время работы найденного алгоритма со временем работы процедуры Greedy_Activity_Selector.
2. Предположим, что вместо того, чтобы все время выбирать процесс, кото­рый оканчивается раньше других, выбирается процесс, который начина­ется позже других и совместим со всеми ранее выбранными процессами. Опишите этот подход как жадный алгоритм и докажите, что он позволяет получить оптимальное решение.
3. Предположим, что имеется множество процессов, для которых нужно со­ставить расписание при наличии большого количества ресурсов. Цель – включить в расписание все процессы, использовав при этом как мож­но меньше ресурсов. Сформулируйте эффективный жадный алгоритм, позволяющий определить, какой ресурс должен использоваться тем или иным процессом.
(Эта задача известна также как задача о раскрашивании интервального графа (interval-graph colouring problem). Можно создать интервальный граф, вершины которого сопоставляются заданным процессам, а ребра соединяют несовместимые процессы. Минимальное количество цветов, необходимых для раскрашивания всех вершин таким образом, чтобы ни­какие две соединенные вершины не имели один и тот же цвет, будет рав­но минимальному количеству ресурсов, необходимых для работы всех заданных процессов.)
4. Не все жадные подходы к задаче о выборе процессов позволяют полу­чить множество, состоящее из максимального количества взаимно сов­местимых процессов. Приведите пример, иллюстрирующий, что выбор самых коротких процессов среди тех, что совместимы с ранее выбран­ными, не дает правильного результата. Выполните такое же задание для подходов, в одном из которых всегда выбирается процесс, совместимый с ранее выбранными и перекрывающийся с минимальным количеством оставшихся, а в другом — совместимый с ранее выбранными процесс, который начинается раньше других.

и динамического программирования

Дискретная задача о рюкзаке

формулируется сле­дующим образом. Вор во время ограбления магазина обнаружил n предметов. Предмет под номером i имеет стоимость vi грн. и вес wi кг, где и vi и wi – целые числа. Нужно унести вещи, суммарная стоимость которых была бы как можно большей, однако грузоподъемность рюкзака ограничивается W килограммами, где W – целая величина. Какие предметы следует взять с собой?
Ситуация в непрерывной задаче о рюкзаке (fractional knapsack problem) та же, но теперь тот или иной товар вор может брать с собой частично, а не делать каждый раз бинарный выбор – брать или не брать (0-1). В дискретной задаче о рюкзаке в роли предметов могут выступать, например, слитки золота, а для непрерывной задачи больше подходят такие товары, как золотой песок.

Упражнения
1. Докажите, что непрерывная задача о рюкзаке обладает свойством жад­ного выбора.
2. Приведите решение дискретной задачи о рюкзаке с помощью динамиче­ского программирования. Время работы вашего алгоритма должно быть равно О (nW), где п — количество элементов, a W – максимальный вес предметов, которые вор может положить в свой рюкзак.
3. Предположим, что в дискретной задаче о рюкзаке порядок сортировки по увеличению веса совпадает с порядком сортировки по уменьшению стои­мости. Сформулируйте эффективный алгоритм для поиска оптимального решения этой разновидности задачи о рюкзаке и обоснуйте его коррект­ность.
4. Путешественник едет из Киева в Москву на автомобиле. У него есть карта, где обозначены все заправки с указанием расстояния между ними. Извест­но, что если топливный бак заполнен, то автомобиль может проехать n километров. Путешественнику хочется как можно реже останавливаться на за­правках. Сформулируйте эффективный метод, позволяющий путешественнику определить, на каких заправках следует заливать топливо, чтобы коли­чество остановок оказалось минимальным. Докажите, что разработанная стратегия дает оптимальное решение.
6. Покажите, как решить непрерывную задачу о рюкзаке за время О (n).

Коды Хаффмана
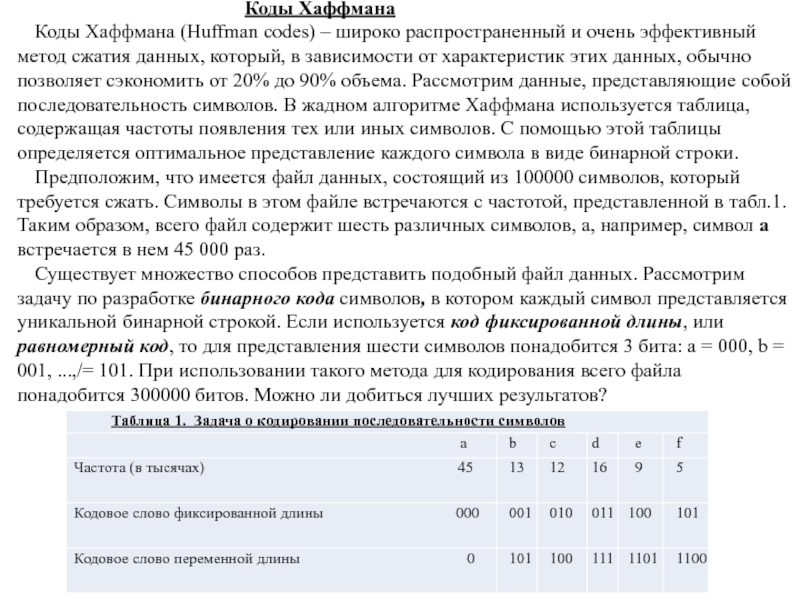
Коды Хаффмана (Huffman codes) – широко распространенный и очень эф­фективный метод сжатия данных, который, в зависимости от характеристик этих данных, обычно позволяет сэкономить от 20% до 90% объема. Рассмотрим данные, представляющие собой последовательность символов. В жадном алго­ритме Хаффмана используется таблица, содержащая частоты появления тех или иных символов. С помощью этой таблицы определяется оптимальное представ­ление каждого символа в виде бинарной строки.
Предположим, что имеется файл данных, состоящий из 100000 символов, который требуется сжать. Символы в этом файле встречаются с частотой, пред­ставленной в табл.1. Таким образом, всего файл содержит шесть различных символов, а, например, символ а встречается в нем 45 000 раз.
Существует множество способов представить подобный файл данных. Рас­смотрим задачу по разработке бинарного кода символов, в котором каждый символ представляется уни­кальной бинарной строкой. Если используется код фиксированной длины, или равномерный код, то для представления шести символов пона­добится 3 бита: а = 000, b = 001, ...,/= 101. При использовании такого метода для кодирования всего файла понадобится 300000 битов. Можно ли добиться лучших результатов?

или неравномерного кода, удается получить значительно лучшие результаты, чем с

помощью кода фиксированной длины. Это достигается за счет того, что часто встречающим­ся символам сопоставляются короткие кодовые слова, а редко встречающимся – длинные. Такой код представлен в последней строке табл.1. В нем символ а представлен 1-битовой строкой 0, а символ f — 4-битовой строкой 1100. Для представления файла с помощью этого кода потребуется
(45 • 1 + 13 • 3 + 12 • 3 + 16 • 3 + 9 • 4 + 5 • 4) • 1000 = 224000 битов.
Благодаря этому дополнительно экономится 25% объема.
Для рассматриваемого файла это оптимальная кодировка символов.

1 to n – 1
do Выделить память

для узла z
left [z] ⟵ х ⟵ Extract_Min(Q)
right [z] ⟵ у ⟵ Extract_Min(Q)
f [z] ⟵ f [x] + / f [y]
Insert(Q, z)
return Extract_Min(Q) //Возврат корня дерева

Очереди с приоритетами
Одно из наиболее популярных применений пирамид – создание и эффективная работа очередей с приоритетами. Как и пирамиды, очереди с приоритетами бывают двух видов: невозрастающие и неубывающие.
Очередь с приоритетами – это структура данных, предна­значенная для обслуживания множества S, с каждым элементом которого связано определенное значение, называющееся ключом (key). В невозрастающей (неубывающей) очере­ди с приоритетами поддерживаются следующие операции.
Операция Insert(S, х) вставляет элемент х в множество 5. Эту операцию можно записать как S⟵ S U {х}.
Операция Maximum(S) (Minimum(S) ) возвращает элемент множества S с наибольшим (наименьшим) ключом.
Операция Extract_Max(S) (Extract_Min(S)) возвращает элемент с наибольшим (наименьшим) ключом, удаляя его при этом из множества S.
Операция Increase_Key(S, х, k) (Decrease_Key(S, х, k)) увеличивает (уменьшает) значение ключа, соответству­ющего элементу х, путем его замены ключом со значением k. Предполага­ется, что величина k не меньше (не больше) текущего ключа элемента х.
В очередь в любое время можно добавить новое задание, воспользовавшись операцией Heap_Insert.
Приоритетную очередь можно реализовать с помощью пирамиды. Если очередь с приоритетами реализует­ся с помощью пирамиды, то в каждом элементе пирамиды приходится хранить идентификатор соответствующего объекта приложения. В каждом объекте приложения точно так же необходимо хранить идентификатор соответствующего элемента пирамиды, как правило, это будет индекс массива.