Начальные сведения из теории вероятностей 9 класс

Содержание

1. Начальные сведения из теории вероятностей 9 класс
2. Слайд 2
3. Вероятность случайного события
4. Всякий результат, полученный в процессе наблюдения
5. Закономерности случайных событий изучает специальный раздел математики, который называется - теорией вероятностей
6. Относительной частотой случайного события в серии
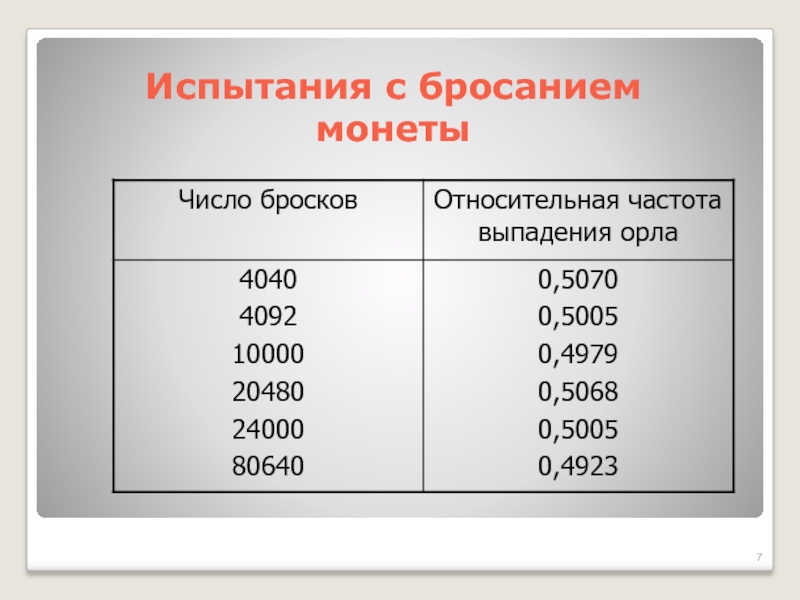
7. Испытания с бросанием монеты
8. Результаты наблюдений и опытов показывают, что
9. Вероятностью события называется отношение
10. Событие, которое никогда не может произойти, сколько
11. Событие, которое происходит всегда, сколько бы раз
12. В усадьбе пруд тоже замёрз, но отяжелевшая
13. 9.77 В саду было совершенно
14. 9.80Многократная проверка показала, что всхожесть семян огурцов
15. 9.82 Какова вероятность того, что при бросании
16. 9.85 Андрей и Витя договорились, что если
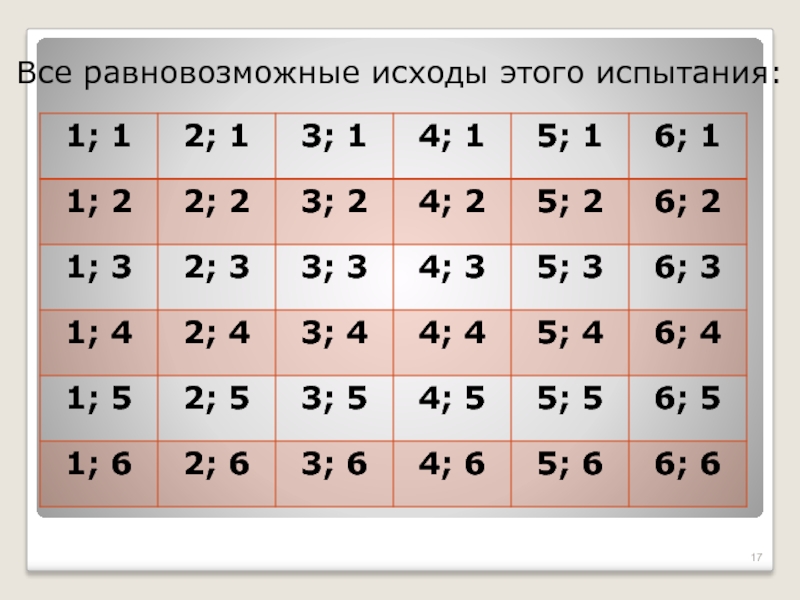
17. Все равновозможные исходы этого испытания:
18. Событие А означает, что при бросании
19. Урок окончен!
20. Скачать презентанцию

Вероятность случайного события

Главная
Алгебра
Начальные сведения из теории вероятностей 9 класс

Слайды и текст этой презентации

Слайд 1Начальные сведения из теории вероятностей
9 класс

Слайд 2

Слайд 3Вероятность случайного события

Слайд 4 Всякий результат, полученный в процессе наблюдения или эксперимента, будем

называть событием

Событие, которое может произойти, а может и не произойти,

называется случайным событием

Всякий результат, полученный в процессе наблюдения или эксперимента, будем называть событиемСобытие, которое может произойти, а может

Слайд 5 Закономерности случайных событий изучает специальный раздел математики, который называется

- теорией вероятностей

Слайд 6 Относительной частотой случайного события в серии испытаний называется отношение

числа испытаний, в которых это событие наступило, к числу всех

испытаний

Слайд 7Испытания с бросанием монеты

Слайд 8 Результаты наблюдений и опытов показывают, что при большом числе

испытаний, проводимых в одних и тех же условиях, относительная частота

принимает достаточно устойчивое значение и принимается за вероятность случайного события

Такое определения называют статистическим определением вероятности

Результаты наблюдений и опытов показывают, что при большом числе испытаний, проводимых в одних и тех же

Слайд 9 Вероятностью события называется отношение числа благоприятных для

него исходов испытания к числу всех равновозможных исходов.

Это классическое

определение вероятности.

Вероятностью события называется отношение числа благоприятных для него исходов испытания к числу всех равновозможных

Слайд 10Событие, которое никогда не может произойти, сколько бы раз ни

повторялось испытание, называется - невозможным событием.
Вероятность невозможного события равна 0.

Событие, которое никогда не может произойти, сколько бы раз ни повторялось испытание, называется - невозможным событием.Вероятность невозможного

Слайд 11Событие, которое происходит всегда, сколько бы раз ни повторялось испытание,

называется - достоверным событием.
Вероятность достоверного события равна 1

Событие, которое происходит всегда, сколько бы раз ни повторялось испытание, называется - достоверным событием.Вероятность достоверного события равна

Слайд 12
В усадьбе пруд тоже замёрз, но отяжелевшая и потемневшая речка

мельницы всё ещё сочилась в своих пушистых берегах и шумела

на шлюзах.
Пётр подошёл к плотине и остановился, прислушиваясь. Звон воды стал другим. Он стал тяжелее и потерял свою мелодию. В нём как будто чувствовался холод помертвевших окрестностей. В душе Петра тоже было холодно и сумрачно.
В настроении слепого юноши беспросветная грусть сменялась раздражительностью. Но вместе с тем возрастала замечательная тонкость его ощущений. Слух его чрезвычайно обострился. Свет он ощущал всем своим организмом и даже мог отличить лунные ночи от тёмных. (По В.Г.Короленко) (152 слова)

В усадьбе пруд тоже замёрз, но отяжелевшая и потемневшая речка мельницы всё ещё сочилась в своих пушистых

Слайд 13 9.77
В саду было совершенно тихо. Замёрзшая земля,

покрытая пушистым слоем снега, совершенно смолкла, не отдавая звуков. Зато

воздух стал как-то особенно чуток, отчётливо и полно перенося на далёкие расстояния крик вороны, удар топора, легкий треск обломавшейся ветки.
Найдем относительную частоту появления буквы о.
Всего букв - 217. Буква о – 29.

Относительная частота -

9.77 В саду было совершенно тихо. Замёрзшая земля, покрытая пушистым слоем снега, совершенно смолкла, не

Слайд 149.80
Многократная проверка показала, что всхожесть семян огурцов определенного сорта равна

0,9. Посадили 85 семян этого сорта. Найдите ожидаемое число проросших

семян.

Р = 0,9
n = 85
m = 0,9 * 85 = 76,5 ≈ 77 (семян)

9.80Многократная проверка показала, что всхожесть семян огурцов определенного сорта равна 0,9. Посадили 85 семян этого сорта. Найдите

Слайд 159.82
Какова вероятность того, что при бросании игрального кубика выпадет:
а)

одно очко; б) более 3 очков?

а) Р=

б) больше трех баллов,

т.е. 4, 5, 6. значит

Р =

9.82 Какова вероятность того, что при бросании игрального кубика выпадет:а) одно очко; б) более 3 очков?а) Р=б)

Слайд 169.85
Андрей и Витя договорились, что если при бросании двух

игральных кубиков в сумме выпадет число очков, кратное 5, то

выигрывает Андрей, а если в сумме выпадет число очков, кратное 6, то выигрывает Витя.
Справедлива ли эта игра и если нет,
то у кого из мальчиков
больше шансов выиграть?

9.85 Андрей и Витя договорились, что если при бросании двух игральных кубиков в сумме выпадет число очков,

Слайд 17Все равновозможные исходы этого испытания:

Слайд 18 Событие А означает, что при бросании кубика в сумме

выпало 5 или 10, а событие В означает, что в

сумме выпало 6 или 12.
Для А благоприятны 7 исходов
(1;4), (2;3), (3;2), (4,1), (4;6), (5;5), (6;4)
Для В благоприятны 6 исходов
(1;5), (2;4), (3;3), (4;2), (5;1), (6;6)
Отсюда:

Р(А)= Р(В) =