Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обобщение и систематизация знаний по теме Производная 10 класс
Содержание
- 1. Обобщение и систематизация знаний по теме Производная 10 класс
- 2. тип урока: обобщающий Цели
- 3. Слайд 3
- 4. Проверка домашнего задания 1. Сформулируйте определение производной функции в точке.2.Пользуясь определением производной, найдите f ‘(x),если:
- 5. 3. Поясните геометрический и механический смысл производной4.
- 6. 6.Перечислить формулы и правила дифференцирования:а) тригонометрических функций;б)степенной
- 7. Итак, мы обобщили основные
- 8. Слайд 8
- 9. Разбор подходов
- 10. Б)f '(x)
- 11. 3. Заданы функции f(x)=3-2x¸g(x)=x² и p(x)=sinx. Задайте
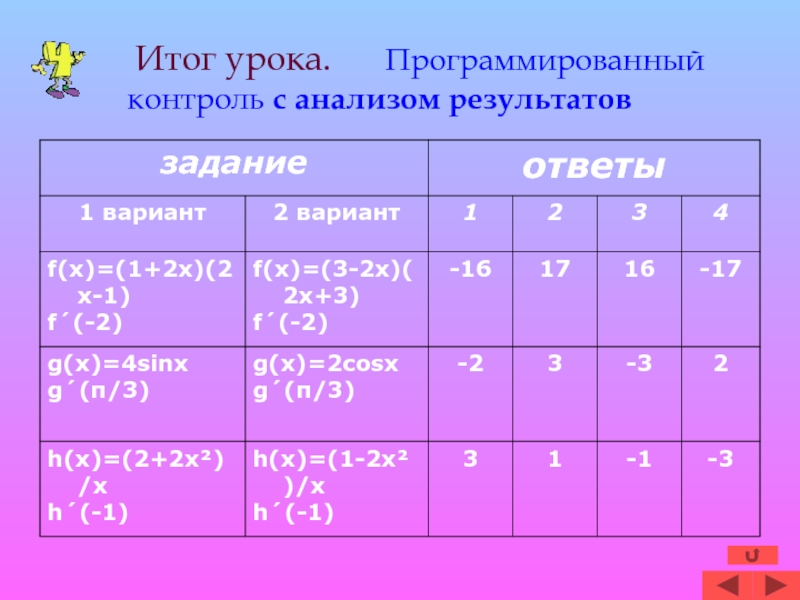
- 12. Итог урока. Программированный контроль с анализом результатов
- 13. Решение:Ответ: 1 вариант
- 14. Домашнее задание:Повторить п.13,17,
- 15. ИСААК
- 16. После окончания сельской школы родные послали его
- 17. Слайд 17
- 18. В Берлине был подготовлен труд Аналитическая механика
- 19. ССЫЛКИ http://test.allbest.ru/test.php- тесты
- 20. Оборудование:1.Компьютер2.Проектор3.Магнитная доска для графиков
- 21. Данная презентация была создана на курсах повышения
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема: Обобщение и систематизация знаний по теме «Производная»10класс
Выполнила: учитель математики
МОУ СОШ с. Пластинки Усманского района
Слайд 2
тип урока: обобщающий
Цели урока:
Систематизировать и обобщить знания о
производной функции;
Развить и углубить знания о производной;
Воспитывать интерес к математическому
анализу, культуру счёта, внимание.
Слайд 3
Содержание:
Проверка домашнего задания(фронтальный опрос)
Техника дифференцирования
Разбор подходов решения
Итог урока
( программированный контроль),
( программированный контроль), домашнее задание
Слайд 4Проверка домашнего задания
1. Сформулируйте определение производной функции в точке.
2.Пользуясь определением
производной, найдите f ‘(x),если:
Слайд 53. Поясните геометрический и механический смысл производной
4. Что можно утверждать,
глядя на график изображённой функции?
5. Как вы понимаете, что функция
непрерывна в точке ? Приведите примеры непрерывных функций. Какая между существует связь между непрерывностью функции и дифференцируемостью функции в этой точке?
Слайд 66.Перечислить формулы и правила дифференцирования:
а) тригонометрических функций;
б)степенной и сложной функции;
в)
правила дифференцирования
7.Вспомните, кто впервые ввёл термин « производная»?
Слайд 7
Итак, мы обобщили основные положения по теме
«Производная», а теперь выполним следующее задание. Расшифруйте, как И.Ньютон называл
производную функции.Техника дифференцирования
Слайд 9 Разбор подходов решения
по теме
Решить неравенства: а) h‘ (x)>0?если
Решение:
0
4
+
-
+
Ответ:(-∞;0)U(4;+∞)
Слайд 113. Заданы функции f(x)=3-2x¸g(x)=x² и p(x)=sinx. Задайте формулой сложную функцию
h ,если :
А)h(x)=f(g(x)) б)h(x)=g(p(x))
в)h(x)=p(f(x))h(x)=3-2x² h(x)=(sinx)² h(x)=sin(3-2x)
4Найдите область определения функции y=√sinx-0¸5
D(√)=[0;+∞) sinx-0¸5≥0¸sinx≥½
X1=arcsin½+2πn¸x=π/6+2πn, x2=π-π/6+2πn=5π/6+2πn¸
n Z
π/6+2πn ≤ x≤5π/6+2πn¸n Z
Ответ:[π/6+2πn;5π/6+2πn¸n Z]
Слайд 15 ИСААК НЬЮТОН
Этот человек сформулировал
основные законы механики,
открыл закон всемирного
тяготения, открыл законы
разложения белого цвета
выдвинул корпускулярно-волновую
теорию света, разработал дифференциальное и интегральное исчисления, открыл закон охлаждения нагретого тела, сконструировал один из первых термометров, впервые построил отражательный телескоп. Лагранж скажет о нём: «Он самый счастливый - систему мира можно установить только один раз.»
Он родился вьюжной зимой 1642 года, после рождества, когда метель особенно тоскливо выла в высоких каминных трубах Вулсторпа. Родился до срока, таким хилым и слабым, что местный священник считал, что он не жилец на этом свете. Но слабый этот младенец выжил всем на удивление и, странно, за всю свою долгую жизнь почти никогда не болел, к 84 годам потерял лишь один зуб.
Слайд 16После окончания сельской школы родные послали его продолжать образование в
Королевскую школу в Грэнтэм -маленький городок в10 километрах от родной
деревушки.Студентом Кембриджского университета Ньютон стал лишь в 1664 году. Учился средне, ничем замечательным себя не выказывал, хотя и был прилежным, интересовался математикой. Потом, спасаясь от ужасов чумы, он уезжает на два года в родную деревушку. Там он работает сверх всякой меры. В домике с крутой крышей рождаются дифференциальное и интегральное исчисления. Здесь. на грубом деревенском столе он раскладывает линзой солнечный луч, познавая тайну спектра. Здесь, под этими окнами, росла самая знаменитая в мире яблоня, с которой однажды с глухим стуком упало самое знаменитое в мире яблоко, подсказав Ньютону закон всемирного тяготения.» Всё это происходило в два чумных года-1665-й и 1666-й,-пишет Ньютон,- ибо в это время я был в расцвете изобретательских сил, и думал о математике и философии больше, чем когда –либо.
Слайд 17
ЛАГРАНЖ, ЖОЗЕФ ЛУИ) (1736– 1813),
французский математик и механик. Родился 25 января 1736
в Турине. Учился в Туринском университете .Стал
профессором геометрии в Артиллерийской школе Турина. В
1755 Лагранж послал Эйлеру свою
работу об изопериметрических свойствах, ставших
впоследствии основой вариационного исчисления. В 1756 по
представлению Эйлера стал иностранным членом Берлинской
Академии наук. Принимал участие в организации в Турине
научного общества (впоследствии Туринской Академии наук). В 1764 Парижская
Академия наук объявила конкурс на лучшую работу по проблеме движения Луны.
Лагранж представил работу, посвященную либрации Луны, которая была
удостоена первой премии. В 1766 получил вторую премию Парижской Академии за
исследование, посвященное теории движения спутников Юпитера, а до 1778 был
удостоен еще трех премий. В 1766 по приглашению Фридриха II Лагранж переехал
в Берлин, где стал президентом Берлинской Академии наук. Берлинский период
(1766–1787) был самым плодотворным в жизни Лагранжа. Здесь он выполнил
важные работы по алгебре и теории чисел, а также по решению
дифференциальных уравнений в частных производных.
Слайд 18В Берлине был подготовлен труд Аналитическая механика опубликованный в Париже
в 1788 и ставший вершиной научной деятельности Лагранжа. В основу
всей статики положен т.н. принцип возможных перемещений, в основу динамики – сочетание этого принципа с принципом Д'Аламбера. Введены обобщенные координаты, разработан принцип наименьшего действия.В 1787, после кончины Фридриха II, Лагранж переехал в Париж и стал членом
комиссии, занимавшейся разработкой метрической системы мер и весов и нового
Парижской Академии наук. Во время Французской революции принял участие в работе календаря. В 1797, после создания Политехнической школы, вел преподавательскую деятельность, читал курс математического анализа. В 1795, после открытия Института Франции, стал главой его физико-математического класса.
Лагранж внес существенный вклад во многие области математики, включая
вариационное исчисление, теорию дифференциальных уравнений, решение задач на
нахождение максимумов и минимумов, теорию чисел (теорема Лагранжа), алгебру и
теорию вероятностей. В двух своих важных трудах – Теория аналитических функций
(Théorie des fonctions analytiques, 1797) и О решении численных уравнений (De la
résolution des équations numériques, 1798) – подытожил все, что было известно по этим вопросам в его время, а содержавшиеся в них новые идеи и методы были развиты в работах математиков 19 в.
Умер Лагранж в Париже 10 апреля 1813.