Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку алгебры 8 класс "Квадратные уравнения"
Содержание
- 1. Презентация к уроку алгебры 8 класс "Квадратные уравнения"
- 2. ЗНАНИЯ – ВАМ ОЧЕНЬ НУЖНЫ;УМЕНИЕ – ЦЕННЕЙШЕЕ КАЧЕСТВО;ОПЫТ – В ЖИЗНИ НЕОБХОДИМ!
- 3. Образовательные: закрепление и обобщение знаний учащихся полученные
- 4. уравнение вида ах2 + вх +с =
- 5. Слайд 5
- 6. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯКВАДРАТНЫЕ УРАВНЕНИЯа ≠
- 7. а) 6х2 – х + 4 =
- 8. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с
- 9. Решение неполных квадратных уравненийax2 + bx +
- 10. РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :1 вариант:а)
- 11. Исторические сведения:Квадратные уравнения впервые встречаются в работе
- 12. Решение задачи Бхаскары:Пусть было x
- 13. История развития квадратных
- 14. Квадратные уравнения в Багдаде (9 век):Впервые квадратные
- 15. Квадратные уравнения в Древнем Вавилоне:Необходимость решать
- 16. Квадратные уравнения в ИндииЗадачи на квадратные уравнения
- 17. Квадратные уравнения в Европе в 13-17 веках:Формулы
- 18. Виды квадратных уравненийНеполные квадратные уравнения и частные
- 19. Выводы: Впервые квадратные уравнения
- 20. СПАСИБО ЗА УРОК!
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 учитель Сафронова В. А.
АЛГЕБРА, 8 класс
Тема урока:
«Квадратные уравнения»
МБОУ Токарёвской СОШ №1 в с Троицкий РосляйСлайд 3Образовательные: закрепление и обобщение знаний учащихся полученные при изучении темы,
отработка умений и навыков по решению квадратных уравнений различного вида
различными способами, выработка умения выбрать нужный рациональный способ решения.Развивающие: развитие логического мышления, памяти, внимания, умений сравнивать и обобщать, умения выступать с самостоятельными суждениями и отстаивать их.
Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры, умение работать в группах, развивать познавательную активность и логическое мышление учащихся, развития интереса к предмету.
Цель урока:
Слайд 4
уравнение вида ах2 + вх +с = 0,
где
х –переменная,
а, в и с некоторые числа,
причем
а 0.ОПРЕДЕЛЕНИЕ:
Квадратным уравнением называется
Слайд 5 Квадратным уравнением называется
уравнение вида
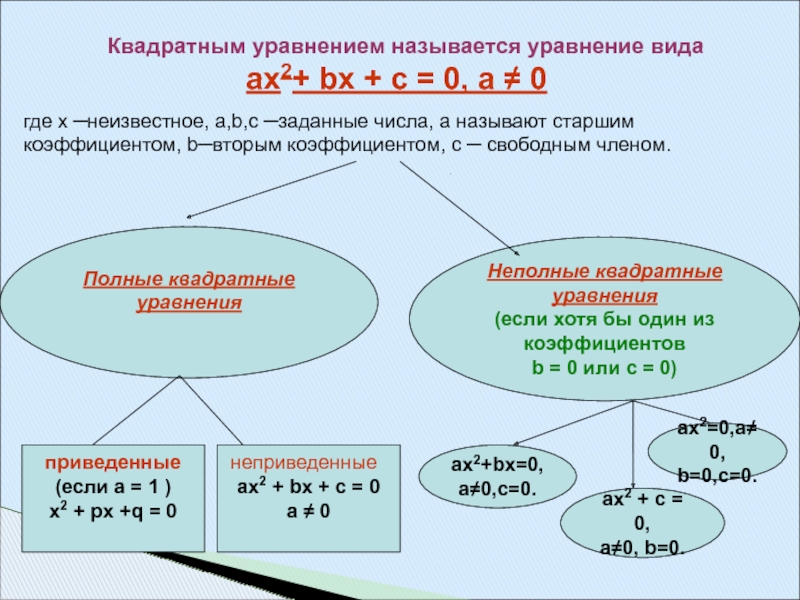
ax2+ bx + c = 0, а ≠ 0где х ─неизвестное, a,b,c ─заданные числа, а называют старшим коэффициентом, b─вторым коэффициентом, c ─ свободным членом.
Неполные квадратные уравнения
(если хотя бы один из коэффициентов
b = 0 или c = 0)
Полные квадратные уравнения
приведенные
(если а = 1 )
х2 + px +q = 0
ax2 + bx + c = 0
а ≠ 0
неприведенные
ax2 + c = 0,
a≠0, b=0.
ax2=0,a≠0,
b=0,c=0.
ax2+bx=0,
a≠0,c=0.
Слайд 6
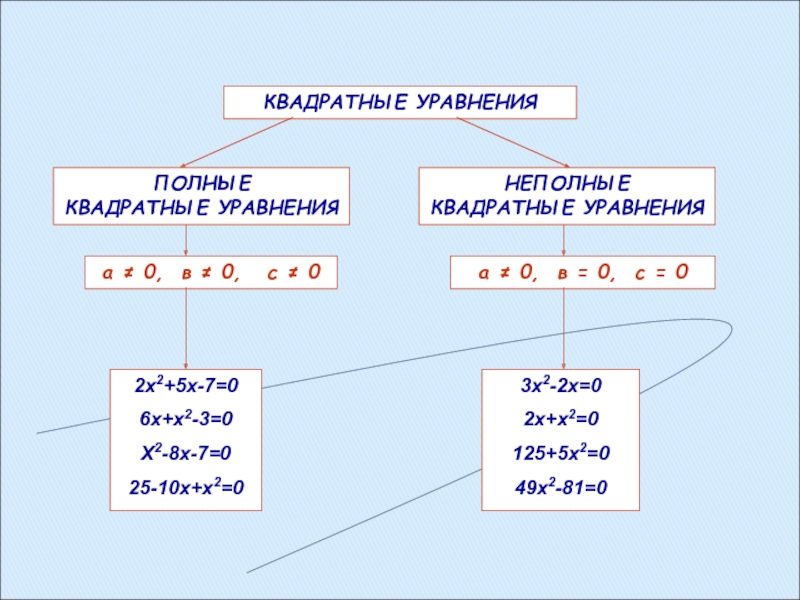
ПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠ 0,
с ≠ 0
а ≠ 0, в = 0, с =
02х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 7
а) 6х2 – х + 4 = 0
б) 12х -
х2 + 7 = 0
в) 8 + 5х2 = 0
г)
х – 6х2 = 0д) - х + х2 = 15
а = 6, в = -1, с = 4;
а = -1, в = 12, с = 7;
а = 5, в = 0, с = 8;
а = -6, в =1, с = 0;
а = 1, в =-1, с = -15.
Определите коэффициенты
квадратного уравнения:
Слайд 8
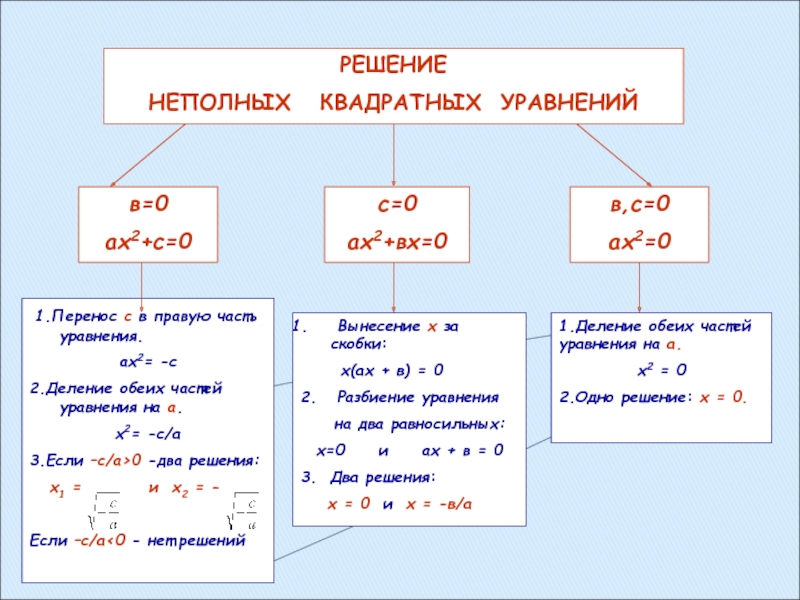
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в правую часть
уравнения.
ах2= -с
2.Деление обеих частей уравнения на а.
х2= -с/а
3.Если –с/а>0 -два
решения:х1 = и х2 = -
Если –с/а<0 - нет решений
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 9Решение неполных квадратных уравнений
ax2 + bx + c = 0,
а ≠ 0
Если b≠0, а с=0,то
ax2+bx=0,
х·(ах + b)=0,
x = 0,
ах + b = 0,ах = -b,
х = -
Если b=0, а с≠0,то
ax2+ с = 0,
ах2 = -с,
х2 = -
Если b=0,с = 0,
ах2 = 0,
х = 0
-
>
0,то
х =±
-
<0,то
корней
нет.
Слайд 10
РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :
1 вариант:
а)
б) ( х + 2)2 + ( х -3)2 = 13
2 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0
3 вариант:
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0
Слайд 11
Исторические сведения:
Квадратные уравнения впервые встречаются в работе индийского математика и
астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило
решения квадратных уравнений, которое практически совпадает с современным.В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Слайд 12
Решение задачи Бхаскары:
Пусть было x обезьянок,
тогда на
поляне забавлялось – .
Составим уравнение:
+ 12 = хОтвет: х1= 16 , х2= 48 обезьянок.
Слайд 13История развития квадратных
уравнений:
Квадратные
уравнения в Багдаде(9 век).
Квадратные уравнения в Древнем Вавилоне.
Квадратные уравнения
в Индии.Квадратные уравнения в Европе 13 -17в.в.
Слайд 14Квадратные уравнения в Багдаде (9 век):
Впервые квадратные уравнения
появились в городе
Багдаде, их вывел приглашённый математик из Хорезм(Ныне территория Узбекистана) Мухаммед
бен-Муса Ал-Хорезми. В отличие от греков, решавших квадратные уравнения геометрическим путем, он мог решить любые квадратные уравнения по общему правилу (найти положительные корни). Если у греков было геометрическое решение, то метод Ал-Хорезми почти алгебраический.Слайд 15 Квадратные уравнения в Древнем Вавилоне:
Необходимость решать уравнения не только
первой, но и второй степени ещё в древности была вызвана
потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а так же с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: х2 + х = х2 ─ х =Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила, Почти все найденные до сих пор клинописные тексты, приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены, Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.
Слайд 16Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в
499 году.
В Древней Индии были распространены публичные соревнования в решении
трудных задач.В одной из старинных индийских книг говорится по поводу таких соревнований следующее: “Как солнце блеском своим затмевает звёзды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические
задачи”.
Слайд 17
Квадратные уравнения в Европе в 13-17 веках:
Формулы решения квадратных уравнений
в Европе были
Впервые изложены в 1202 году итальянским математиком
Леонардо
Фибоначчи.Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду аx2 + bx + c = 0,было
Сформулировано в Европе лишь в 1544
Году немецким математиком
Михаэлем Штифелем.
Слайд 18Виды квадратных уравнений
Неполные квадратные уравнения и частные виды полных квадратных
Уравнений
(х2 + х = а) умели решать Некоторые виды квадратных
уравнений решали древнегреческие математики, сводя их решение к геометрическим построениям. Правило решения квадратных уравнений, приведенных к видуaх2 + bx + c = 0, где а ≠ 0,дал индийский ученый Брахмагупта(7век).
Вывод формулы корней квадратного уравнения в общем виде имеется у Виета, однако он признавал только положительные корни. Итальянские математики 16 веке учитывают помимо положительных и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.
Слайд 19 Выводы:
Впервые квадратные уравнения сумели решить математики
Древнего
Египта. Неполные квадратные уравнения умели решать вавилоняне
(около 2 тыс. лет
до н.э.). Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Примеры решения уравнений без обращения к геометрии даёт Диофант Александрийский (III век).
Правило решения квадратных уравнений дал индийский учёный
Брахмагупта (VII век).
Общее правило решения квадратных уравнений было
Сформулировано немецким математиком М. Штифелем.
Выводом формулы решения квадратных уравнений общего вида занимался Ф. Виет.