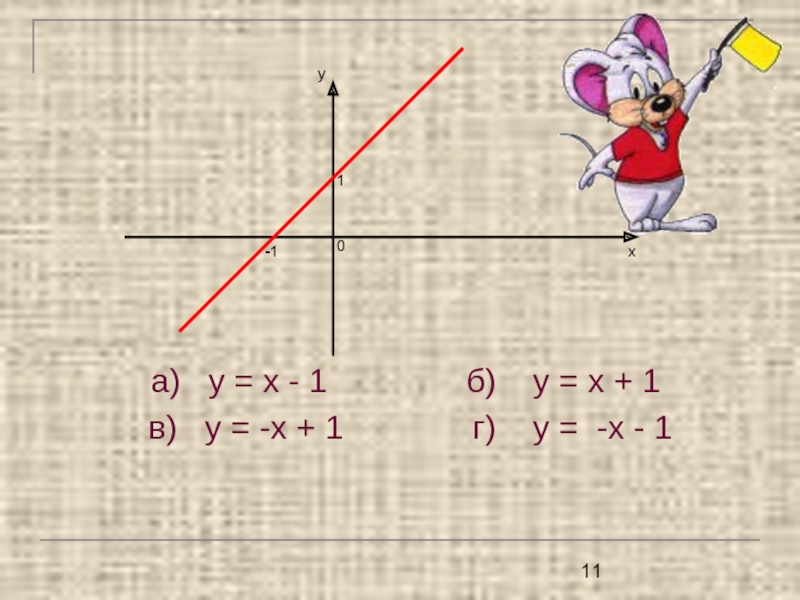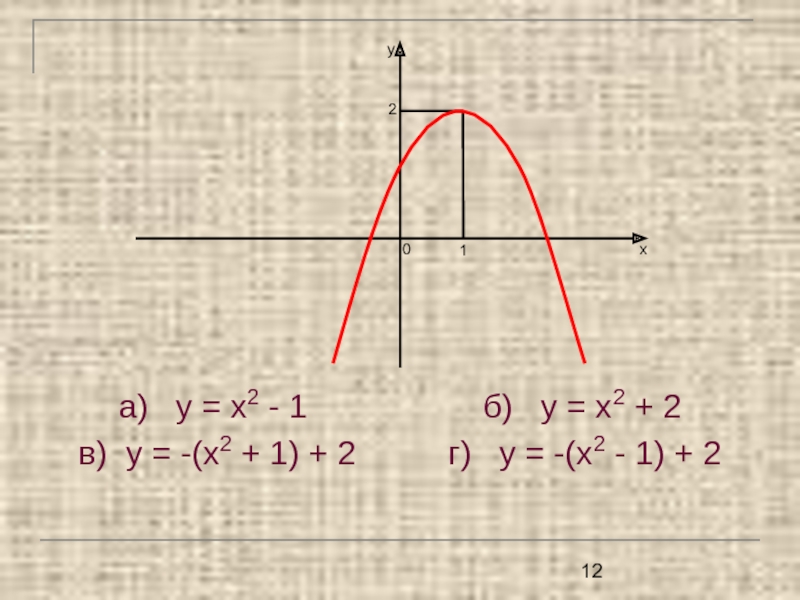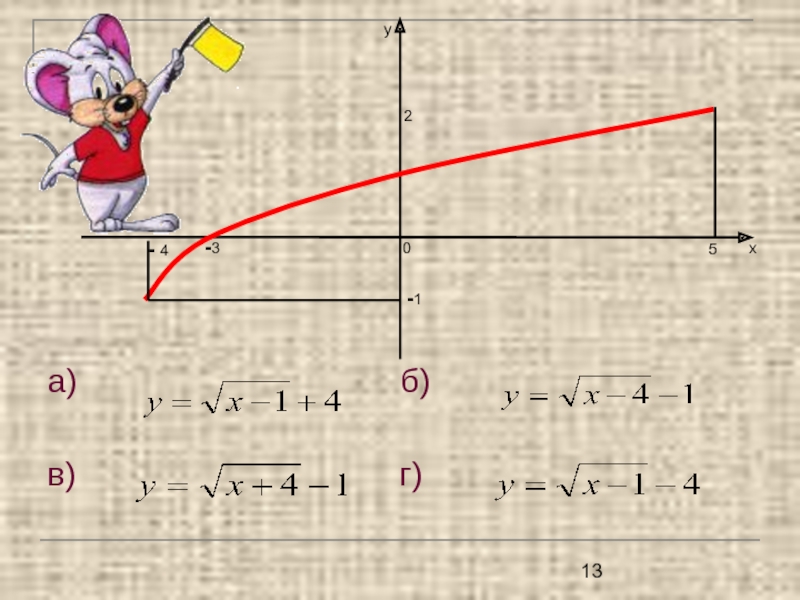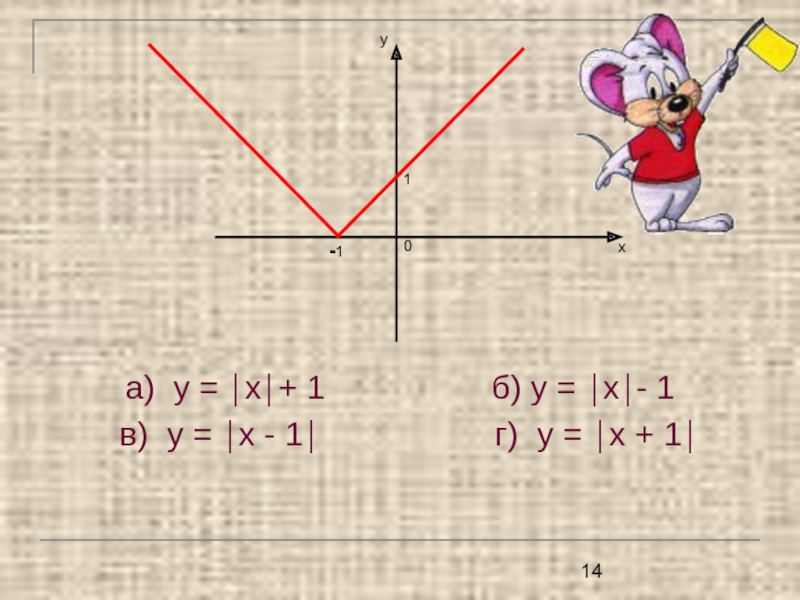Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и графики (9 класс)
Содержание
- 1. Функции и графики (9 класс)
- 2. Задачи урокаПовторить и закрепить умения:Строить и читать графики степенной функции;Графически решать уравнения, неравенства, системы.
- 3. Понятие функции. у = f(x)Укажите закон образования
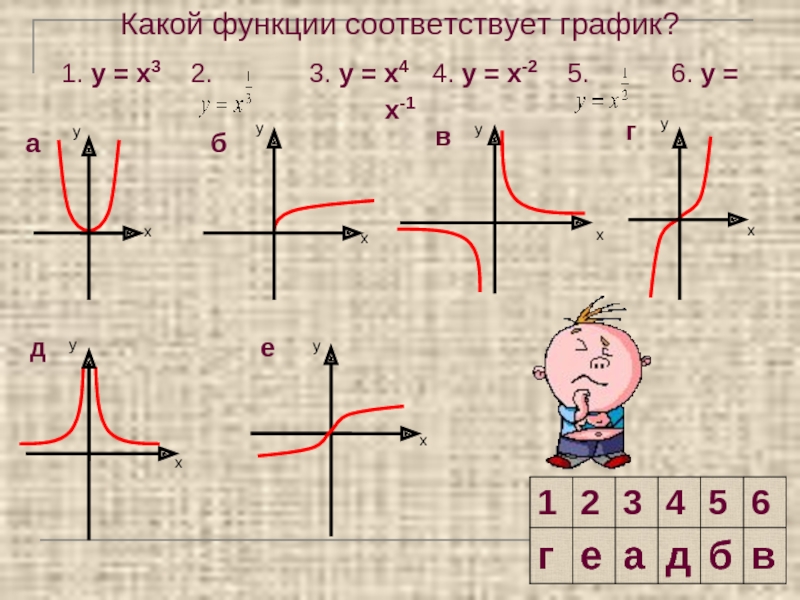
- 4. Какой функции соответствует график? 1. у =
- 5. Найти область определения функции: а) (- ∞;
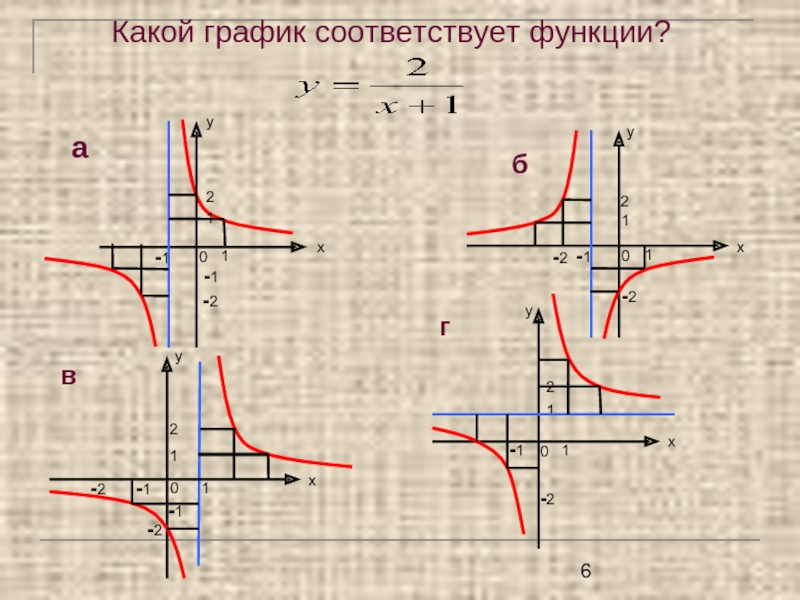
- 6. Какой график соответствует функции?
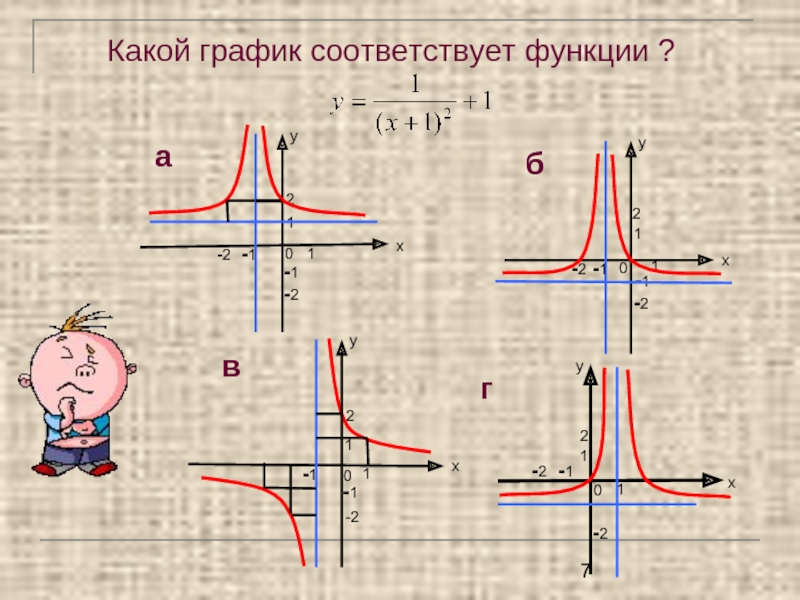
- 7. Какой график соответствует функции ?
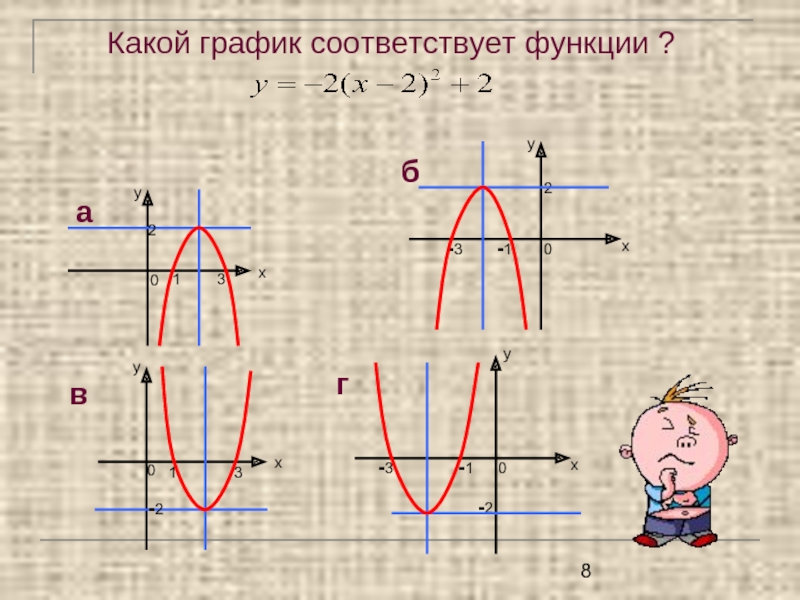
- 8. Какой график соответствует функции ?
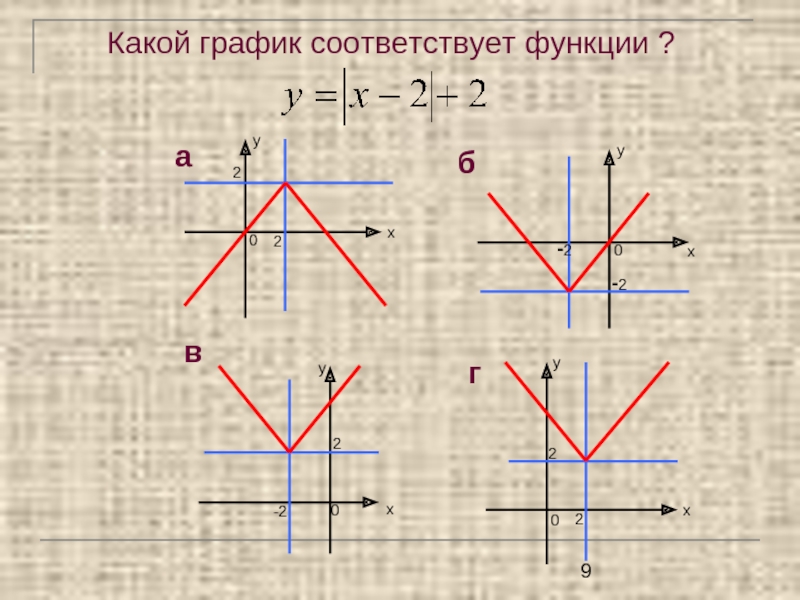
- 9. Какой график соответствует функции ?
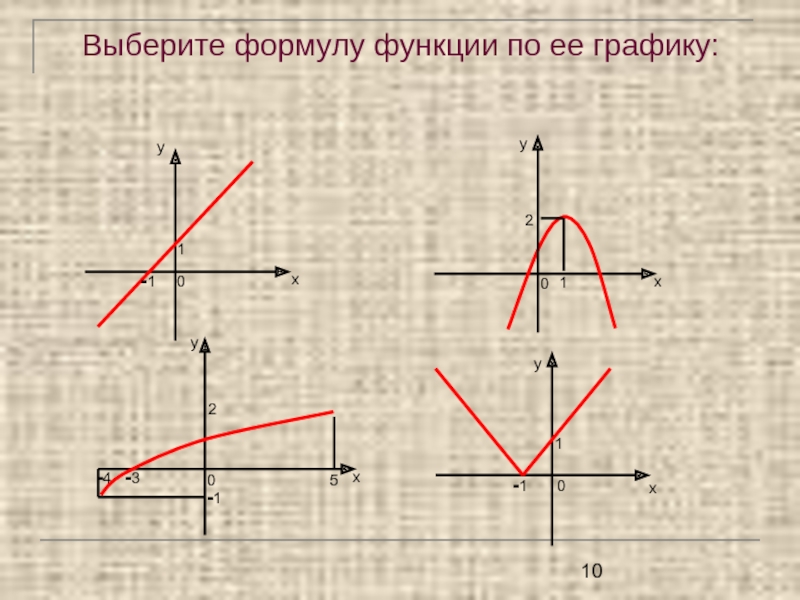
- 10. Выберите формулу функции по ее графику:
- 11. а) у = х - 1
- 12. а) у = х2 - 1
- 13. а)
- 14. а) у = ⏐х⏐+ 1
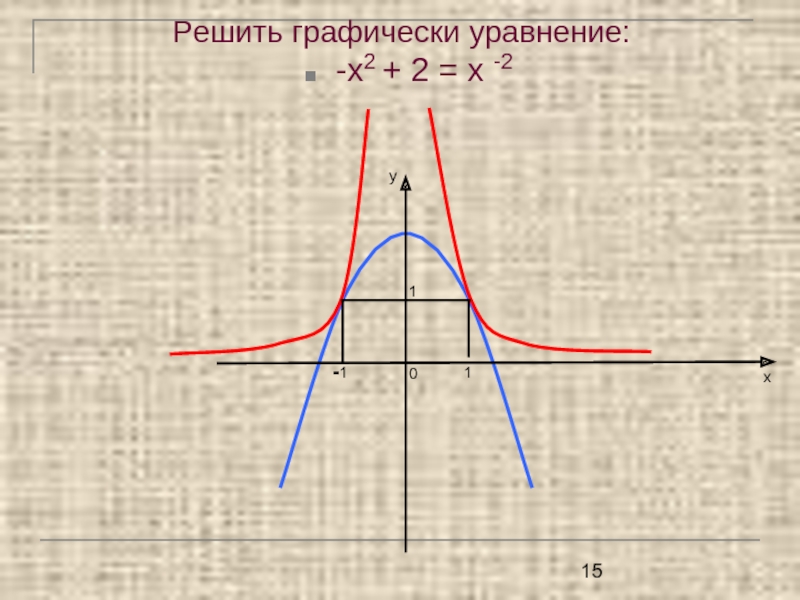
- 15. Решить графически уравнение:-х2 + 2 = х -2
- 16. Решить графически неравенство: ух-11/////////////////////////////////////////0
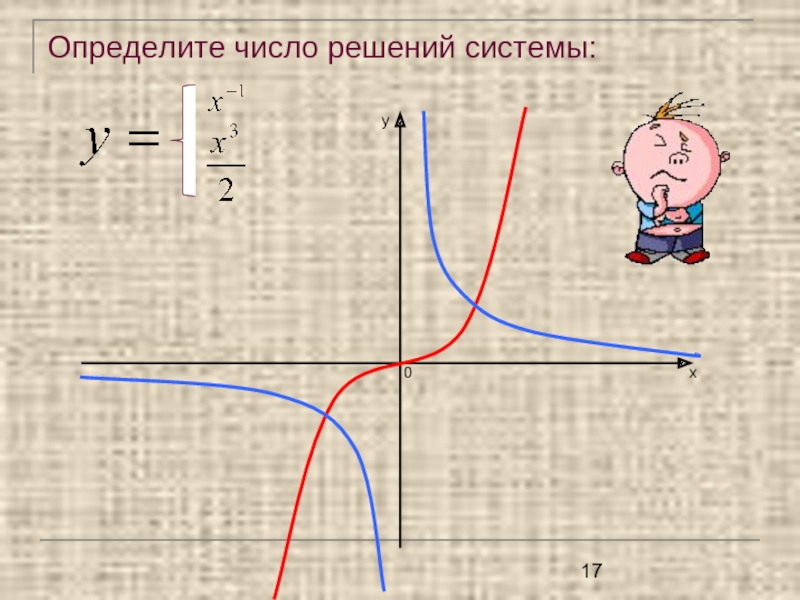
- 17. Определите число решений системы: ух0
- 18. Постройте и прочитайте график функции: ⏐x⏐,
- 19. Укажите число корней уравнения f(x)=p, где
- 20. Показать на графике область, удовлетворяющую системе неравенств:
- 21. Что мы должны уметь:Уметь строить график степенной
- 22. Скачать презентанцию
Задачи урокаПовторить и закрепить умения:Строить и читать графики степенной функции;Графически решать уравнения, неравенства, системы.
Слайды и текст этой презентации
Слайд 2Задачи урока
Повторить и закрепить умения:
Строить и читать графики степенной функции;
Графически
решать уравнения, неравенства, системы.
Слайд 5Найти область определения функции:
а) (- ∞; 1,5);
б)(-
∞; -4] ∪ (5;+∞)
в)(- ∞; -2] ∪[0.5;+∞)
г) (
-∞; +∞); 1.
2.
3.
4.
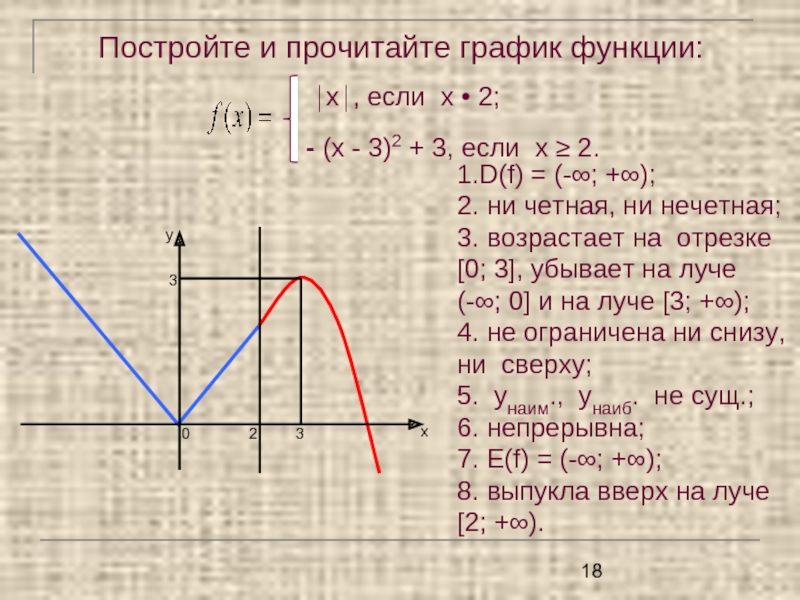
Слайд 18Постройте и прочитайте график функции: ⏐x⏐, если х • 2;
- (х - 3)2 + 3, если х ≥ 2.
1.D(f) = (-∞; +∞);
2. ни четная, ни нечетная;
3. возрастает на отрезке
[0; 3], убывает на луче
(-∞; 0] и на луче [3; +∞);
4. не ограничена ни снизу, ни сверху;
5. унаим., унаиб. не сущ.;
6. непрерывна;
7. Е(f) = (-∞; +∞);
8. выпукла вверх на луче [2; +∞).
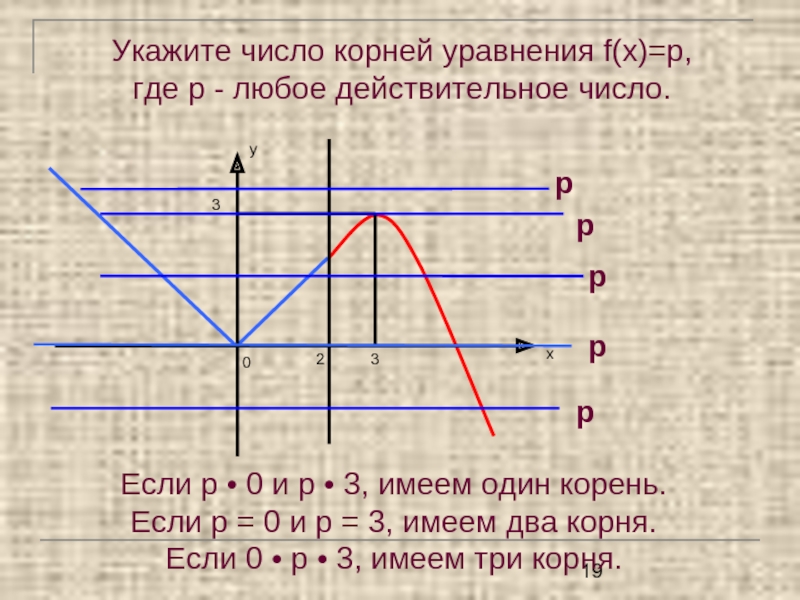
Слайд 19Укажите число корней уравнения f(x)=p, где p - любое действительное
число.
Если р • 0 и р • 3, имеем один
корень. Если р = 0 и р = 3, имеем два корня.
Если 0 • р • 3, имеем три корня.
Слайд 20Показать на графике область, удовлетворяющую системе неравенств: х2 + у2
≥ 1,
х2 + у2 ≤ 9.
х
3
1
у
3
0
Слайд 21Что мы должны уметь:
Уметь строить график степенной функции.
Уметь по графику
составлять формулы функции.
Уметь строить и читать кусочные функции.
Уметь графически решать
уравнения, неравенства и их системы.
Теги



![Функции и графики (9 класс) Найти область определения функции: а) (- ∞; 1,5); б)(- ∞; -4] Найти область определения функции: а) (- ∞; 1,5); б)(- ∞; -4] ∪ (5;+∞) в)(- ∞; -2] ∪[0.5;+∞)](/img/thumbs/bb617ff1ebd3671ed45b3b1d82197671-800x.jpg)