Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение интеграла в геометрии
Содержание
- 1. Применение интеграла в геометрии
- 2. Цель проекта: Показать применение интеграла при вычислении объёмов тел
- 3. Общая формула для объема тела вращения Пусть
- 4. объем конуса Дано: y=kx ; x=0 ;
- 5. Объём шара V =
- 6. Шаровым сегментом называется часть шара, отсекаемая от
- 7. Объём (треугольной) наклонной призмыАВСААВВСС111222ООХХ1АВСА1В1С1 – наклонная призмаОО1
- 8. Объём пирамидыОбъём пирамиды равен одной
- 9. ВыводОбъёмы различных тел мы вычисляли опираясь
- 10. Используемые источники:Колмогоров А. Н., Алгебра и начала
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Общая формула для объема тела вращения
Пусть криволинейная трапеция опирается
на отрезок [a;b] оси Ox и ограничена сверху графиком функции
f, неотрицательной и непрерывной на отрезке от [a;b]. При вращении этой криволинейной трапеции вокруг оси Ox получили тело, объем которого находится по формуле:V= ƒ²(x)dx
Действительно, каждая плоскость перпендикулярная оси Ох и пересекающая отрезок [a;b] этой оси в точке х, дает в сечении с телом круг с радиусом ƒ(x) и площади S(x)= ƒ²(x)
Sкр= R² ; R=ƒ(x) S(x)= ƒ²(x)
V= S(x)dx= ƒ²(x)dx
Слайд 4
объем конуса
Дано: y=kx ; x=0 ; x=h ; y=0
Криволинейная трапеция
ox-ось вращенияДоказать: V= 1/3Sh
x
y
0
y=kx
h
r
Доказательство: y=kx ; R=tg r/h
V = (2/hx)²dx = r²/h²·x³/3 | = r²/h²·h³/3 = 1/3 r²h = 1/3Sh
т
h
0
o
h
π
V= ƒ²(x)
Слайд 5Объём шара
V = ƒ²(x)dx
-R
R
y =
Шар получается путём вращения полукруга вокруг диаметра.
y =
X = -R
x = R
y = o
Криволинейная трапеция
Vт.вр. = ƒ²(x)dx
ƒ(х) = ; Vм = 2 (R²-x²)dx = 2 (R²x-x³/3) | 2 (R²-R³/3) = 2 ·2R³/3 =
4/3 R³
т
R
o
o
R
Слайд 6
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
y
x
R
0
h
R
y=
Vт.вр
=
a = R-h,
b = RVш.сегм.= (R²-x²)dx= (R²x-x²/3)| =
((R³-R³/3)-(R²(R-h)-(R-h)³/3))=
ƒ²(x)dx ; ƒ(x) =
x²
R²
−
R
R-h
(2/3R³-(R³-R²h-1/3(R³-3R²h+3Rh²-h³))= (2/3R³-(R³-R²h-1/3R³+R²h-Rh²+h³/3))=
= (2/3R³-R³+R²h+1/3R³-R²h+Rh²-1/3h³)= (Rh²-1/3h³)= h²(R-1/3h)
π
Слайд 7Объём (треугольной) наклонной призмы
А
В
С
А
А
В
В
С
С
1
1
1
2
2
2
О
О
Х
Х
1
АВСА1В1С1 – наклонная призма
ОО1 = h
OХ
(АВС)
(А2В2С2) – сечение
(А2В2С2) Ох
(А2В2С2) Ox = x
S
(x) = SABC т.к. ∆АВС = ∆А2В2С2 по СССт.к. А2АВ2В ; ВВ2С2С – параллелограммы
V = = = Sx | = Sh
Т
Т
U
Замечания:
объём произвольной наклонной призмы равен сумме объёмов треугольных призм:
V = V1 + V2 + Vn = S1h + S2h + … Snh = h ( S1 + S2 + …Sn ) = Sh
Объём наклонной призмы равен произведению бокового ребра на площадь сечения призмы плоскостью, перпендикулярной к боковым рёбрам и пересекающей их.
h
0
Слайд 8
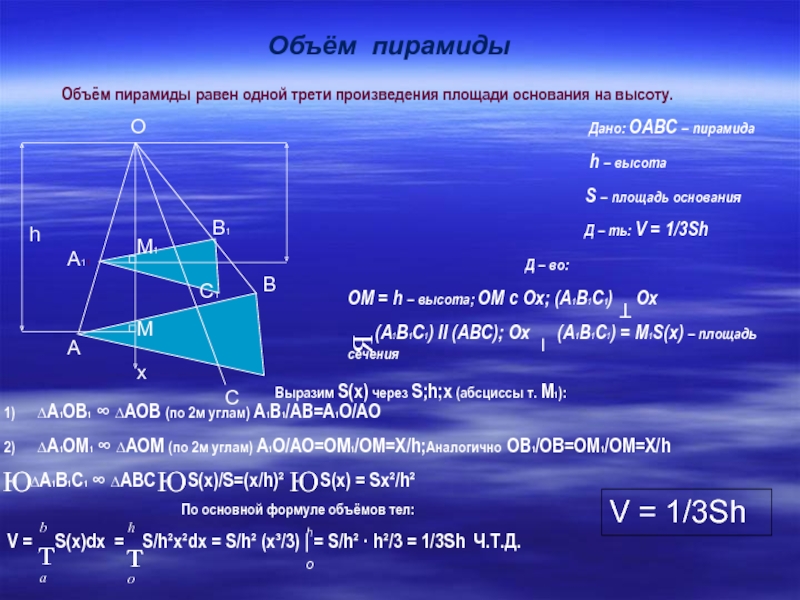
Объём пирамиды
Объём пирамиды равен одной трети произведения площади
основания на высоту.
В
С
А
В1
С1
М
О
h
М1
A11
x
Дано: OABC – пирамидаh – высота
S – площадь основания
Д – ть: V = 1/3Sh
Д – во:
ОМ = h – высота; ОМ с Ох; (А1В1С1) Ох
(А1В1С1) II (АВС); Ох (А1В1С1) = М1S(x) – площадь сечения
Т
∆А1ОВ1 ∞ ∆АОВ (по 2м углам) А1В1/AB=A1O/AO
∆А1ОM1 ∞ ∆АОM (по 2м углам) A1O/AO=ОМ1/OM=X/h;Аналогично ОВ1/OB=ОМ1/OM=X/h
∆А1В1C1 ∞ ∆АВC S(x)/S=(x/h)² S(x) = Sx²/h²
По основной формуле объёмов тел:
V = S(x)dx = S/h²x²dx = S/h² (x³/3) | = S/h² · h²/3 = 1/3Sh Ч.Т.Д.
Выразим S(x) через S;h;x (абсциссы т. М1):
o
h
V = 1/3Sh
Слайд 9 Вывод
Объёмы различных тел мы вычисляли опираясь на основную формулу
объёмов тел с помощью интеграла.
Это является ещё одним
подтверждением того, что определённый интеграл есть некоторый фундамент для изучения математики.Слайд 10Используемые источники:
Колмогоров А. Н., Алгебра и начала анализа [Текст]: Учеб.
для 10-11 кл. общеобразоват. учреждений/ – М.: Просвещение, 1998 –
365 c.Мордкович А. Г., Алгебра и начала анализа [Текст]: Учеб. для 10-11 кл. общеобразоват. учреждений. Ч. I. – М.: Мнемозина, 2003. – 375 с.
Интернет – ресурсы
http://imc.rkc-74.ru/dlrstore/3/3a53fd3a-03cb-22b0-4cc0-abce209c671b/0003248G.htm
Изображения многогранников. б – пирамида с треугольными гранями и
квадратным основанием; в – треугольная призма; г – пятиугольная
призма; д – р-угольная антипризма;


![Применение интеграла в геометрии Общая формула для объема тела вращения Пусть криволинейная трапеция опирается на Общая формула для объема тела вращения Пусть криволинейная трапеция опирается на отрезок [a;b] оси Ox и ограничена](/img/thumbs/0ba221b8153a2e977883c31ac3db9031-800x.jpg)





![Применение интеграла в геометрии Используемые источники:Колмогоров А. Н., Алгебра и начала анализа [Текст]: Учеб. для Используемые источники:Колмогоров А. Н., Алгебра и начала анализа [Текст]: Учеб. для 10-11 кл. общеобразоват. учреждений/ – М.:](/img/thumbs/449eeb1df6c160d194f2cfe228a08d67-800x.jpg)