Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к исследованию функций 10 класс
Содержание
- 1. Применение производной к исследованию функций 10 класс
- 2. Непрерывность функции
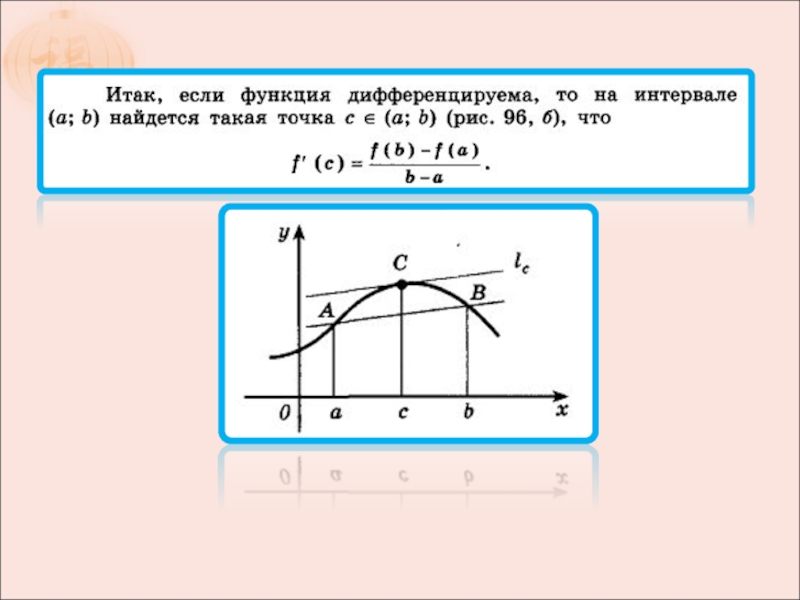
- 3. Если функция непрерывна в каждой точке промежутка
- 4. Слайд 4
- 5. Касательная к графику функции
- 6. Производная функции f’(x) – это угловой коэффициент касательной к графику функции f(x)
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Признаки возрастания и убывания функции
- 11. Если f’(x) > 0 в каждой точке
- 12. Слайд 12
- 13. Критические точки Экстремумы функции
- 14. Внутренние точки области определения функции, в которых
- 15. Пьер ФермаЕсли точка xo является точкой экстремума
- 16. Признак максимума функцииЕсли функция f непрерывна в
- 17. Признак минимума функцииЕсли функция f непрерывна в
- 18. Находим f ‘(x)Определяем критические точки функции f(x),
- 19. Находим максимум и минимумНаходим экстремальные значения функции
- 20. Слайд 20
- 21. Наибольшее и наименьшее значение функции
- 22. Теорема ВейерштрассаКарл ВейерштрассЕсли на отрезке [a;b] функция
- 23. Алгоритм нахождения наибольшего и наименьшего значения функции
- 24. ЧАСТНЫЙ СЛУЧАЙЕсли функция не имеет критических точек,
- 25. Слайд 25
- 26. ДОМАШНЕЕ ЗАДАНИЕЗадания по карточкамПовторить основные алгоритмы и понятия
- 27. Скачать презентанцию
Непрерывность функции
Слайды и текст этой презентации
Слайд 3Если функция непрерывна в каждой точке промежутка I, то её
называют непрерывной на этом промежутке
Функция f(x) непрерывна в точке x0
если f’(x) ≠ 0 Если на промежутке [ a ; b] функция непрерывна, то функция сохраняет свой знак
Слайд 11Если f’(x) > 0 в каждой точке интервала I, то
функция f возрастает на I
Если f’(x) < 0 в каждой
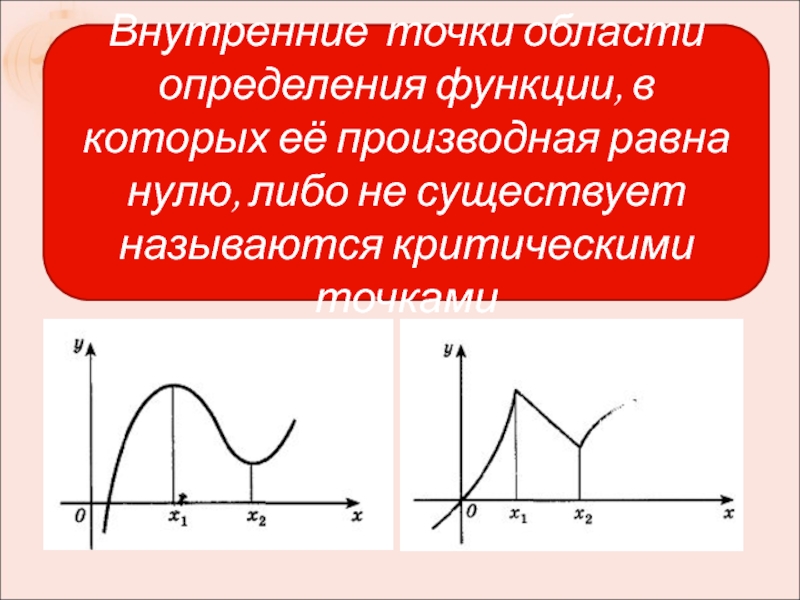
точке интервала I, то функция f убывает на I
Слайд 14Внутренние точки области определения функции, в которых её производная равна
нулю, либо не существует называются критическими точками
Слайд 15Пьер Ферма
Если точка xo является точкой экстремума функции f и
в этой точке существует её производная f’, то:
f’(x0) = 0
Необходимое
условие экстремума
Слайд 16Признак максимума функции
Если функция f непрерывна в точке x0, а
f’(x0) > 0 на интервале (a ; x0), и f’(x0)
< 0 на интервале (x0 ; b) , то точка x0 является точкой максимумаЕсли в точке x0 функция меняет знак с «+» на «-», то точка x0 является точкой максимума
Слайд 17Признак минимума функции
Если функция f непрерывна в точке x0, а
f’(x0) < 0 на интервале (a ; x0), и f’(x0)
> 0 на интервале (x0 ; b) , то точка x0 является точкой минимумаЕсли в точке x0 функция меняет знак с «-» на «+», то точка x0 является точкой минимума
Слайд 18Находим f ‘(x)
Определяем критические точки функции f(x), т.е. точки, в
которых f ‘(x)=0 . Располагаем их в порядке возрастания.
Определяем знак
f ‘(х) на каждом из промежутков (а;в) в критических точкахАлгоритм нахождения экстремумов функции
Слайд 19Находим максимум и минимум
Находим экстремальные значения функции в точках максимум
и минимум
Если не указан интервал, на котором исследуется функция у=f(х)
на экстремум, то вначале следует найти область ее определения.Алгоритм нахождения экстремумов функции
Слайд 22Теорема Вейерштрасса
Карл Вейерштрасс
Если на отрезке [a;b] функция непрерывна, то в
некоторых точках данного отрезка функция принимает своё наибольшее и наименьшее
значение![Теорема ВейерштрассаКарл ВейерштрассЕсли на отрезке [a;b] функция непрерывна, то в некоторых точках данного отрезка функция принимает своё](/img/thumbs/edb4cab86a711ea6591d726299fedbd8-800x.jpg "Применение производной к исследованию функций 10 класс Теорема ВейерштрассаКарл ВейерштрассЕсли на отрезке [a;b] функция непрерывна, то в некоторых")
Слайд 23Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке [a;b]
Найти
критические точки заданной функции
Найти значения функции в критических точках
Найти значение
функции на концах отрезкаИз получившихся значений выбрать наименьшее и наибольшее
![Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке [a;b]Найти критические точки заданной функцииНайти значения функции в](/img/thumbs/8af688f408ece41909facebec30ad859-800x.jpg "Применение производной к исследованию функций 10 класс Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке [a;b]Найти критические")
Слайд 24ЧАСТНЫЙ СЛУЧАЙ
Если функция не имеет критических точек, то функция либо
возрастает на отрезке [a;b],
либо убывает на отрезке [a;b]
Наибольшее и наименьшее
значение – значения функции на концах данного отрезка
![ЧАСТНЫЙ СЛУЧАЙЕсли функция не имеет критических точек, то функция либо возрастает на отрезке [a;b],либо убывает на отрезке](/img/thumbs/3b82d719fdcc21be3fb23eeb2536fbae-800x.jpg "Применение производной к исследованию функций 10 класс ЧАСТНЫЙ СЛУЧАЙЕсли функция не имеет критических точек, то функция либо возрастает")
