Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проектная работа по алгебре "Тригонометрия и ее применение в различных сферах науки и жизни"
Содержание
- 1. Проектная работа по алгебре "Тригонометрия и ее применение в различных сферах науки и жизни"
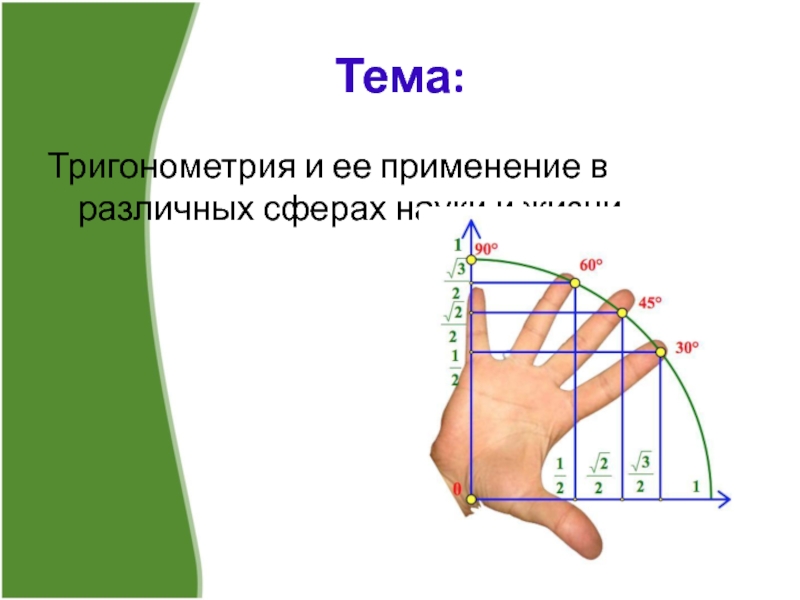
- 2. Тема:Тригонометрия и ее применение в различных сферах науки и жизни.
- 3. Проблема:Почему знания тригонометрии необходимы для современного человека?
- 4. Цель: Связь тригонометрии с реальной жизнью.Задачи: Изучить
- 5. Гипотеза: Тригонометрия применяется не только в
- 6. Тригонометрия- – (от греч. trigwnon – треугольник
- 7. Ранние века:От вавилонской математики ведёт начало
- 8. Древняя Греция:Общее и логически связное изложение тригонометрических
- 9. Средневековье: В IV веке, после гибели
- 10. Новое время:Развитие тригонометрии в Новое время стало
- 11. XVIII век:Современный вид тригонометрии придал Леонард Эйлер. В
- 12. Применение тригонометрии: Тригонометрия в биологии: Тригонометрия играет
- 13. Тригонометрия в 3D графике Аналог 3D, переводящая
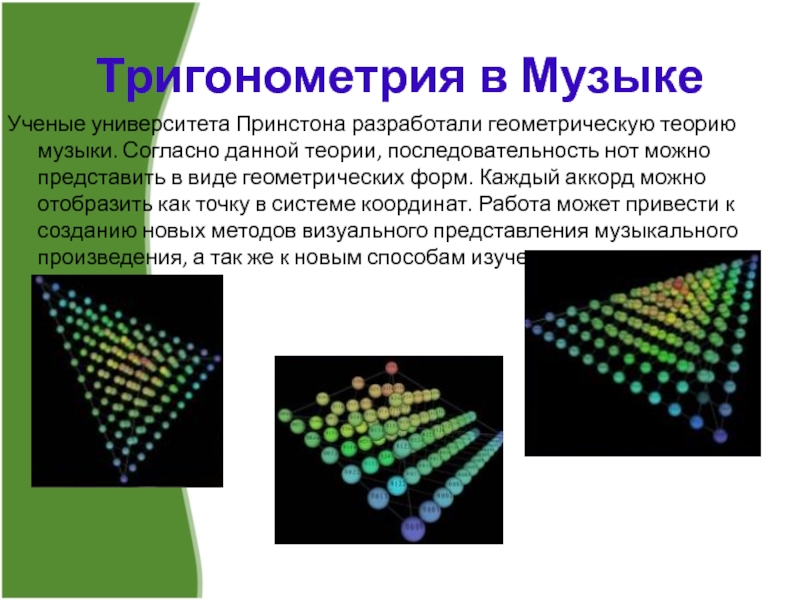
- 14. Тригонометрия в Музыке Ученые университета Принстона разработали
- 15. Тригонометрия в архитектуре Широко используется тригонометрия в
- 16. Вывод:Тригонометрия прошла длинный путь развития. И теперь,
- 17. СПАСИБО ЗА ВНИМАНИЕ!
- 18. Скачать презентанцию
Тема:Тригонометрия и ее применение в различных сферах науки и жизни.
Слайды и текст этой презентации
Слайд 1Проектная работа по алгебре
«Тригонометрия и ее применение в различных сферах
науки и жизни».
Пискун Елена Михайловна.Слайд 4Цель: Связь тригонометрии с реальной жизнью.
Задачи:
Изучить историю возникновения тригонометрии.
Узнать,
в каких сферах науки и искусства применяется тригонометрия.
Слайд 5 Гипотеза:
Тригонометрия применяется не только в алгебре и началах
анализа, но и во многих других науках, таких как биология,
архитектура, 3D графика и музыка.Слайд 6Тригонометрия- – (от греч. trigwnon – треугольник и metrew –
измеряю ), то есть измерение треугольников) – раздел математики в
котором изучается тригонометрические функции и их использование в геометрии.Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).