Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифракция
Содержание
- 1. Дифракция
- 2. Опыт Юнга с интерференцией от двух щелей
- 3. усиливающей интерференции (рис. 7.1). Такое предсказание казалось
- 4. источники, с которыми приходится иметь дело в
- 5. Рис. 7.2. Дифракция на мелкой монете (а)
- 6. 7.1. Принцип Гюйгенса-ФренеляДифракцией называется совокупность явлений наблюдаемых
- 7. Слайд 7
- 8. Принцип Гюйгенса, являясь чисто геометрическим способом построения
- 9. Слайд 9
- 10. Рис. 7.4
- 11. центром S). Френель разбил волновую поверхность Ф
- 12. Рис. 7.5
- 13. Слайд 13
- 14. (7.2.5)
- 15. Слайд 15
- 16. Френеля:
- 17. Зонная пластинка − перекрыты все четные зоны Френеля на волновой поверхности
- 18. КОНЕЦ ЛЕКЦИИЕЩЕ НЕ БЛИЗОК!!!НЕ ТОРМОЗИ, ФИЗИКОЙ ЗАРЯЖАЙ МОЗГИ!!!
- 19. Слайд 19
- 20. Рис. 7.6
- 21. Рис. 7.6
- 22. Дифракция на круглом отверстии и диске. В
- 23. Рис. 7.7
- 24. Слайд 24
- 25. Слайд 25
- 26. Скачать презентанцию
Опыт Юнга с интерференцией от двух щелей обеспечил прочную основу волновой теории света. Однако общее признание волновая теория получила лишь благодаря детальному изучению дифракции более чем через десятилетие.Мы уже бегло упоминали
Слайды и текст этой презентации
Слайд 1
Лекция 7
Тема: ДИФРАКЦИЯ
7.1. Принцип Гюйгенса-Френеля;
7.2.Метод зон Френеля;
7.3.Дифракция Френеля:
7.3.1. Дифракция
на круглом отверстии;
Слайд 2Опыт Юнга с интерференцией от двух щелей обеспечил прочную основу
волновой теории света. Однако общее признание волновая теория получила лишь
благодаря детальному изучению дифракции более чем через десятилетие.Мы уже бегло упоминали о дифракции при изучении волн на поверхности воды и в связи с обсуждением волновой природы света. Напомним, что под дифракцией понимают огибание волнами препятствий. Рассмотрим теперь дифракцию более подробно.
Определенный период в истории волновой теории света неразрывно связан с именем Огюстена Френеля (1788-1827). В 1819 г. он представил Парижской Академии наук волновую теорию света, которая предсказывала и объясняла явления интерференции и дифракции. Почти сразу же Симон Пуассон (1781-1840) обратил внимание на одно следствие теории Френеля, противоречащее интуитивным представлениям: согласно волновой теории Френеля, если свет от точечного источника падает на непрозрачный диск, то в результате дифракции на краях диска в центре тени должно возникать светлое пятно вследствие
Слайд 3усиливающей интерференции (рис. 7.1). Такое предсказание казалось весьма неправдоподобным. Но
когда предложенный Пуассоном эксперимент осуществил Франсуа Араго, в самом центре
тени он обнаружил светлое пятно! Это послужило убедительным доказательством справедливости волновой теории.На рис. 7.2, а представлена тень от монеты, освещаемой (почти) точечным источником (в данном случае лазером). В центре наблюдается светлое пятно. Обратите внимание на то, что за пределами тени наблюдаются светлые и темные полосы. Они напоминают интерференционные полосы при интерференции от двух щелей. Но в действительности эти полосы возникают при интерференции волн, которые дифрагируют на различных участках диска; вся картина носит название дифракционной. Подобная картина возникает при освещении точечным источником любого объекта с резкими краями, как показано на рис. 7.2,6 и в. Мы не всегда замечаем дифракционные картины, так как в большинстве случаев
Рис. 7.1
Слайд 4источники, с которыми приходится иметь дело в повседневной жизни, оказываются
не точечными и свет от различных участков таких источников смазывает
картину.Слайд 5
Рис. 7.2. Дифракция на мелкой монете (а) 1976 г.; на
лезвии бритвы (б) 1949 г., на одной щели, освещенной почти
точечным источником монохроматического света (в) 1962 г.
Слайд 67.1. Принцип Гюйгенса-Френеля
Дифракцией называется совокупность явлений наблюдаемых при распространении свет
в среде с резкими неоднородностями, размеры которых сравнимы с длинной
волны, и связанных с отклонениями от законов геометрической оптики.Огибание препятствий звуковыми волнами (дифракция звуковых волн) наблюдается нами постоянно (слышим звук за углом дома). Для наблюдения дифракции световых лучей нужны особые условия, это связано с малой длиной световых волн.
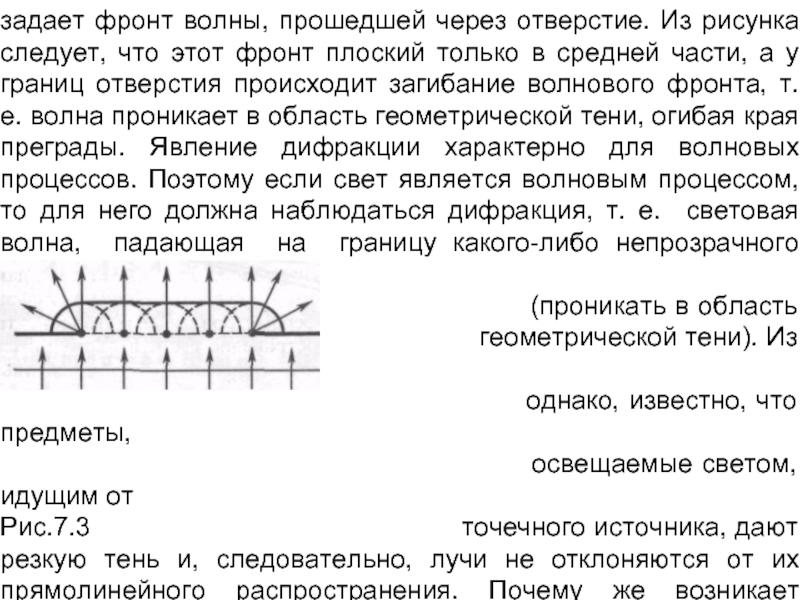
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. В качестве примера применения принципа Гюйгенса рассмотрим падение плоской волны на преграду с отверстием (рис. 7.3). Когда волновой фронт доходит до преграды, то каждая точка отверстия становится источником вторичных волн, а огибающая этих волн
Слайд 8Принцип Гюйгенса, являясь чисто геометрическим способом построения волновых поверхностей, решает
лишь задачу о направлении распространения волнового фронта, но не затрагивает
по существу вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить физически бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения
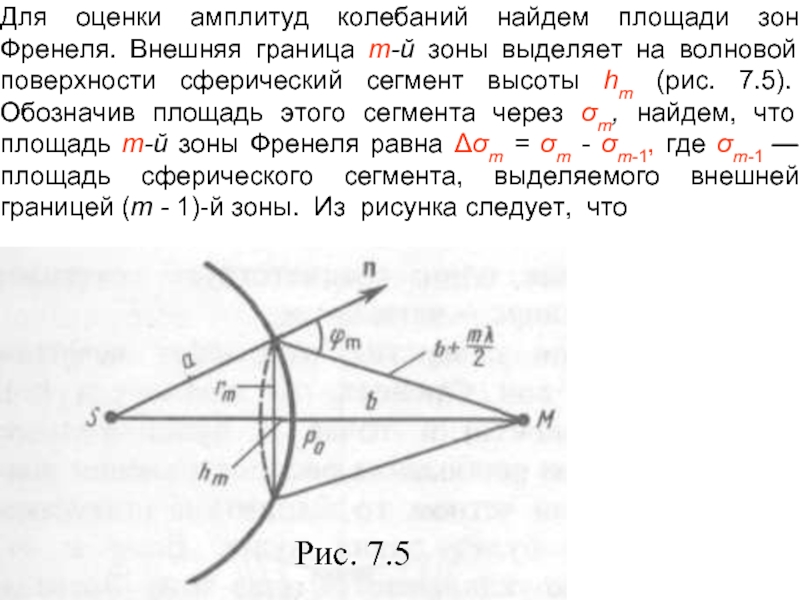
Слайд 11центром S). Френель разбил волновую поверхность Ф на кольцевые зоны
такого размера, чтобы расстояния от краев зоны до М отличались
на λ/2, т. е. P1M - Р0М = Р2М - Р1М = Р3М - Р2М = ... = λ/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусамиТак как колебания от соседних зон проходят до точки М расстояния, отличающиеся на λ/2, то в точку М они приходят с противоположными фазами и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке
A=Al - A2 + A3 – A4 + ...± Am, (7.2.1)
где А1 А2, ...,Аm — амплитуды колебаний, возбуждаемых 1-й, 2-й,..., m-й зонами.
Слайд 16Френеля:
(7.2.7)
При а = b = 10 см и λ = 0,5 мкм радиус первой (центральной) зоны r1 = 0,158 мм. Следовательно, распространение света от S к М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, т. е. прямолинейно. Таким образом, волновой принцип Гюйгенса — Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки — в простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, соединяющей эти две точки, то для света длины волны λ она перекроет четные зоны и оставит свободными нечетные начиная с центральной. В результате этого
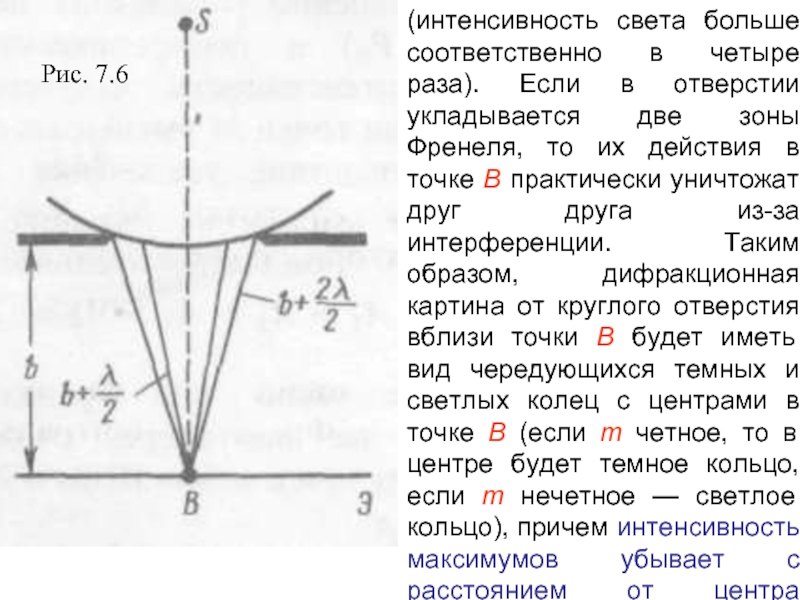
Слайд 22Дифракция на круглом отверстии и диске. В центре будет темное
пятно, если открыто четное число зон Френеля и светлое –
если нечетное.
Теги