Теорема Гаусса

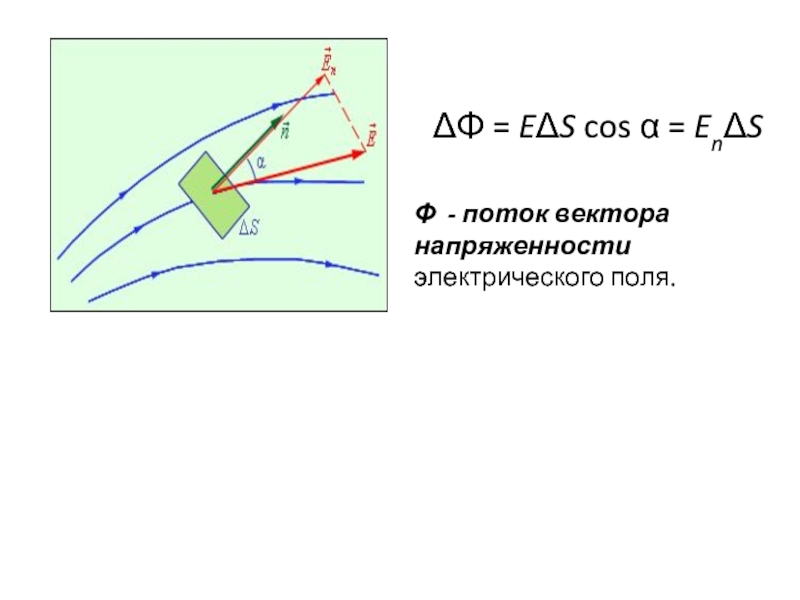
поверхность на малые площадки ΔSi, определить элементарные потоки

через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора

через замкнутую поверхность S

В случае замкнутой поверхности всегда выбирается внешняя нормаль.

поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной

электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает

задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R.
Эта задача имеет осевую симметрию. Из соображений симметрии, электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов

поверхность цилиндра, площадь которой равна 2πrl, так как поток через

Применение теоремы Гаусса дает:

где τ – заряд единицы длины цилиндра. Отсюда

целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих

где σ – поверхностная плотность заряда, то есть заряд, приходящийся на единицу площади.