Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение 9 класс
Содержание
- 1. Движение 9 класс
- 2. Движение-это жизнь.
- 3. Движение
- 4. Задачи урока.Закрепить понятие движения, виды движения.Отработать навыки
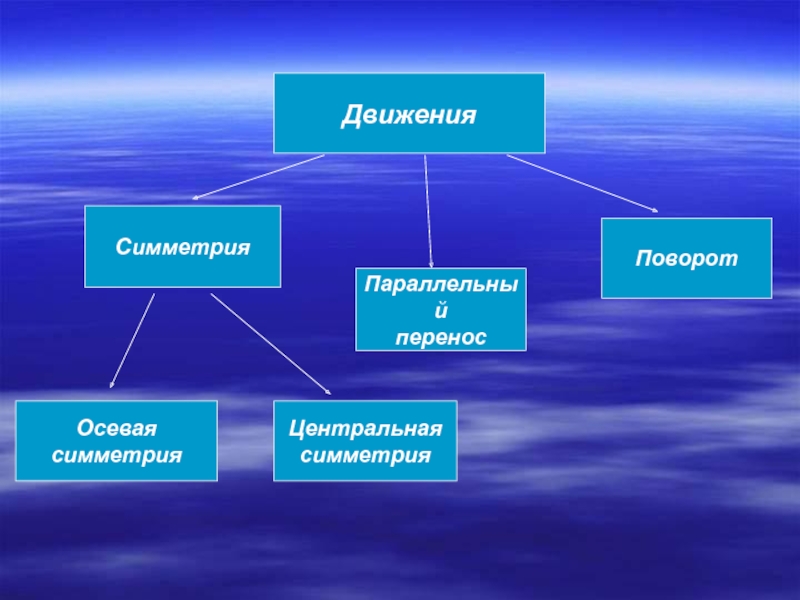
- 5. ДвиженияСимметрияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
- 6. Осевая симметрия Определение Осевая
- 7. ПостроениеПусть а – ось симметрии.
- 8. Слайд 8
- 9. Слайд 9
- 10. Задача Сколько осей симметрии имеет равносторонний
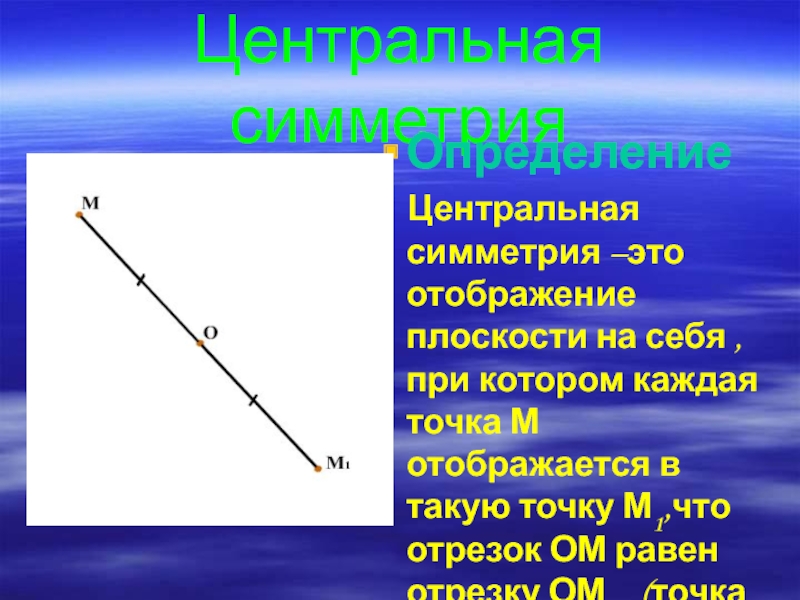
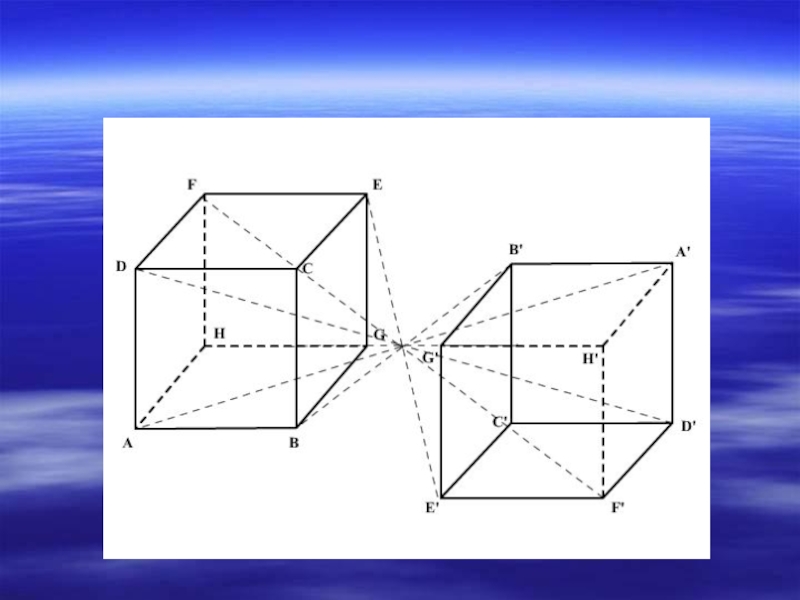
- 11. Центральная симметрияОпределение Центральная симметрия –это отображение
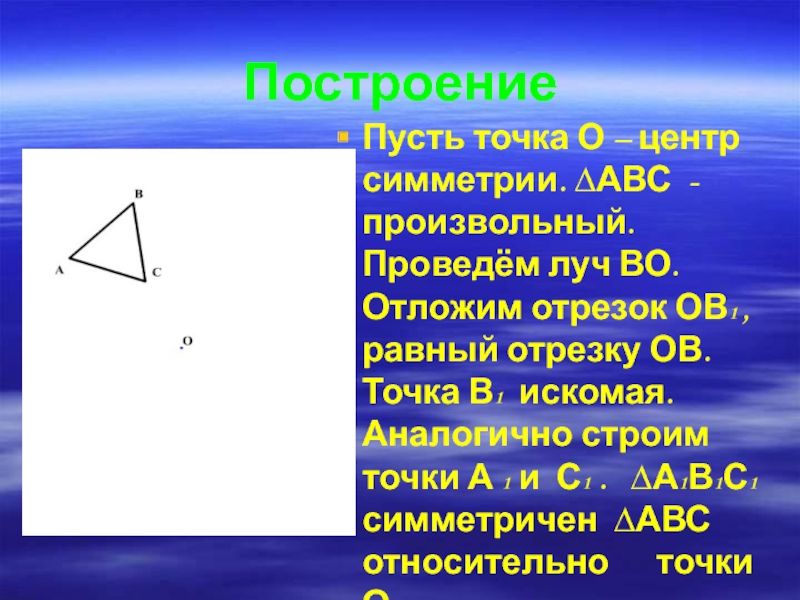
- 12. ПостроениеПусть точка О – центр симметрии. ∆АВС
- 13. Слайд 13
- 14. Слайд 14
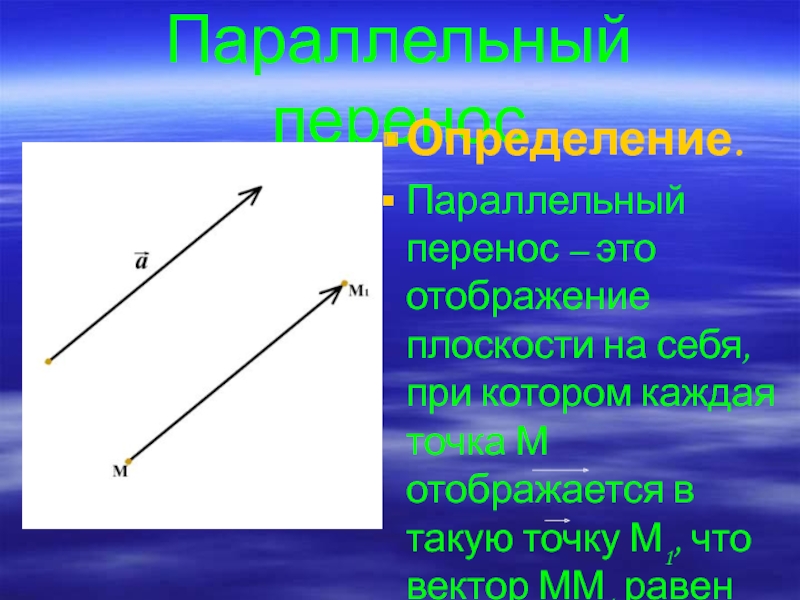
- 15. Параллельный переносОпределение. Параллельный перенос – это отображение
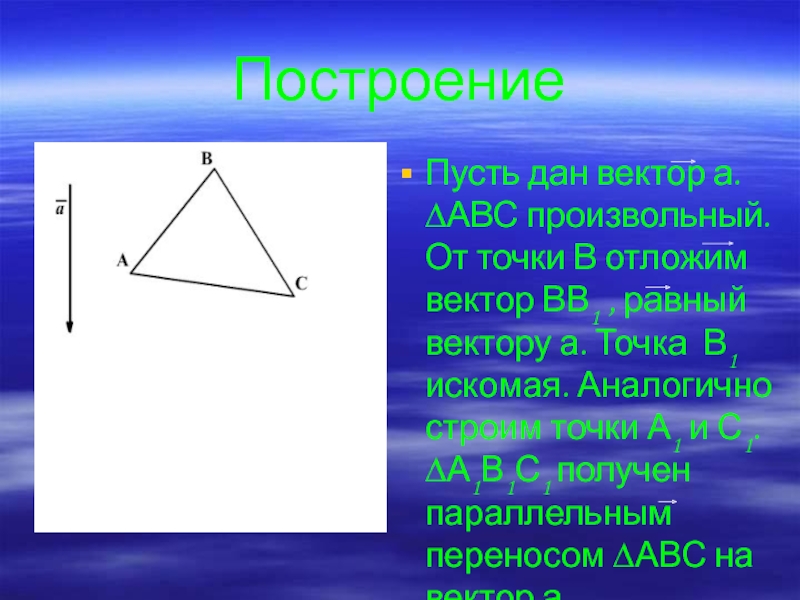
- 16. ПостроениеПусть дан вектор а. ∆АВС произвольный. От
- 17. Слайд 17
- 18. Слайд 18
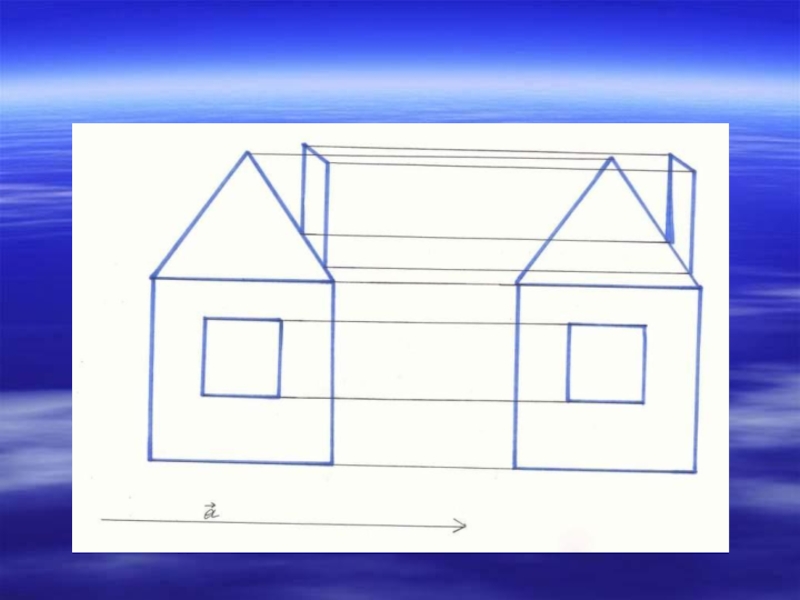
- 19. Движение в архитектуре. Определить вид движения.
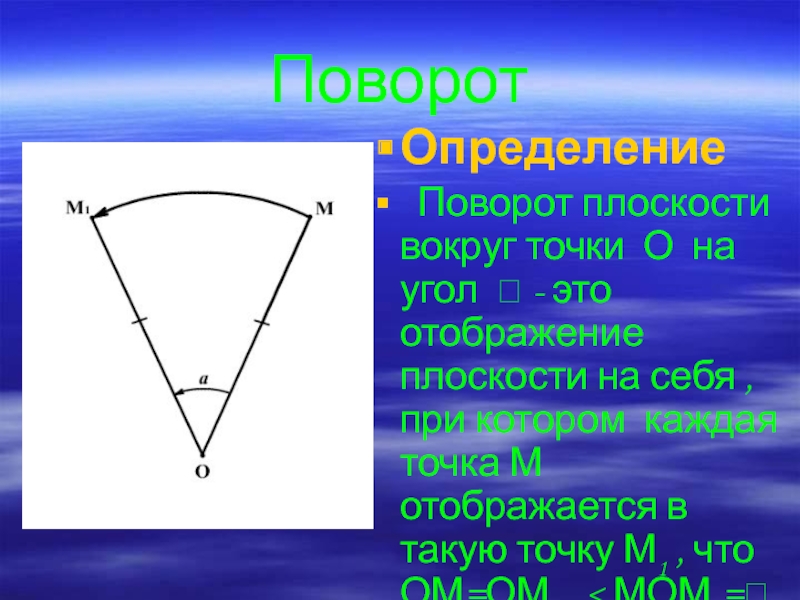
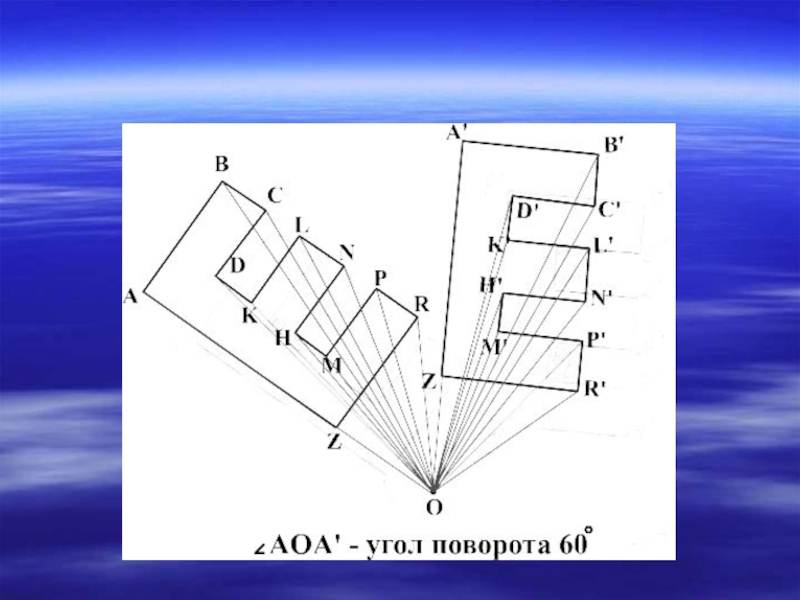
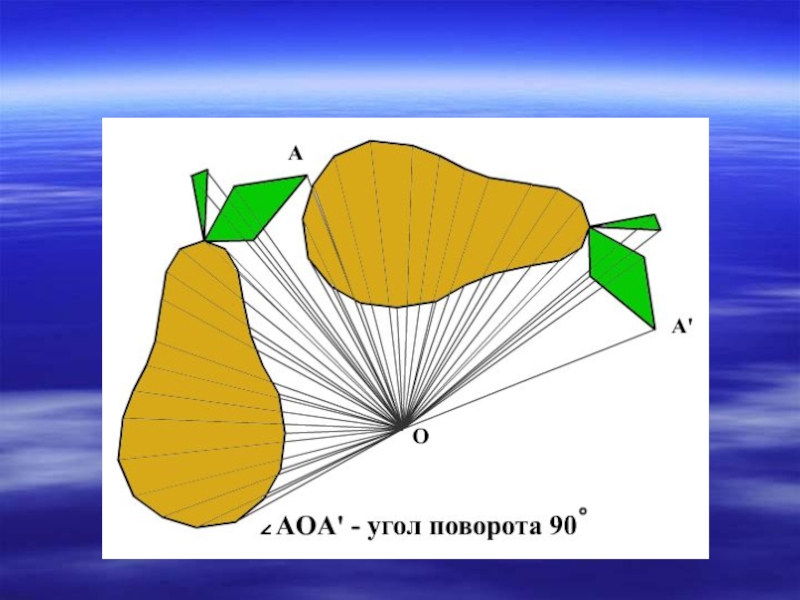
- 20. ПоворотОпределение Поворот плоскости вокруг точки
- 21. ПостроениеПусть О – центр поворота, =90º, ∆АВС
- 22. Слайд 22
- 23. Слайд 23
- 24. ВопросыОпределить вид симметрии.Что вам приходилось встречать в природе из известных видов симметрии?
- 25. Симметрия в природе
- 26. Слайд 26
- 27. Слайд 27
- 28. Симметрия в архитектуре
- 29. Слайд 29
- 30. Что происходит в алгебре?
- 31. Какие из данных графиков можно отнести к
- 32. Выполнение практической работыВыполни работу на тот вид движения, который тебе понравился.
- 33. Выбери себе задание: работа в парахС-11,
- 34. Какие
- 35. Скачать презентанцию
Движение-это жизнь.
Слайды и текст этой презентации
Слайд 4Задачи урока.
Закрепить понятие движения, виды движения.
Отработать навыки построения симметрии, параллельного
переноса, поворота.
Слайд 6Осевая симметрия
Определение
Осевая симметрия –это отображение
плоскости на себя, при котором каждая точка М отображается в
такую точку М1, что отрезок ММ1 перпендикулярен прямой а (оси симметрии ) и отрезок МР равен отрезку РМ1.
Слайд 7Построение
Пусть а – ось симметрии.
∆АВС – произвольный.
Проведем перпендикуляр ВР к прямой а. Отложим на прямой ВР
отрезок РВ1 , равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 10Задача
Сколько осей симметрии имеет равносторонний треугольник?
Сколько осей симметрии имеет квадрат? (2 ряд)
Сколько осей симметрии имеет ромб, не являющийся квадратом?
(вместе)
Начертите и убедитесь в правильности своего ответа
Слайд 11Центральная симметрия
Определение
Центральная симметрия –это отображение плоскости на себя
, при котором каждая точка М отображается в такую точку
М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
Слайд 12Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 , равный отрезку ОВ. Точка В1
искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
Слайд 15Параллельный перенос
Определение.
Параллельный перенос – это отображение плоскости на себя,
при котором каждая точка М отображается в такую точку М1,
что вектор ММ1 равен вектору а.
Слайд 16Построение
Пусть дан вектор а. ∆АВС произвольный. От точки В отложим
вектор ВВ1 , равный вектору а. Точка В1 искомая. Аналогично
строим точки А1 и С1. ∆А1В1С1 получен параллельным переносом ∆АВС на вектор а.
Слайд 20Поворот
Определение
Поворот плоскости вокруг точки О на угол
- это отображение плоскости на себя , при котором
каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 , < МОМ1=.
Слайд 21Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём
отрезок АВ, от него по часовой стрелке отложим
равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
Слайд 24Вопросы
Определить вид симметрии.
Что вам приходилось встречать в природе из известных
видов симметрии?
Слайд 33Выбери себе задание:
работа в парах
С-11, вар. Б1,2 - №1
С-12,
вар. А1,2 - №1
С-12, вар. Б1,2 - №2
Слайд 34
Какие виды движения мы
встречаем с вами в нашей повседневной жизни?
Привлекла ли вас красота симметрии, поворота и движения в архитектуре?
