Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические места точек
Содержание
- 1. Геометрические места точек
- 2. Упражнение 1
- 3. Упражнение 2На данной прямой a найдите точки,
- 4. На прямой c отметьте точки, удаленные от
- 5. Пересечение фигурПусть Ф1 и Ф2 – фигуры
- 6. Упражнение 4Даны две точки O1 и O2.
- 7. Объединение фигурПусть Ф1 и Ф2 – фигуры
- 8. Упражнение 5Даны две точки O1 и O2.
- 9. Разность фигурПусть Ф1 и Ф2 – фигуры
- 10. Упражнение 6Даны две точки O1 и O2.
- 11. Серединный перпендикулярСерединным перпендикуляром к заданному отрезку называется
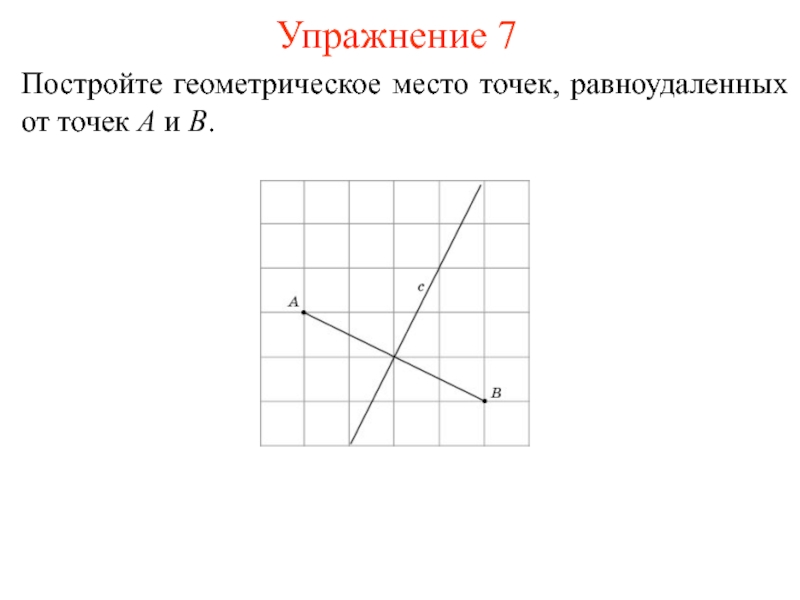
- 12. Упражнение 7Постройте геометрическое место точек, равноудаленных от точек A и B.
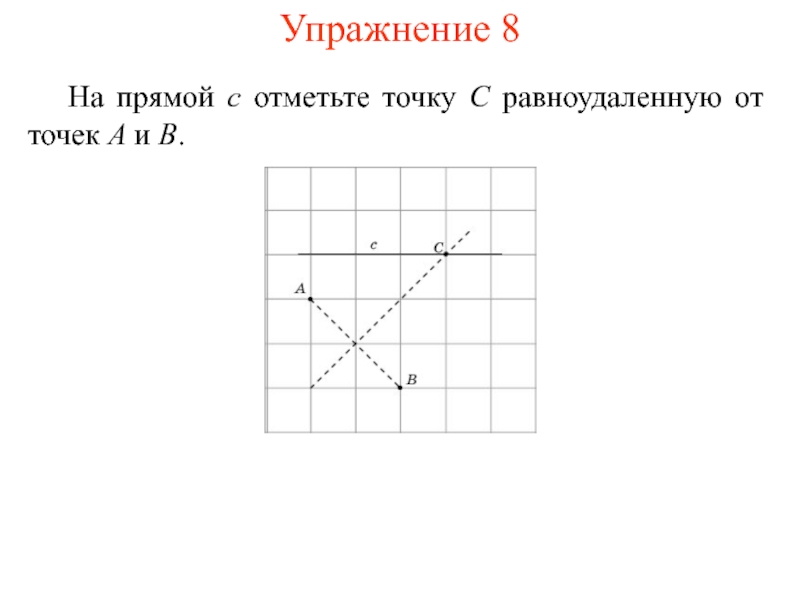
- 13. На прямой c отметьте точку C равноудаленную от точек A и B. Упражнение 8
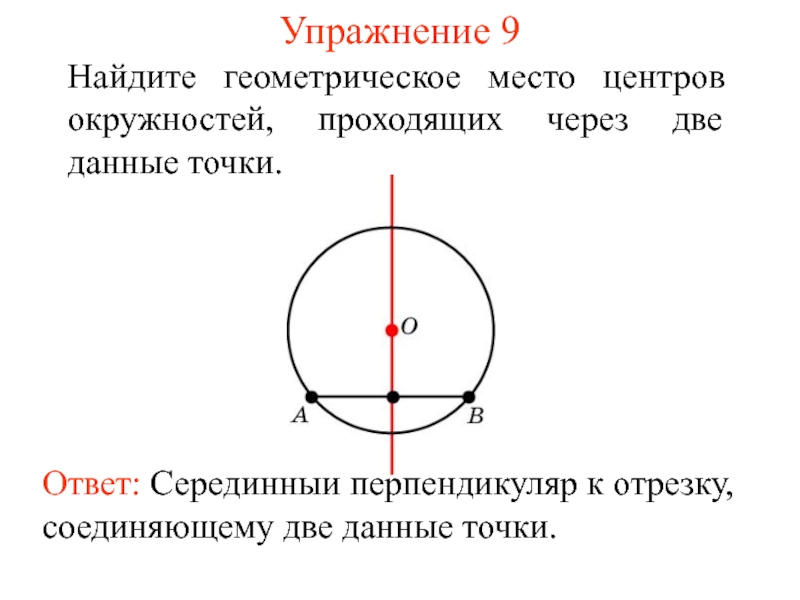
- 14. Упражнение 9Найдите геометрическое место центров окружностей, проходящих через две данные точки.
- 15. Упражнение 10Найдите геометрическое место вершин С равнобедренных треугольников с заданным основанием AB.
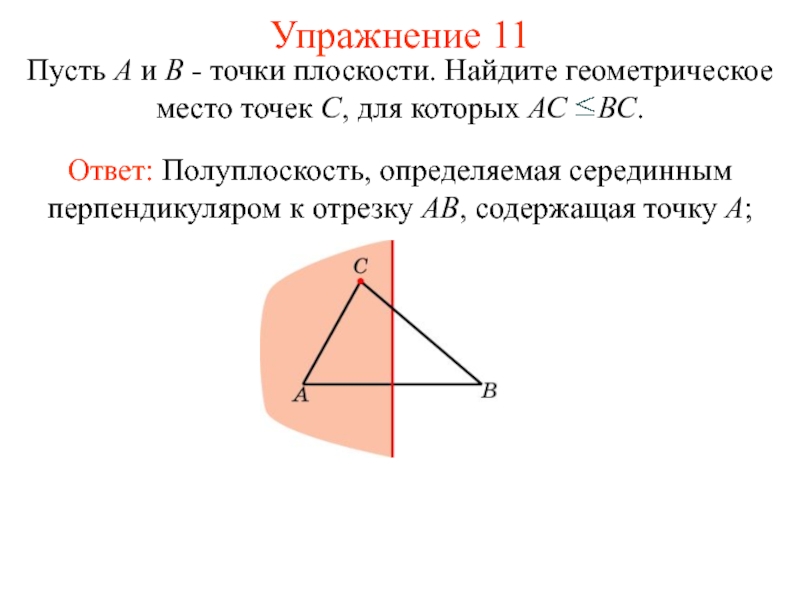
- 16. Упражнение 11Пусть А и В - точки
- 17. Упражнение 12Пусть А и В точки плоскости,
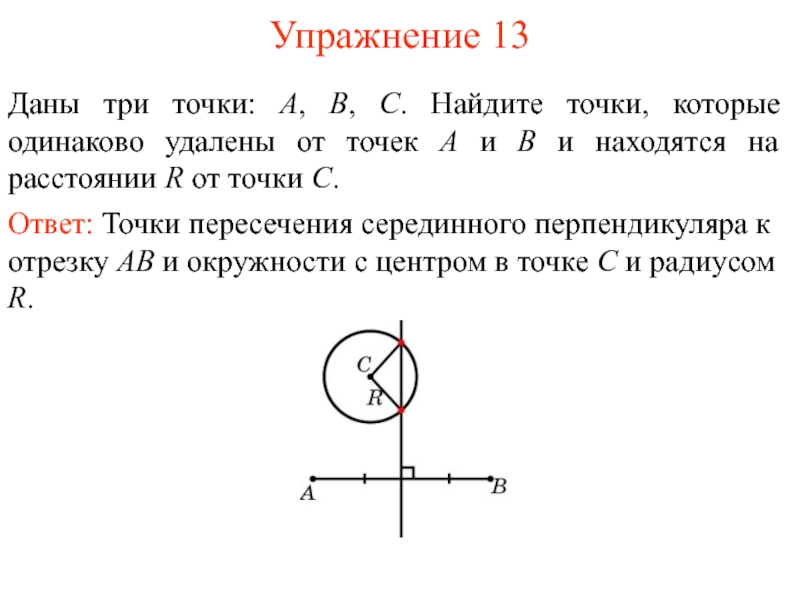
- 18. Упражнение 13Даны три точки: А, В, С.
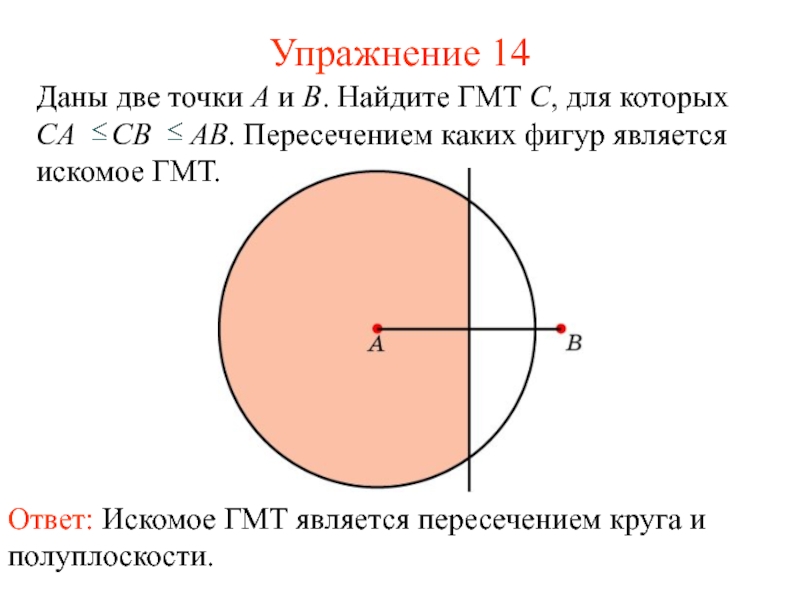
- 19. Упражнение 14
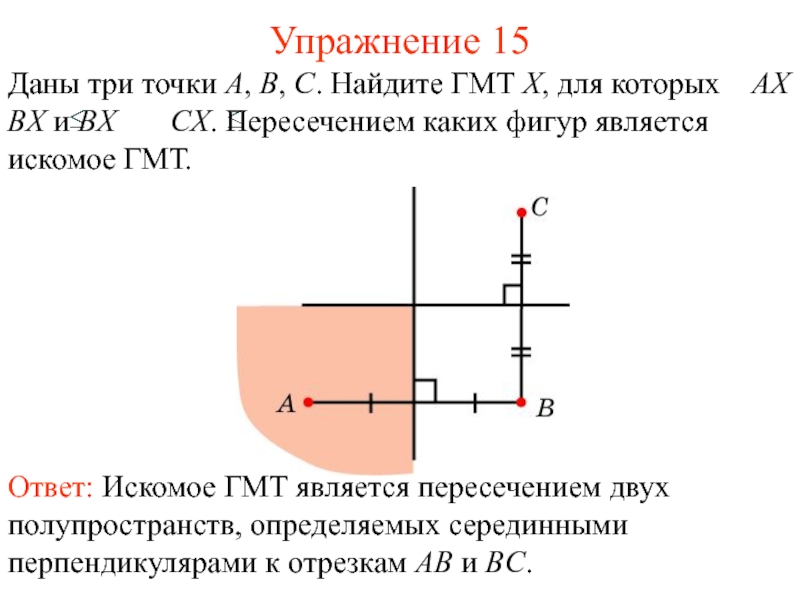
- 20. Упражнение 15Даны три точки A, B, C.
- 21. Упражнение 16Даны три точки A, B, C.
- 22. Биссектриса углаТеорема. Биссектриса угла является ГМТ, лежащих
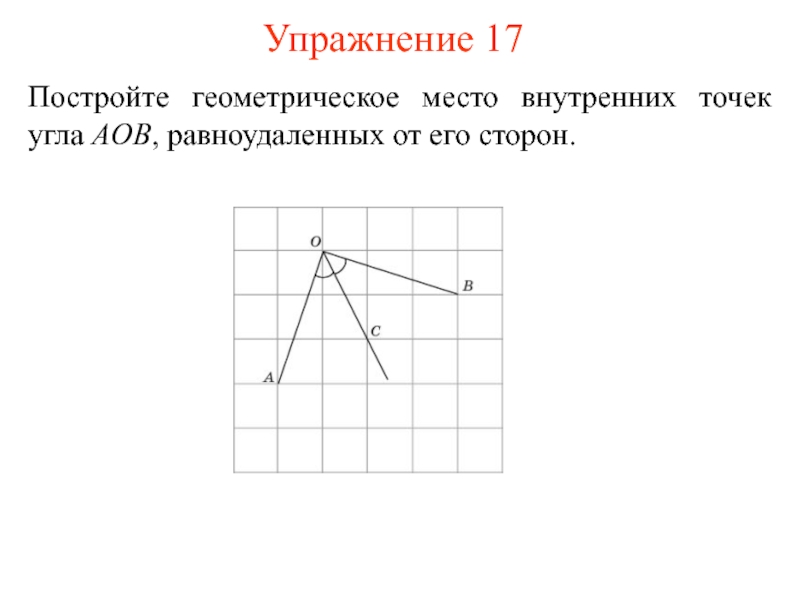
- 23. Постройте геометрическое место внутренних точек угла AOB, равноудаленных от его сторон. Упражнение 17
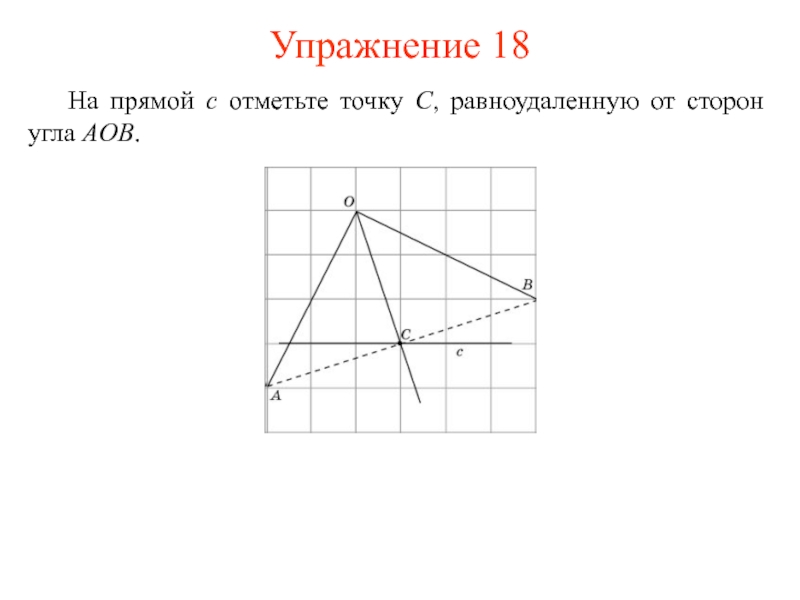
- 24. На прямой c отметьте точку C, равноудаленную от сторон угла AOB. Упражнение 18
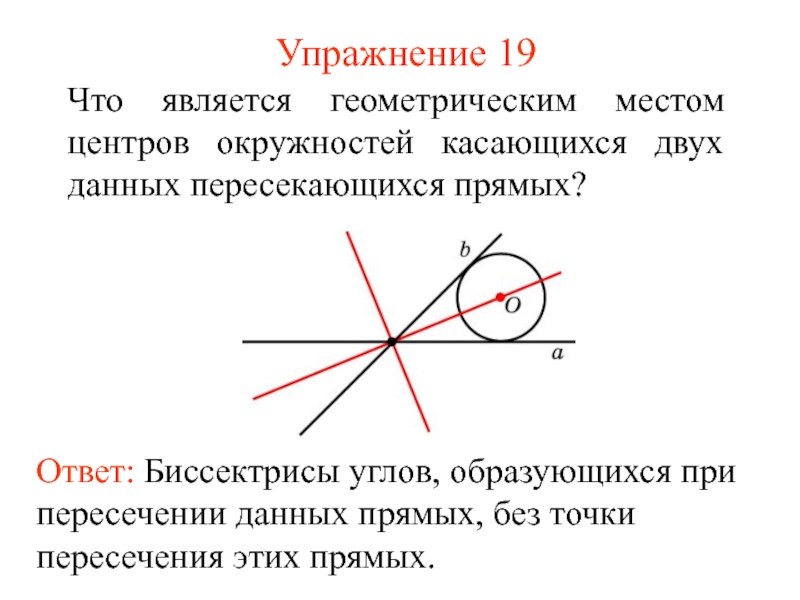
- 25. Упражнение 19Что является геометрическим местом центров окружностей касающихся двух данных пересекающихся прямых?
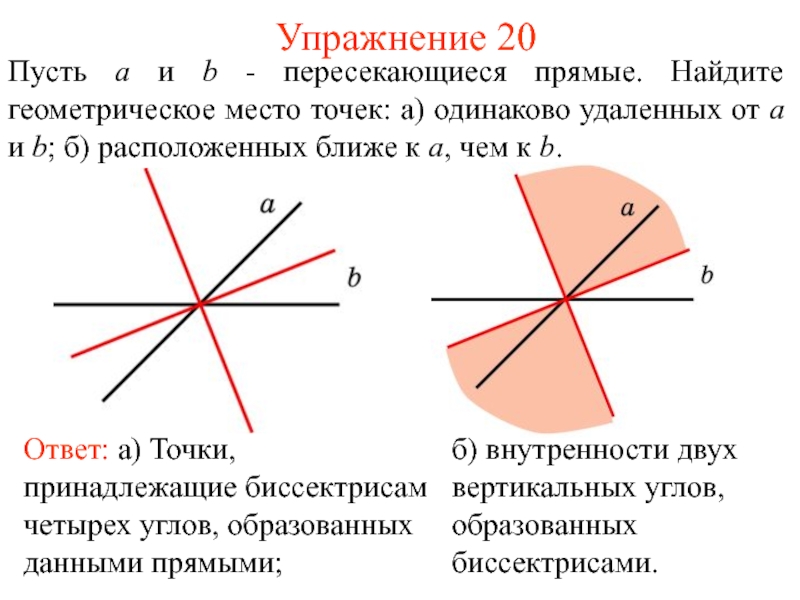
- 26. Упражнение 20Пусть a и b - пересекающиеся
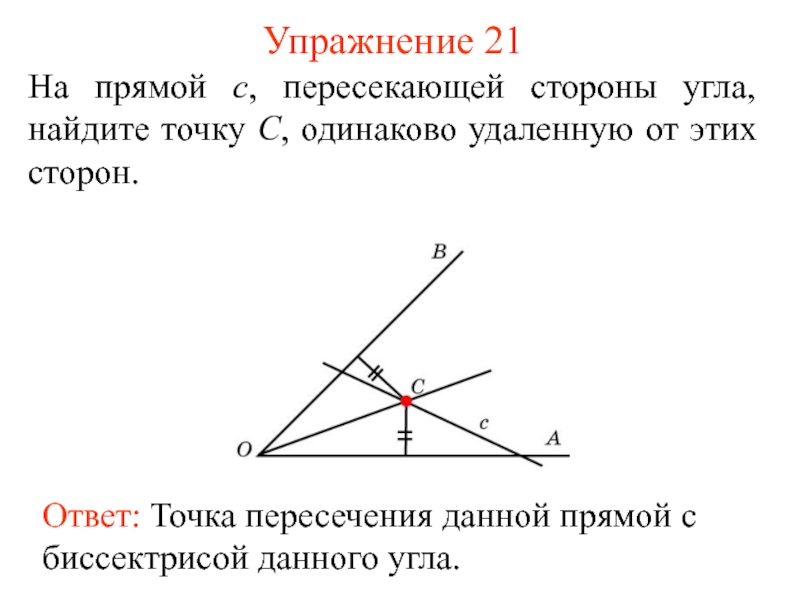
- 27. Упражнение 21На прямой c, пересекающей стороны угла, найдите точку C, одинаково удаленную от этих сторон.
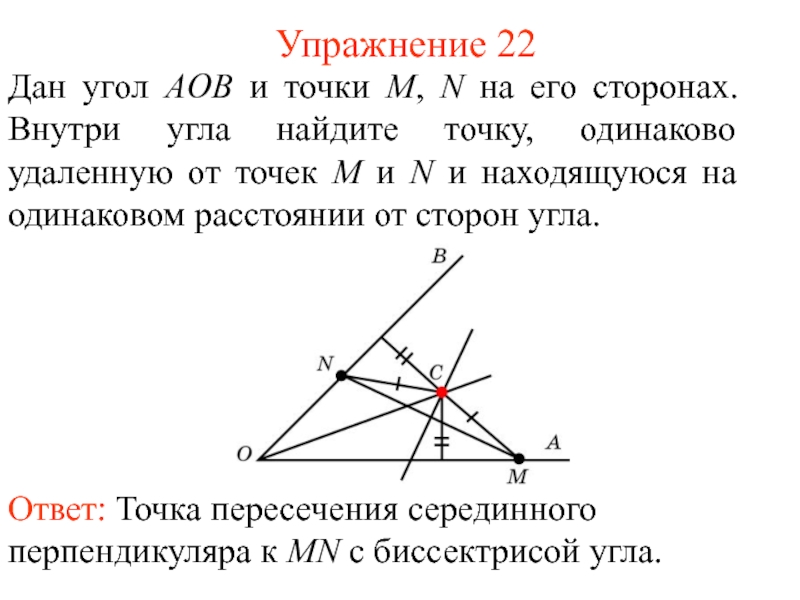
- 28. Упражнение 22Дан угол АOB и точки M,
- 29. Скачать презентанцию
Упражнение 1
Слайды и текст этой презентации
Слайд 1Геометрические места точек
Геометрическим местом точек (ГМТ) называется фигура,
состоящая из всех точек, удовлетворяющих заданному свойству или нескольким заданным свойствам.
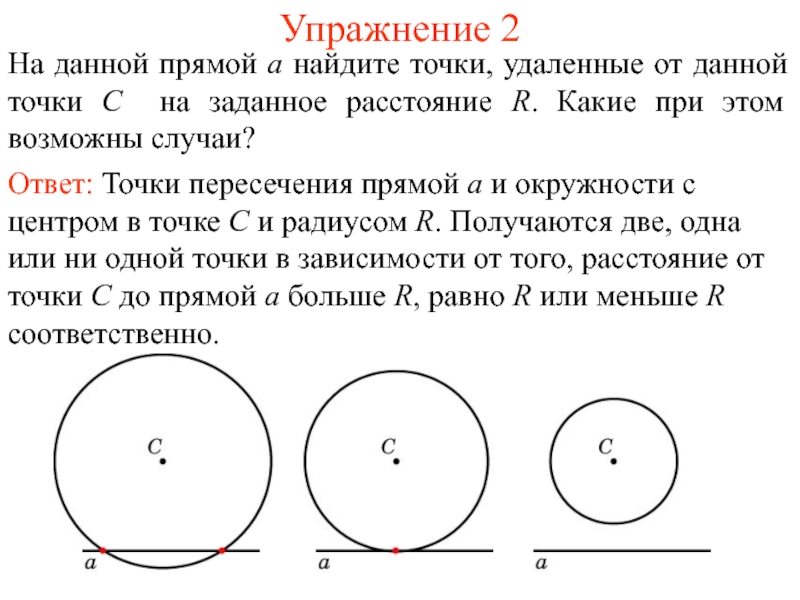
Слайд 3Упражнение 2
На данной прямой a найдите точки, удаленные от данной
точки C на заданное расстояние R. Какие при этом возможны
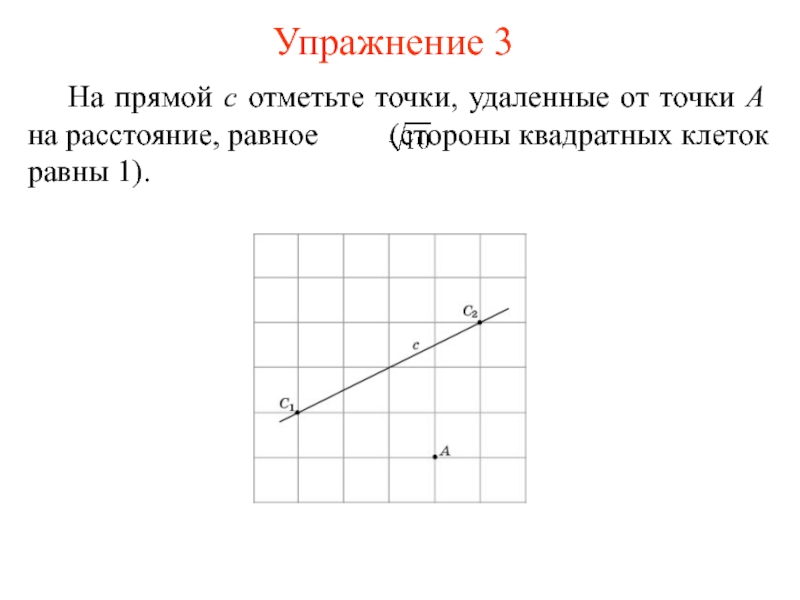
случаи?
Слайд 4 На прямой c отметьте точки, удаленные от точки A на
расстояние, равное (стороны квадратных клеток равны
1).Упражнение 3
Слайд 5Пересечение фигур
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура
Ф, состоящая из всех точек, принадлежащих фигуре Ф1 и фигуре
Ф2, называется пересечением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.
Слайд 6Упражнение 4
Даны две точки O1 и O2. Найдите ГМТ X,
для которых XO1
R1 и XO2 R2. Пересечением каких фигур является искомое ГМТ.
Слайд 7Объединение фигур
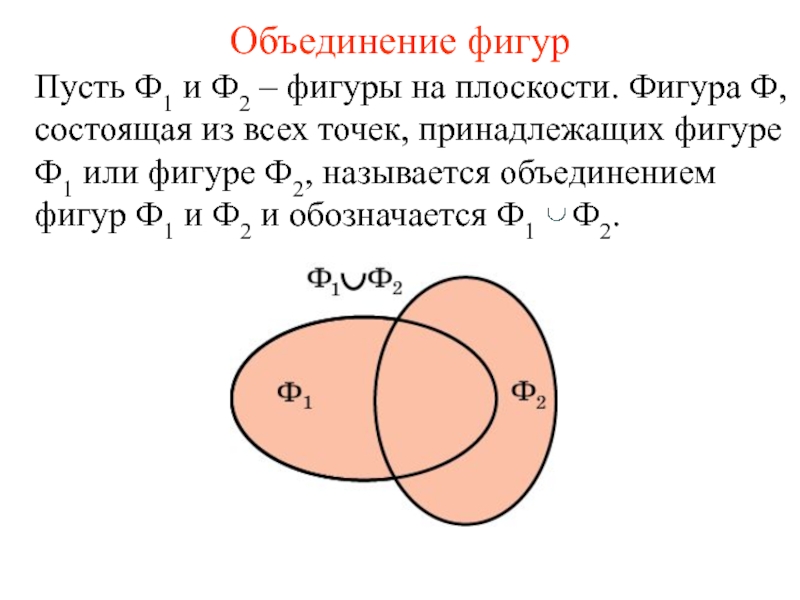
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура
Ф, состоящая из всех точек, принадлежащих фигуре Ф1 или фигуре
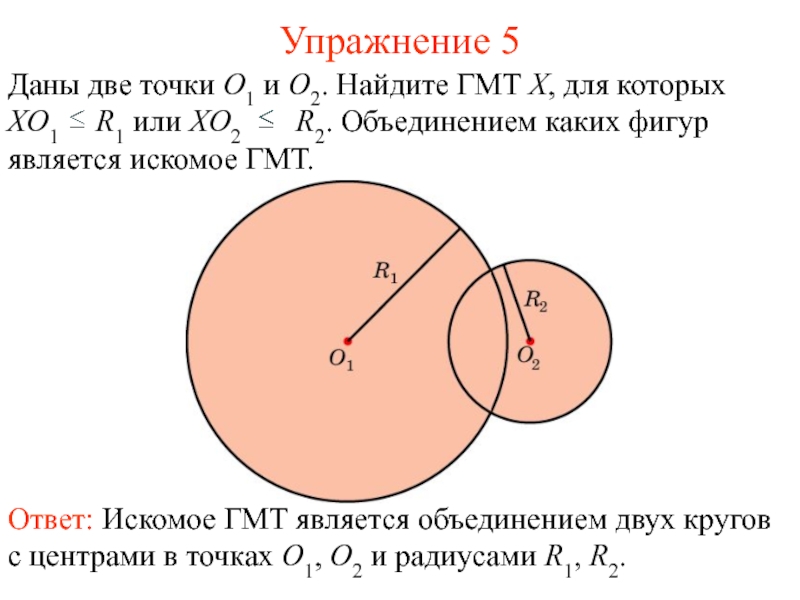
Ф2, называется объединением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.
Слайд 8Упражнение 5
Даны две точки O1 и O2. Найдите ГМТ X,
для которых XO1
R1 или XO2 R2. Объединением каких фигур является искомое ГМТ.
Слайд 9Разность фигур
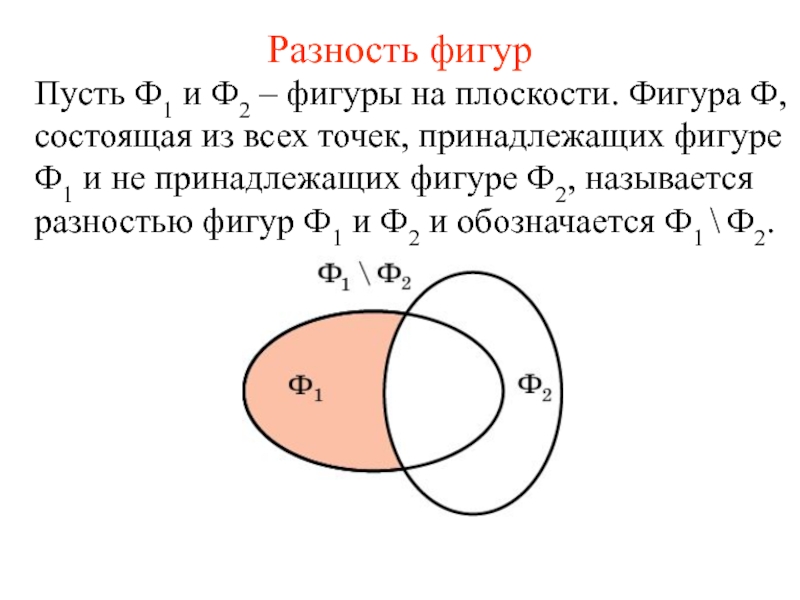
Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура
Ф, состоящая из всех точек, принадлежащих фигуре Ф1 и не
принадлежащих фигуре Ф2, называется разностью фигур Ф1 и Ф2 и обозначается Ф1 \ Ф2.
Слайд 10Упражнение 6
Даны две точки O1 и O2. Найдите ГМТ X,
для которых XO1
R1 и XO2 R2. Разностью каких фигур является искомое ГМТ.
Слайд 11Серединный перпендикуляр
Серединным перпендикуляром к заданному отрезку называется …
Теорема. Серединный перпендикуляр
к отрезку является ГМТ, одинаково удаленных от концов этого отрезка.
Доказательство. Пусть дан отрезок АВ и точка О – его середина. Очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру. Пусть точка С одинаково удалена от точек А и В и не совпадает с точкой О.
Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Тогда треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру.
Слайд 14Упражнение 9
Найдите геометрическое место центров окружностей, проходящих через две данные
точки.
Слайд 15Упражнение 10
Найдите геометрическое место вершин С равнобедренных треугольников с заданным
основанием AB.
Слайд 16Упражнение 11
Пусть А и В - точки плоскости. Найдите геометрическое
место точек С, для которых АС ВС.
Слайд 17Упражнение 12
Пусть А и В точки плоскости, c - прямая.
Найдите геометрическое место точек прямой c, расположенных ближе к А,
чем к В. В каком случае таких точек нет?
Слайд 18Упражнение 13
Даны три точки: А, В, С. Найдите точки, которые
одинаково удалены от точек А и В и находятся на
расстоянии R от точки С.
Слайд 20Упражнение 15
Даны три точки A, B, C. Найдите ГМТ X,
для которых AX BX и BX
CX. Пересечением каких фигур является искомое ГМТ.
Слайд 21Упражнение 16
Даны три точки A, B, C. Найдите ГМТ X,
для которых AX BX или BX
CX. Объединением каких фигур является искомое ГМТ.
Слайд 22Биссектриса угла
Теорема. Биссектриса угла является ГМТ, лежащих внутри этого угла
и одинаково удаленных от его сторон.
Доказательство. Рассмотрим угол c вершиной
в точке О и сторонами а, b. Пусть точка С лежит внутри данного угла. Опустим из нее перпендикуляры СА и CB на стороны а и b. Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и катету). Следовательно, углы AOC и BOC равны. Значит, точка C принадлежит биссектрисе угла. Обратно, если точка C принадлежит биссектрисе угла, то прямоугольные треугольники AOC и BOC равны (по гипотенузе и острому углу). Следовательно, AC = BC. Значит, точка С одинаково удалена от сторон данного угла. 
Слайд 23
Постройте геометрическое место внутренних точек угла AOB, равноудаленных от его
сторон.
Упражнение 17
Слайд 25Упражнение 19
Что является геометрическим местом центров окружностей касающихся двух данных
пересекающихся прямых?
Слайд 26Упражнение 20
Пусть a и b - пересекающиеся прямые. Найдите геометрическое
место точек: а) одинаково удаленных от a и b; б)
расположенных ближе к a, чем к b.
Слайд 27Упражнение 21
На прямой c, пересекающей стороны угла, найдите точку C,
одинаково удаленную от этих сторон.
Слайд 28Упражнение 22
Дан угол АOB и точки M, N на его
сторонах. Внутри угла найдите точку, одинаково удаленную от точек M
и N и находящуюся на одинаковом расстоянии от сторон угла.
