Координаты в пространстве 10-11 класс

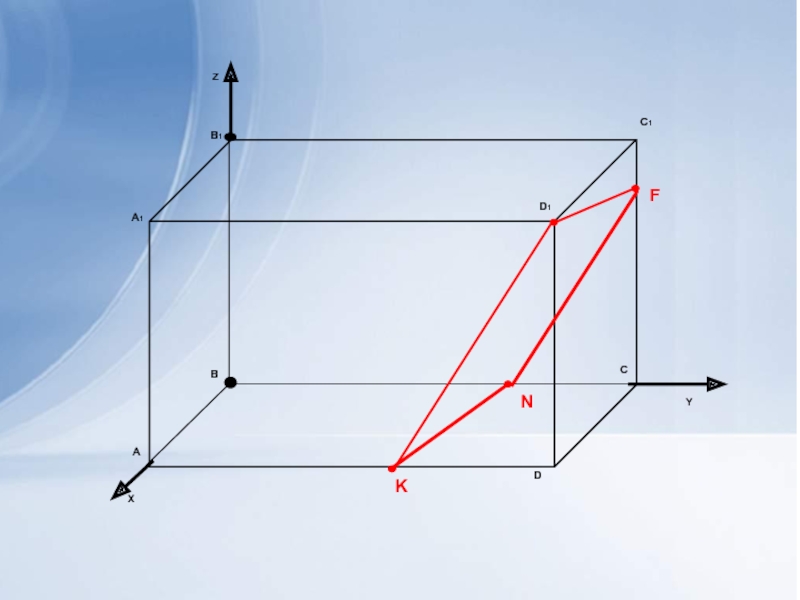
пространстве с помощью метода координат, используя учебные конспекты и справочные

Через решение на нахождение расстояний и углов в пространстве двумя способами (геометрическим и методом координат) сделать вывод о преимуществе второго для ряда задач этого блока.

Расширить представление о применении метода координат в решении стереометрических задач на построение сечений.

B2, P, Q – середины ребер. На диагонали А1С1взята точка

Введем систему координат.
За единицу измерения примем ребро куба а.

Найдем координаты нужных точек:
А(а; 0; 0), С(0; а; 0), B1(0; 0; а), C1(0; а; а),
B(0; 0; 0), D(а; а; 0), А1(а; 0; а)

По формулам координат середины отрезка или деления отрезка в данном отношении находим О1(а/2; а/2; а), P(а; а/2; 0),
R1(а/4; 3а/4; а), B2(0; 0; а/2),
F(3а/8; 7а/8; а/2), Q(а/2; а; 0).

Находим длину отрезка как расстояние между двумя точками по соответствующей формуле.

систему координат.
За единицу измерения примем ребро куба 1.

Найдем координаты

Найдем расстояние от точки до плоскости по формуле

точки А до плоскости α

Расстояние от
точки M до прямой

Расстояние между двумя
скрещивающимися
прямыми а и в

Расстояние
между параллельными
плоскостями α и β

а
и плоскостью α

Угол между
плоскостями α и β

0; 0), C(0;3;0), D(1;3;0), A1(1;0;2), B2(0;0;2), C1(0;3;2), D1(1;3;0).
В прямоугольном параллелепипеде

Для построения сечения найдем координаты
Найдем координаты еще двух точек М и К,
для чего:
а) Напишем уравнение искомой плоскости сечения α по вектору нормали и точке D1.

б) Найдем точки пересечения α с осями координат и некоторыми ребрами куба.
α∩OY=N, N(0; YN; 0); 3YN-6=0, YN=2,
N(0;2;0)
α∩AD=K, K(1; YК; 0); 1+3YK-6=0, YK=5/3,
K(1;5/3;0)

По точкам строим искомое сечение KD1FN