Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Окружность. Определения. Теоремы и следствия из теорем 9-11 класс
Содержание
- 1. Окружность. Определения. Теоремы и следствия из теорем 9-11 класс
- 2. Отрезки и прямые, связанные с окружностью.Окружность –
- 3. Прямая, пересекающая окружность в двух точках, называется
- 4. Свойства хорд и дуг окружности.Диаметр, перпендикулярный к
- 5. Диаметр, перпендикулярный к хорде, делит эту хорду
- 6. Диаметр, проходящий через середину хорды, перпендикулярен к
- 7. Если хорды равны, то они находятся на
- 8. Свойства хорд и дуг окружности.У равных дуг
- 9. Свойство хордПроизведение отрезков, на которые делятся хорды
- 10. Произведение отрезков, на которые делятся хорды точкой
- 11. Свойство касательныхЕсли к окружности из одной точки
- 12. Если к окружности из одной точки проведены
- 13. Касательная и секущаяДля касательной и секущей, проведённых
- 14. Для касательной и секущей, проведённых к одной
- 15. СекущиеДля двух секущих, проведённых из одной точки
- 16. Для двух секущих, проведённых из одной точки
- 17. Центральные и вписанные углы.Угол с вершиной в
- 18. Вписанные углы.Вписанный угол, опирающийся на полуокружность
- 19. Угол между касательной и хордой,
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Отрезки и прямые, связанные с окружностью.
Окружность – геометрическая фигура, состоящая
из всех точек плоскости, расположенный на заданном расстоянии от данной
точки (центра окружности)Точка О – центр окружности.
Отрезок , соединяющий центр окружности
с произвольной точкой окружности,
называется радиусом.
ОА – радиус окружности.
Отрезок, соединяющий две любые точки
окружности, называется хордой.
ВС – хорда окружности.
Самая длинная хорда проходит через центр окружности и называется диаметром окружности.
Диаметр окружности равен длине двух радиусов.
EF – диаметр окружности
E
F
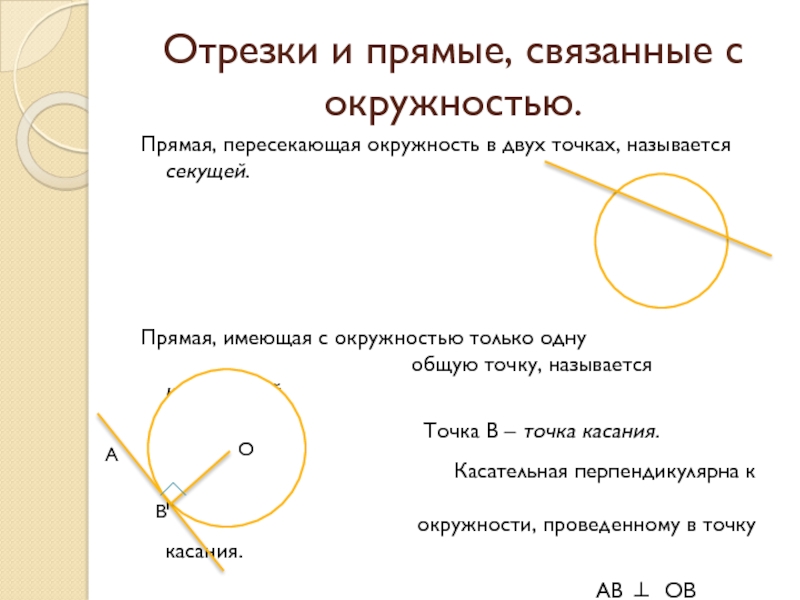
Слайд 3Прямая, пересекающая окружность в двух точках, называется секущей.
Прямая, имеющая с
окружностью только одну
общую точку, называется касательной.Точка В – точка касания.
Касательная перпендикулярна к радиусу
окружности, проведенному в точку касания.
АВ ОВ
Отрезки и прямые, связанные с окружностью.
Слайд 4Свойства хорд и дуг окружности.
Диаметр, перпендикулярный к хорде, делит эту
хорду и стягиваемые ею две дуги пополам. (см. доказательство)
АВ
– хорда, CD – диаметр.AB CD = E
, AC = CB
AD = DB
Справедливо и обратное утверждение:
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
(см. доказательство)
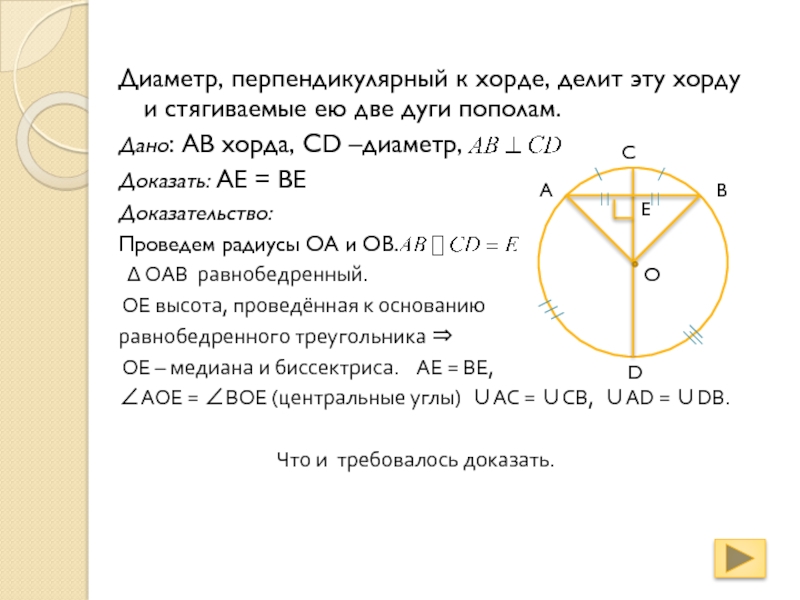
Слайд 5Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею
две дуги пополам.
Дано: АВ хорда, СD –диаметр,
Доказать: АЕ
= ВЕДоказательство:
Проведем радиусы ОА и ОВ.
OAB равнобедренный.
ОЕ высота, проведённая к основанию
равнобедренного треугольника
ОЕ – медиана и биссектриса. АЕ = ВЕ,
АОЕ = ВОЕ (центральные углы) АС = СВ, АD = DВ.
Что и требовалось доказать.
Слайд 6Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и
делит стягиваемые ею две дуги пополам.
Дано: АВ хорда, СD
–диаметр,АЕ = ВЕ
Доказать:
Доказательство:
Проведем радиусы ОА и ОВ.
OAB равнобедренный.
ОЕ медиана, проведённая к основанию
равнобедренного треугольника
ОЕ – высота и биссектриса. ОЕ АВ.
АОЕ = ВОЕ (центральные углы) АС = СВ, АD = DВ.
Что и требовалось доказать.
Слайд 7Если хорды равны, то они находятся на одном и том
же расстоянии от центра окружности.
AB = CDOF AB OF = OE
OE CD
Если хорды равноудалены
(находятся на одном и том же
расстоянии) от центра окружности, то они равны.
OF = OE
OF AB AB = CD
OE CD
Свойства хорд и дуг окружности.
Слайд 8Свойства хорд и дуг окружности.
У равных дуг равны и хорды.
AB = CD AB = CD
Дуги, заключённые между
параллельными хордами,
равны.
AB CD AD = BC
Слайд 9Свойство хорд
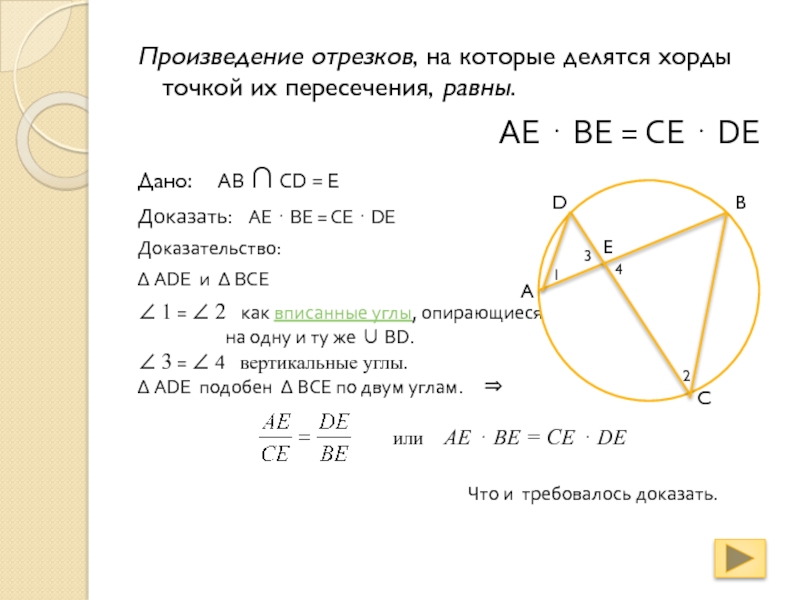
Произведение отрезков, на которые делятся хорды точкой их пересечения,
равны.
AE BE = CE DE
(см. доказательство)Слайд 10Произведение отрезков, на которые делятся хорды точкой их пересечения, равны.
Дано: AB CD = E
Доказать: AE BE = CE DE
Доказательство:
ADE и BCE
1 = 2 как вписанные углы, опирающиеся
на одну и ту же BD.
3 = 4 вертикальные углы.
ADE подобен BCE по двум углам.
или AE BE = CE DE
Что и требовалось доказать.
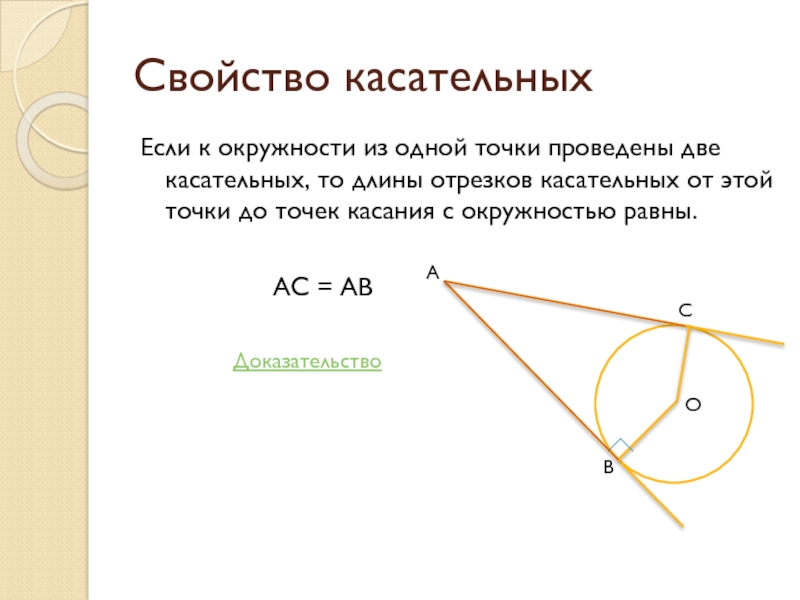
Слайд 11Свойство касательных
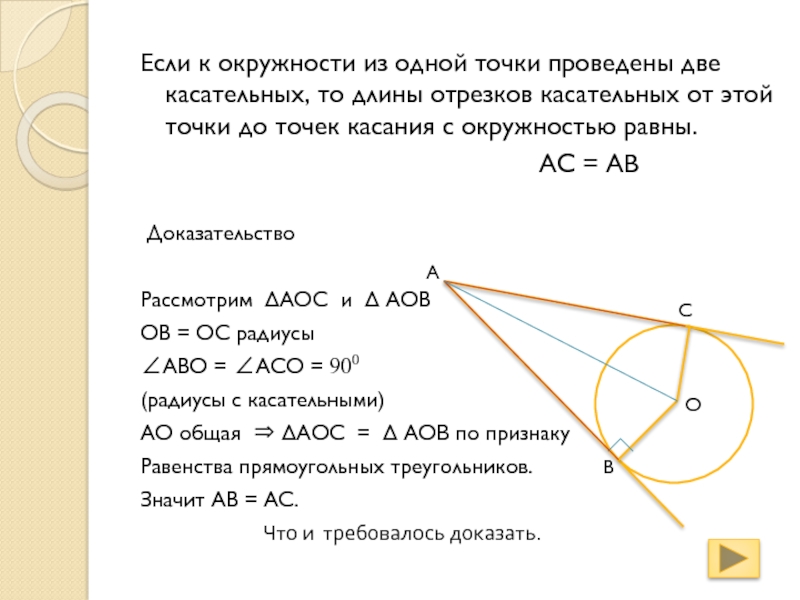
Если к окружности из одной точки проведены две касательных,
то длины отрезков касательных от этой точки до точек касания
с окружностью равны.АС = АВ
Доказательство
Слайд 12Если к окружности из одной точки проведены две касательных, то
длины отрезков касательных от этой точки до точек касания с
окружностью равны.АС = АВ
Доказательство
Рассмотрим АОС и АОВ
ОВ = ОС радиусы
АВО = АСО = 900
(радиусы с касательными)
АО общая АОС = АОВ по признаку
Равенства прямоугольных треугольников.
Значит АВ = АС.
Что и требовалось доказать.
Слайд 13Касательная и секущая
Для касательной и секущей, проведённых к одной окружности
из одной точки, справедливо равенство:
AB2= AD ACДоказательство
Слайд 14Для касательной и секущей, проведённых к одной окружности из одной
точки, справедливо равенство:
AB2= AD
ACДоказательство:
Проведём хорды ВС и BD. ABC и ABD подобны по двум углам.
А – общий, ABC = ADB
а значит
AB2= AD AC
Что и требовалось доказать.
Слайд 15Секущие
Для двух секущих, проведённых из одной точки вне круга, справедливо
равенство: AD AC = AF AE
Доказательство:
Слайд 16Для двух секущих, проведённых из одной точки вне круга, справедливо
равенство: AD AC = AF AE
Что и требовалось доказать.
Доказательство:
Проведём из точки А касательную АВ к окружности.
Тогда AB2= AD AC и AB2= AF AE
AD AC = AF AE
Слайд 17Центральные и вписанные углы.
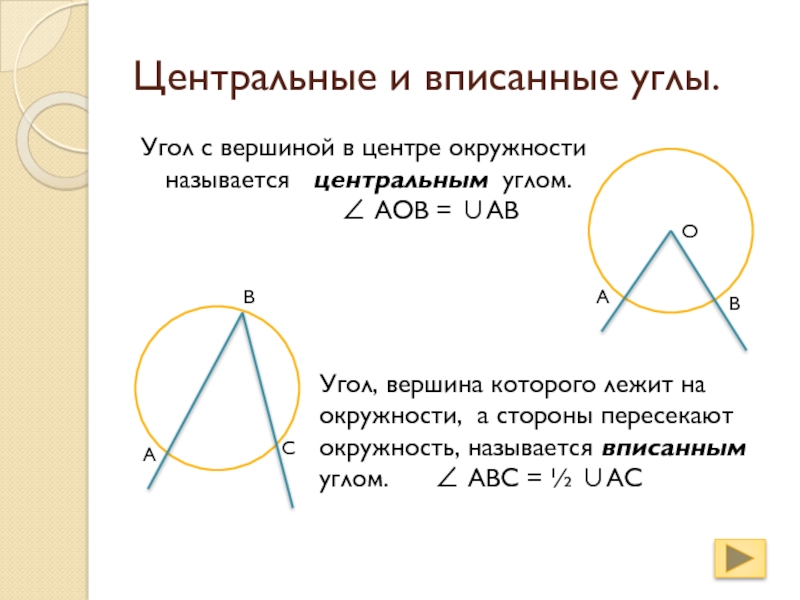
Угол с вершиной в центре окружности называется
центральным углом.
АОВ = АВУгол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. ABC = ½ AC
Слайд 18Вписанные углы.
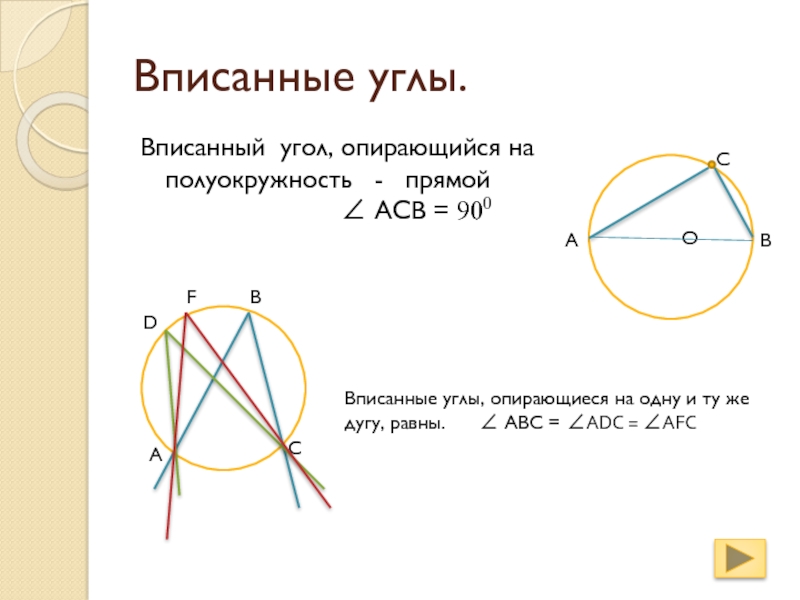
Вписанный угол, опирающийся на полуокружность - прямой
О
В
А
Вписанные углы, опирающиеся на одну и ту же дугу, равны. ABC = ADC = AFC
C
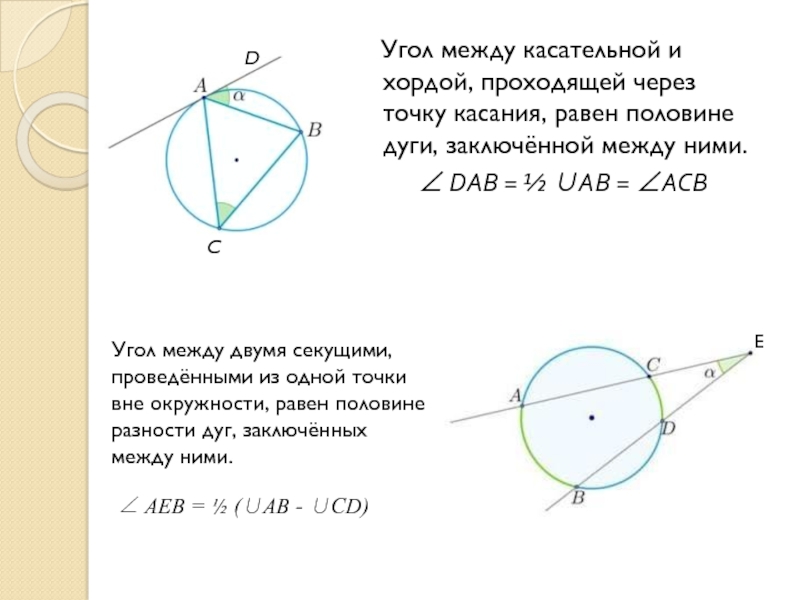
Слайд 19 Угол между касательной и хордой, проходящей через точку
касания, равен половине дуги, заключённой между ними.
DAB = ½ AB = ACBУгол между двумя секущими,
проведёнными из одной точки вне окружности, равен половине
разности дуг, заключённых
между ними.
AEB = ½ (AВ - CD)