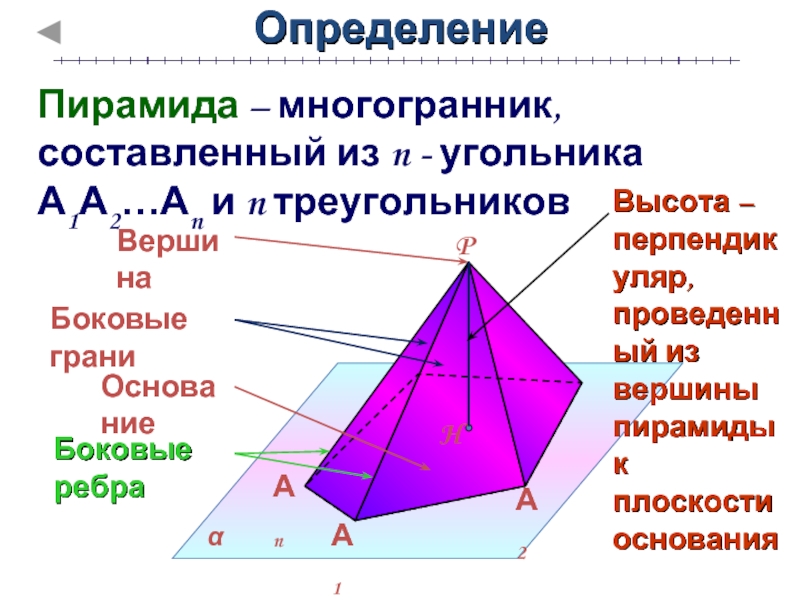
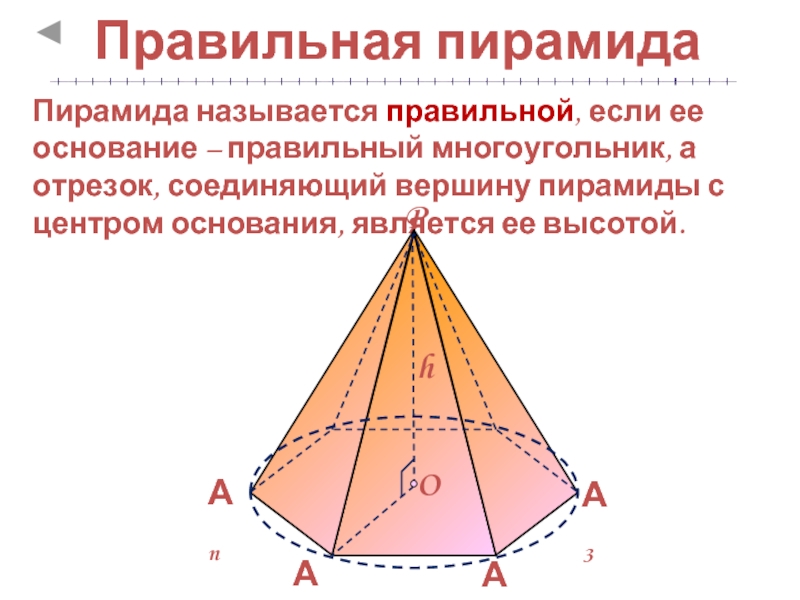
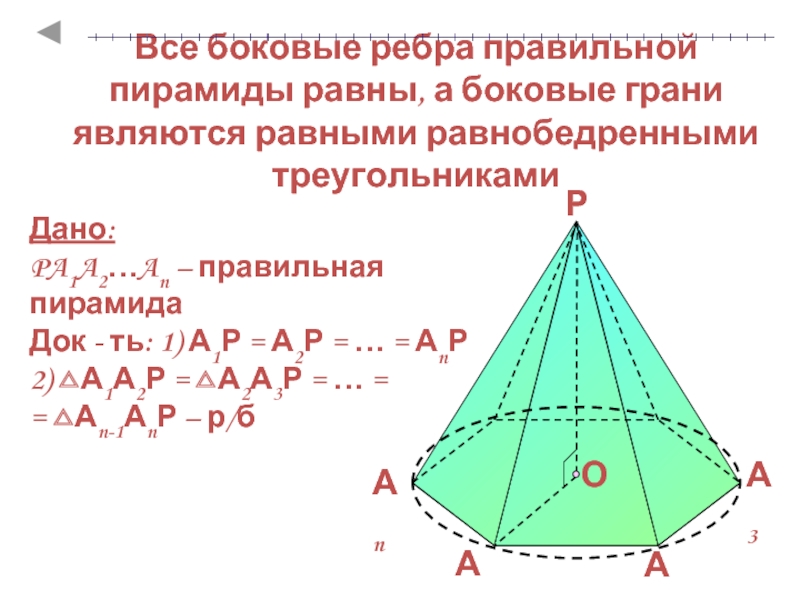
Пирамиды

пирамиды
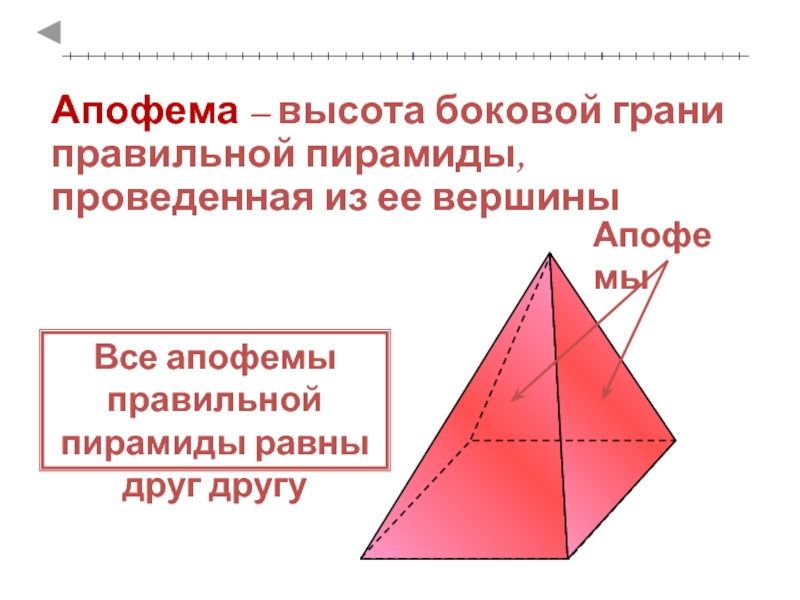
Апофема
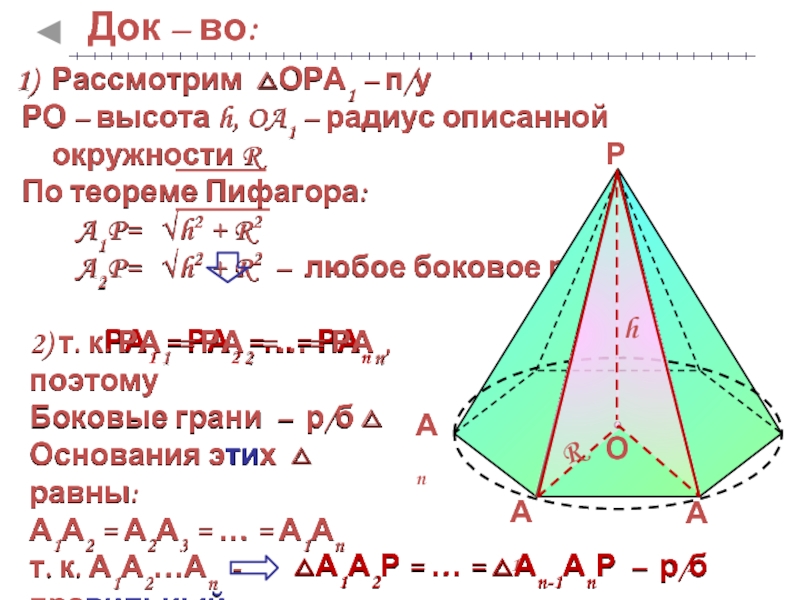
Теорема о площади боковой поверхности правильной пирамиды
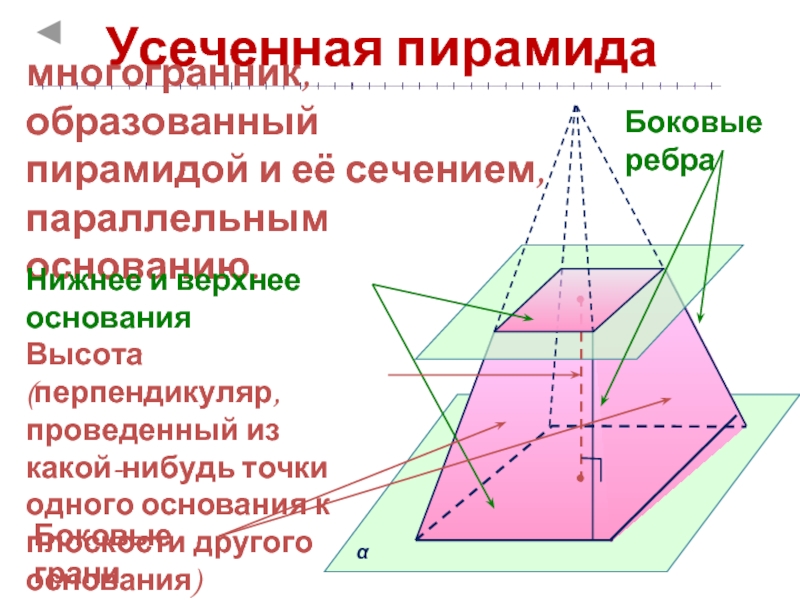
Усеченная

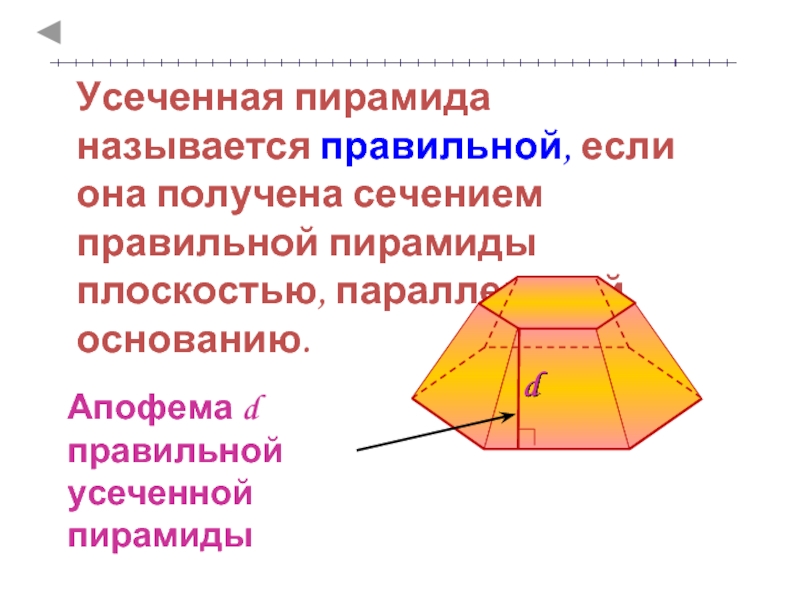
пирамида
Правильная усеченная пирамида
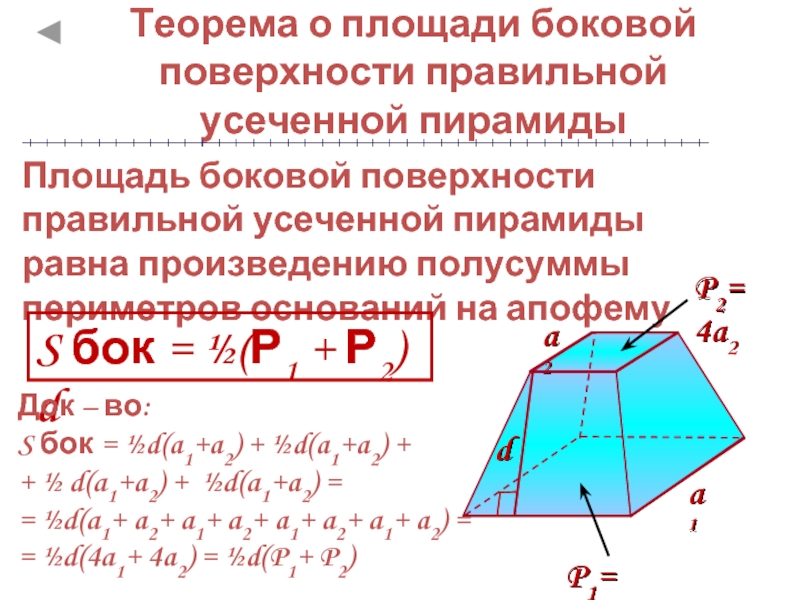
Теорема о площади боковой поверхности правильной усеченной пирамиды

и Вавилоне, однако активное развитие получило в Древней Греции. Первый,

кто установил, чему равен объем пирамиды, был Демокрит а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.

n треугольников
Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости

основания

Боковые ребра

а отрезок, соединяющий вершину пирамиды с центром основания, является ее

высотой.

равными равнобедренными треугольниками
Дано:
PA1A2…An – правильная пирамида
Док - ть: 1) А1Р

= А2Р = … = АnР
2) А1А2Р = А2А3Р = … =
= Аn-1АnР – р/б

поэтому
Боковые грани – р/б 
Основания этих  равны:

А1А2 = А2А3 = … = А1Аn
т. к. А1А2…Аn - правильный многоугольник

А1А2Р = … = Аn-1АnР – р/б

вершины
Все апофемы правильной пирамиды равны друг другу
Апофемы

пирамиды равна половине произведения периметра основания на апофему
Док – во:
Sбок

= (½ad + ½ad + ½ad) =
= ½d(a + a + a)= ½dP

Sбок = ½dP

и верхнее основания
Боковые грани
Боковые ребра
Высота (перпендикуляр, проведенный из какой-нибудь точки

одного основания к плоскости другого основания)

плоскостью, параллельной основанию.
Апофема d правильной усеченной пирамиды

правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему
S

бок = ½(Р1 + Р2) d

P1= 4a1

P2= 4a2

Док – во:
S бок = ½d(a1+a2) + ½d(a1+a2) +
+ ½ d(a1+a2) + ½d(a1+a2) =
= ½d(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) =
= ½d(4a1+ 4a2) = ½d(P1+ P2)