Слайд 1Построение сечений и определение площади в задачах повышенного уровня
Слайд 2Цели урока:
Образовательные: актуализировать знания о сечениях в прямоугольном параллелепипеде, пирамиде;
рассмотреть практическое применение формул для вычисления площадей плоских фигур
Воспитательная: развитие
навыков коммуникативного общения в процессе решения задач, ответственности за результаты работы
Развивающие: развитие пространственного мышления, логики, умение критически оценивать результаты своего решения
Слайд 3Методы обучения:
Словесный
Наглядный
Эвристический
Форма обучения:
Коллективная
Работа в группах
Индивидуальная
Слайд 4Ход урока
Организационный момент: 2 мин
Проверка д/з : 5 мин
Актуализация знаний
по стереометрии: фронтальная работа по слайдам
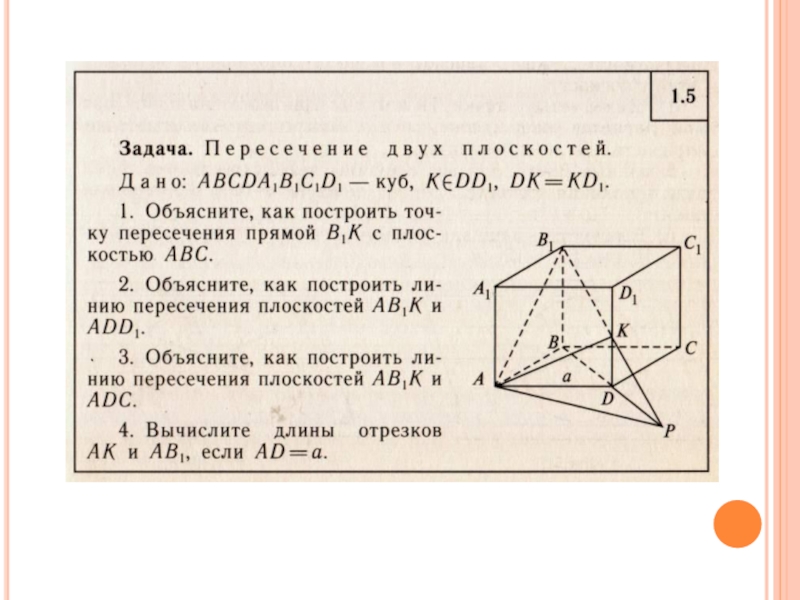
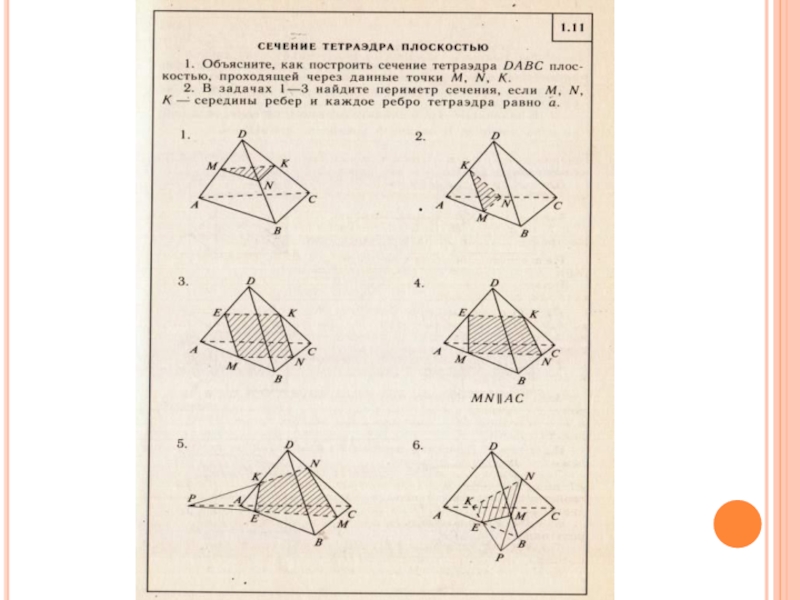
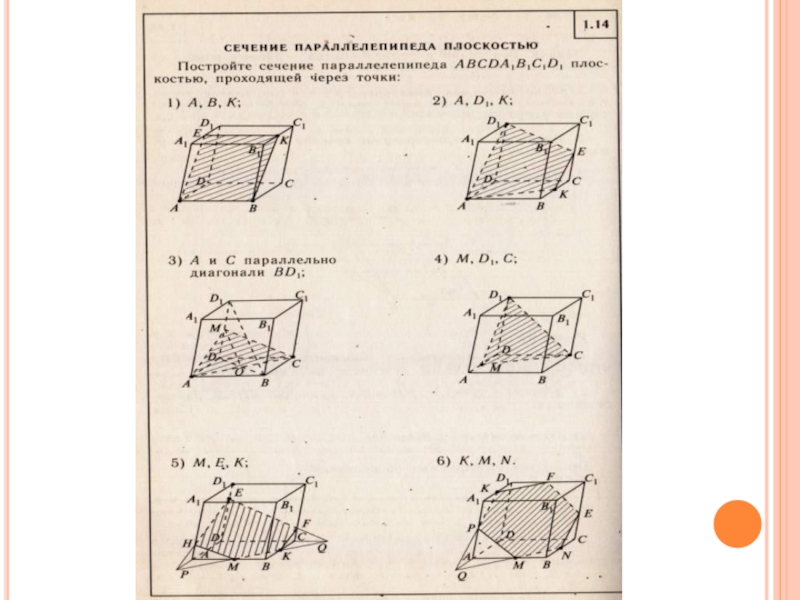
1.4, 1.5 стр.17, 1.11,1.12 стр.40, 1.14 стр.42
из пособия «Изучение геометрии в 10 и 11 классах»: 6 мин
Работа в группа: создание алгоритмов решения, построение сечений, вычисление площади сечений: 15мин
Слайд 5Защита решений полученных задач: 10 мин
Оценка деятельности каждой группы:
3 мин
Домашнее задание: 2 мин
Рефлексия: 2мин
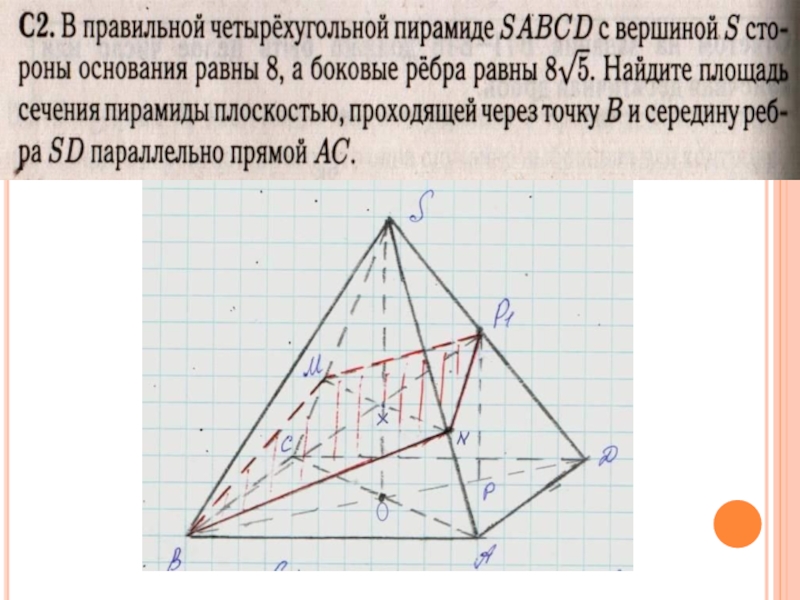
Слайд 10Решение С2:
1) В основании правильной пирамиды лежит квадрат ABCD.
Проведем
SO┴(ABC), BP∩SO = X. Через точку X проведем MN║AC, K
– середина SP1, следовательно, AMKN - искомое сечение , BP – ось симметрии, BP ┴MN и
S(BEKF)=1/2*MN*BK
2) Диагонали квадрата равны, т.е. BD=AC=8√2;
Из ∆SOD ( угол SOD= 90˚) по теореме Пифагора:
SO=√(SD²-OD²)=√(8√2)²-(4√2)²)=√(320-32)=12√2
Слайд 11 3) Проведем P1P┴BD, тогда P1P║SO, P1P=1/2*SO, так как K-
середина SD, следовательно, по теореме Фалеса P- середина OD. P1P=6√2,
OP = 1/2*OD=2√2, тогда
BP=BO+OP=4√2+2√2=6√2
BP=P1P =6√2 . Из ∆ BKP по теореме Пифагора
BP=√(2*BP²)=BP√2=12
4) BP1 ∩ SO и BP1 и SO – медианы, следовательно, SX/SO=2/3
∆SMN~ ∆SCA( угол S- общий, угол SMN=SCA-как соответственные при AC║MN и секущей SC)
AC/MN=SO/SX; MN=(AC*SX)/SO=2/3AC=16√2/3
Слайд 12
5)S(BMKN)=1/2MN*BP1 =1/2*12*16√2/3=32√2
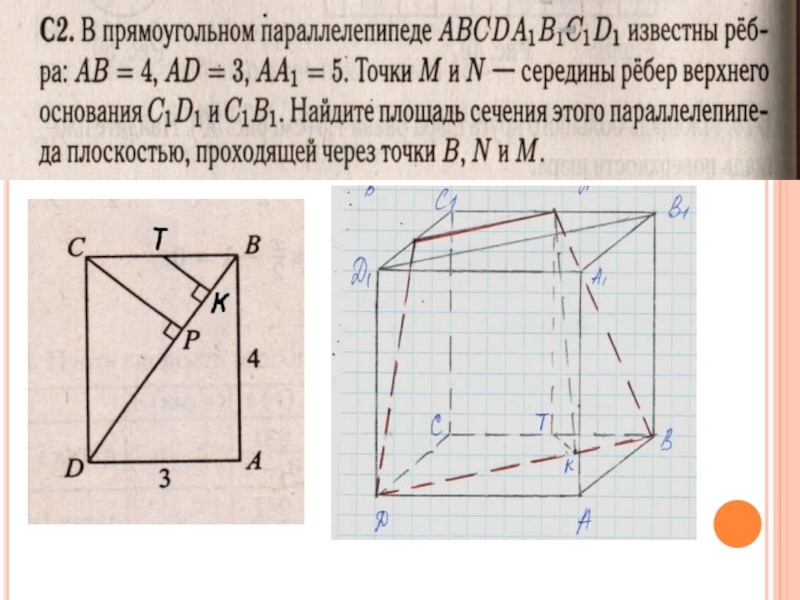
Слайд 14Решение С2
1)MN-средняя линия ∆B1C1D1 – по условию, тогда MN║B1D1 ,но
В1D1 ║BD , следовательно, MN║BD и BNMD-трапеция
2) Рассмотрим основание
параллелепипеда ABCD
Угол А=90˚, AD=3, AB=4, тогда BD=5, B1D1 =BD=5, MN=1/2B1D1 =2,5
Т-середина BC, следовательно, BT=1,5, BK=1/2BP по теореме Фалеса CP=CD*CB/DB=3*4/5=12/5
TK=1/2CP=1/2*12/5=1,2
Слайд 153) Найдем высоту MNBD:
Из ∆NTK(угол NTK=90˚)
по теореме Пифагора
NK=√(NT²+TK²)=√(25+36/25)=√(661/25)
NK=√661/5
4) S(BDMN)=1/2(MN+BD)*NK
S=1/2*(2,5+5)*√661/ 5=0,75*√661
Ответ: 0,75*√661
Слайд 16Литература
Атанасян Л.С., Бутузов В.Ф. и др. «Геометрия 10 класс»
Саакян С.М.
и Бутузов В.Ф. « Изучение геометрии в 10-11 классах»
Подготовка к
ЕГЭ-2015 Лысенко Ф.Ф., Кулабухова С.Ю.
Поурочные планы