Понятие конуса. Площадь поверхности конуса. Усеченный конус.

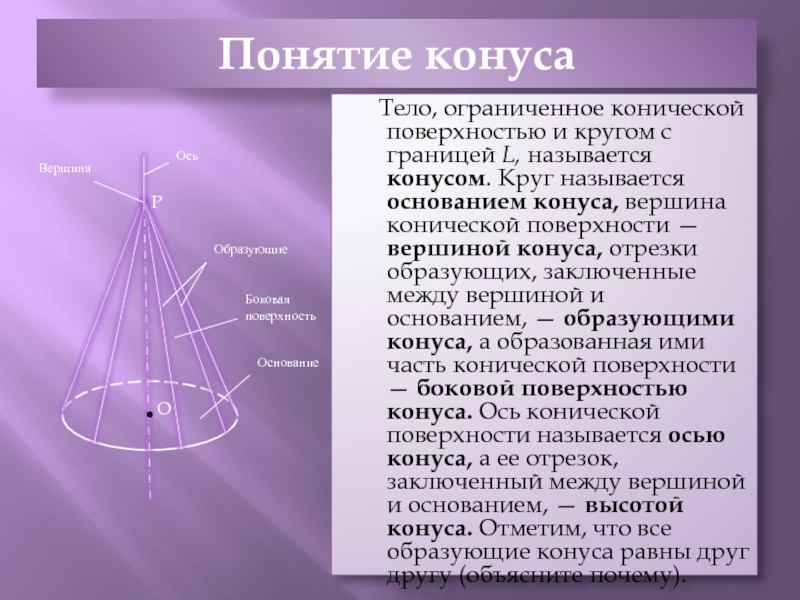
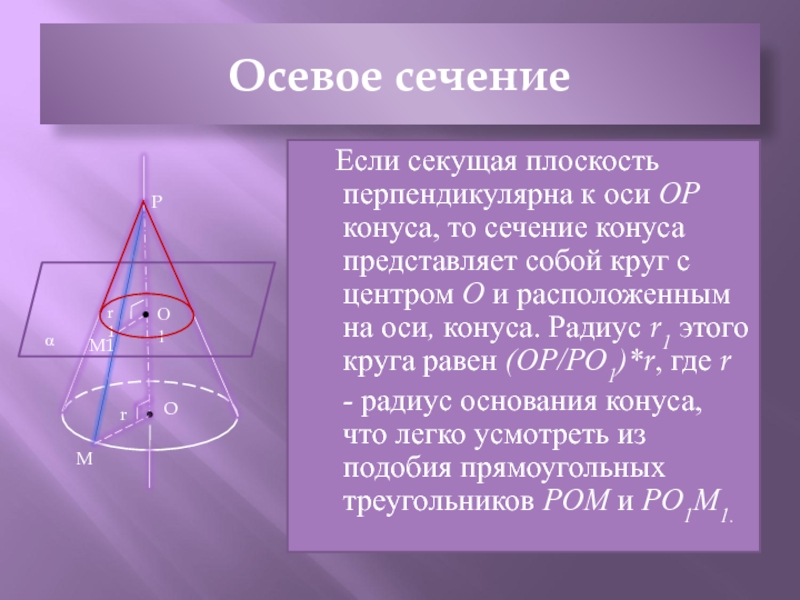
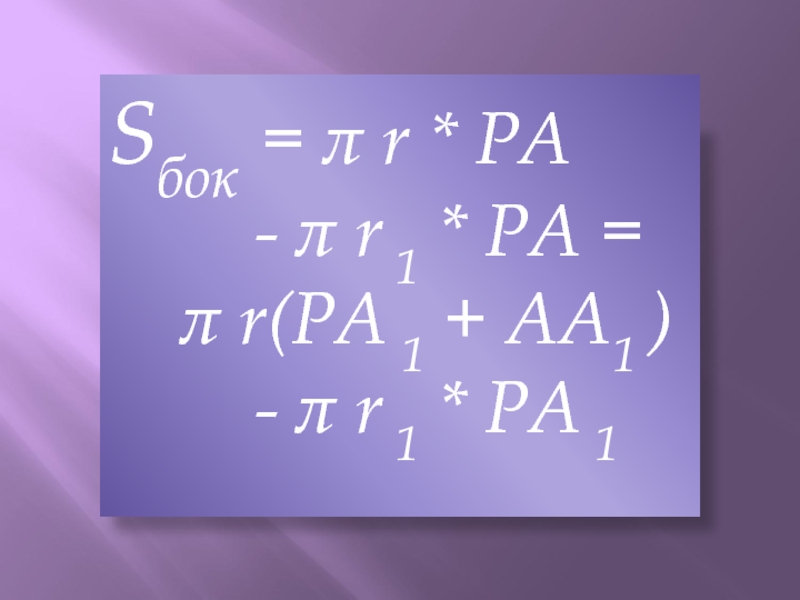прямую ОР, перпендикулярную к плоскости α этой окружности. Через точку

Р и каждую точку окружности проведем прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. Точка Р называется вершиной, а прямая OР – осью конической поверхности.

α

О

L

P

называется конусом. Круг называется основанием конуса, вер­шина конической поверхности —

вершиной конуса, отрезки образующих, заключенные между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности — боковой поверх­ностью конуса. Ось конической поверхности называ­ется осью конуса, а ее отрезок, заключенный между вершиной и основанием, — высотой конуса. Отметим, что все образующие конуса равны друг другу (объ­ясните почему).

O

P

Ось

Вершина

Образующие

Боковая поверхность

Основание

вокруг одного из его катетов. На рисунке изображен конус, полученный

вращением прямоугольного треугольника ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС.

В

А

С

через ось конуса, то сечение представляет собой равнобедренный треугольник, основание

которого — диаметр основания конуса, а боковые стороны — образующие конуса. Это сечение называется осевым.

сечение конуса представляет собой круг с центром О и расположенным

на оси, конуса. Радиус r1 этого круга равен (ОР/РО1)*r, где r
- радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1.

O

P

M

О1

r

r1

M1

α

можно развернуть на плоскость, разрезав ее по одной из образующих.

Разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

В

Р

А

Р

А

В

А|

развертки. Выразим площадь Sбoк боковой поверхности конуса через его образу­ющую

I и радиус основания r. Площадь кругового сектора — развертки боковой поверхности конуса равна
πl2α
360
Где α – градусная мера дуги АВАI , поэтому

длина дуги ABA' равна 2πr (длине окружности основания конуса), то

2πr = (πl/180)* α, откуда

α

=

360 r

l

πrl
(2)

половины длины окружности основания на образующую.
Площадью полной поверхности конуса называется

сумма площадей боковой поверхности и основания. Для вычисления площади SКОН полной поверхности конуса получается формула

его оси. Эта плоскость пересекается с конусом по кругу и

разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры,— высотой усеченного конуса.

O

P

О1

r1

Основание

Образующая

Основание

r

Боковая поверхность

поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называются

образующими усеченного конуса. Все образующие усеченного конуса равны друг другу.

ее боковой стороны, перпендикулярной к основаниям. На рисунке изображен усеченный

конус, полученный вращением прямоугольной трапеции ABCD вокруг стороны CD, перпендикулярной к основаниям AD и ВС. При этом боковая поверхность образуется вращением боковой стороны АВ, а основания усеченного конуса — вращением оснований СВ и DA трапеции.

С

В

А

D

полусуммы длин окружностей оснований на образующую, т. е.
Sбок = π

(r + r1 ) l

Где r и r1 – радиусы оснований, l – образующая усеченного конуса.

получен усеченный конус, АА1 — одна из образующих усеченного конуса,

r > r1 точки О и О 1 — центры оснований. Используя формулу (2), получаем

O

P

A

О1

r1

- π r 1 * PA =
π

r(PA 1 + AA1 )
- π r 1 * PA 1

- r1 ) PA 1

Выразим PA 1 через l, r

и r1. Прямоугольные треугольники РО1А1 и РОА подобны, так как имеют общий острый угол Р, поэтому

(3)

1
=
r 1
r
PA 1
=
l r 1
r - r 1

формуле