Понятие многогранника. Призма

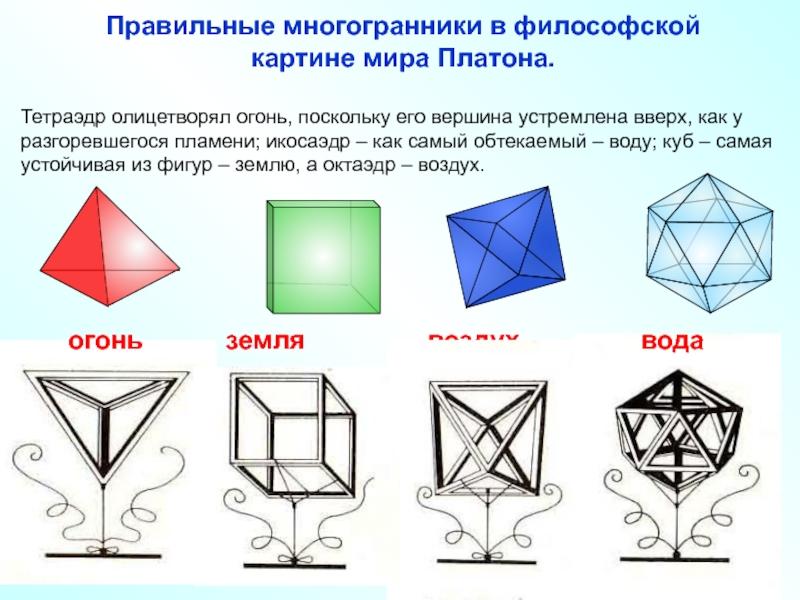
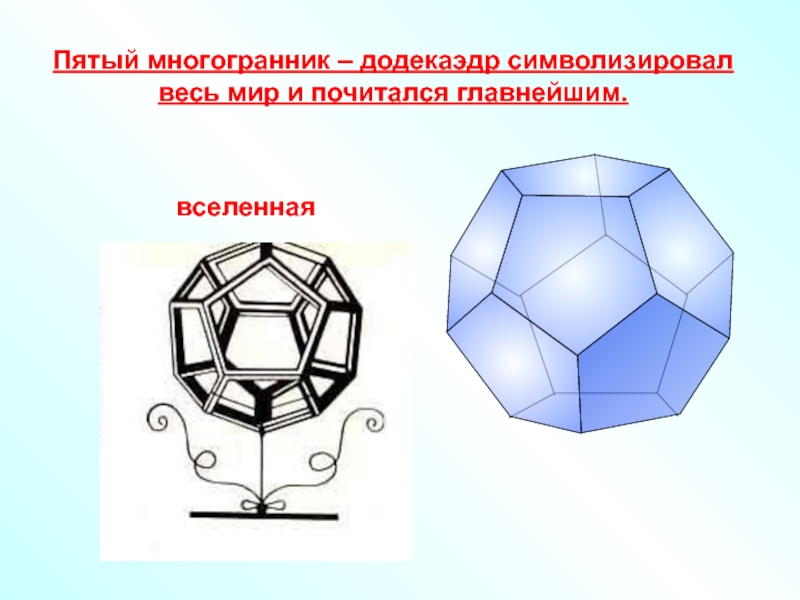
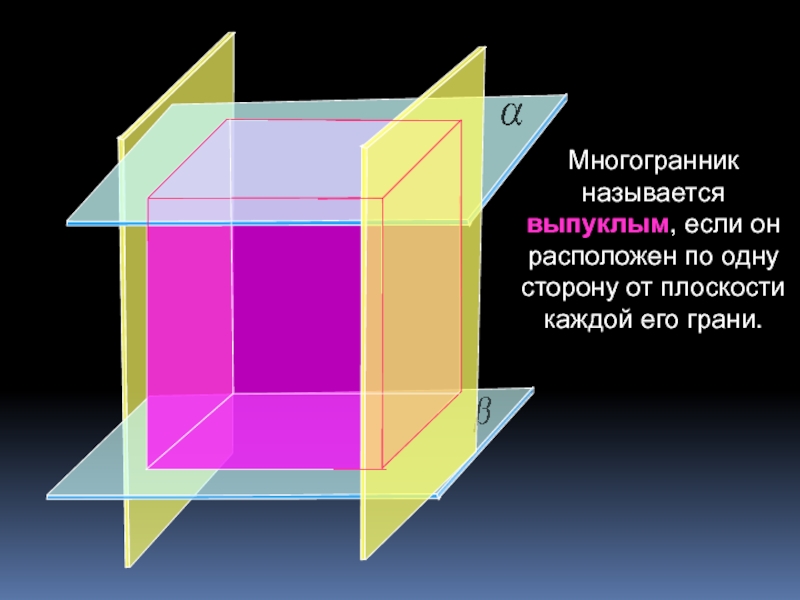
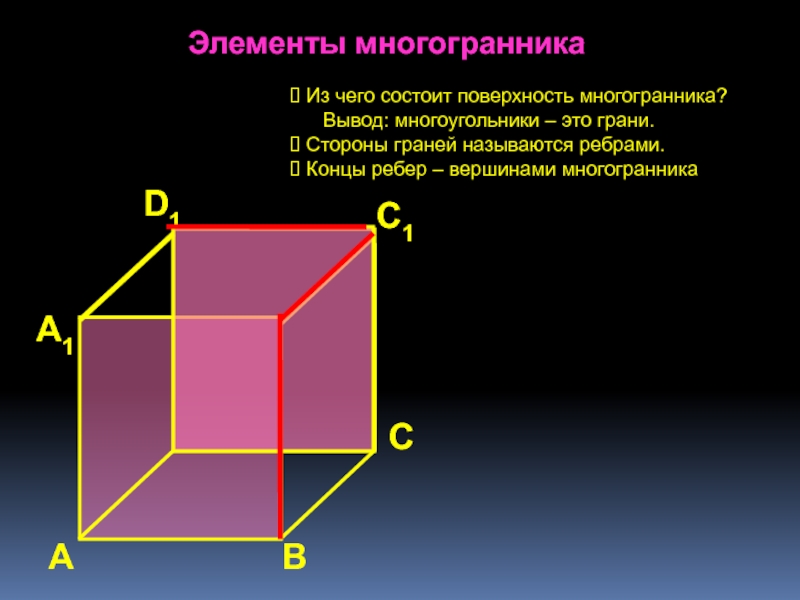
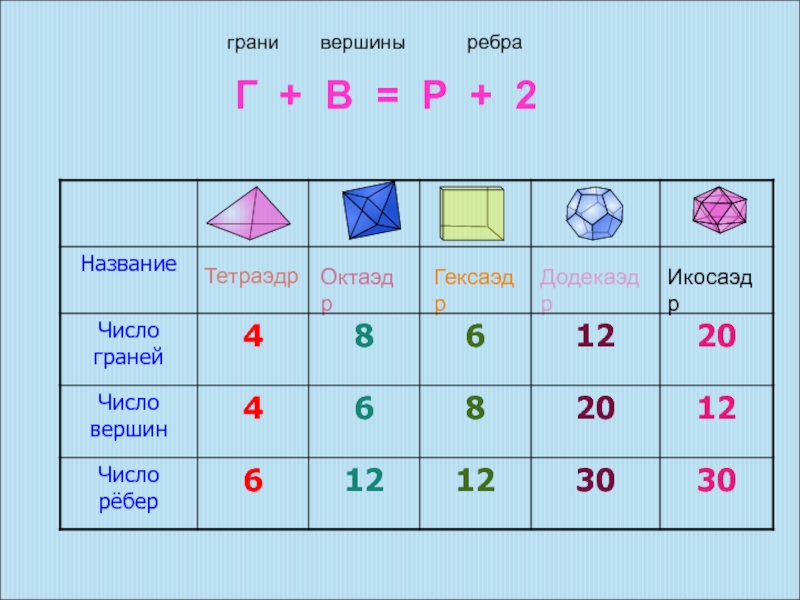
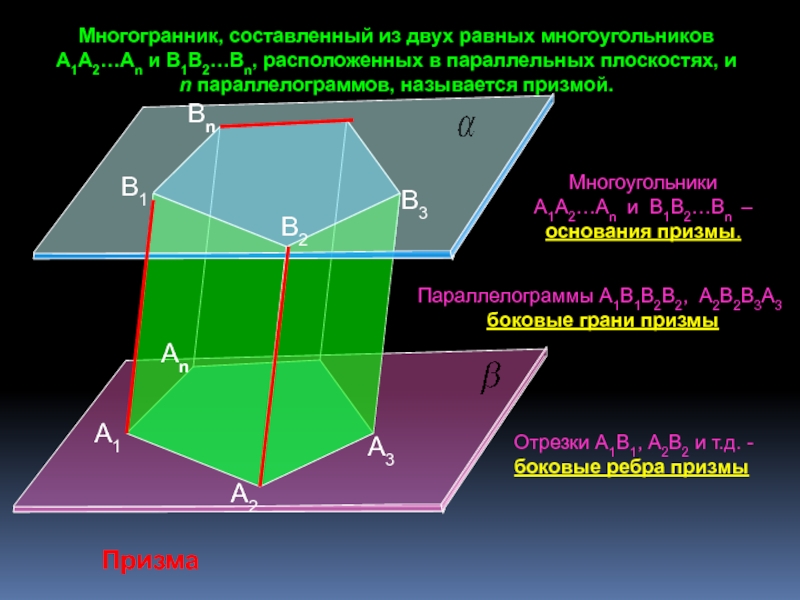
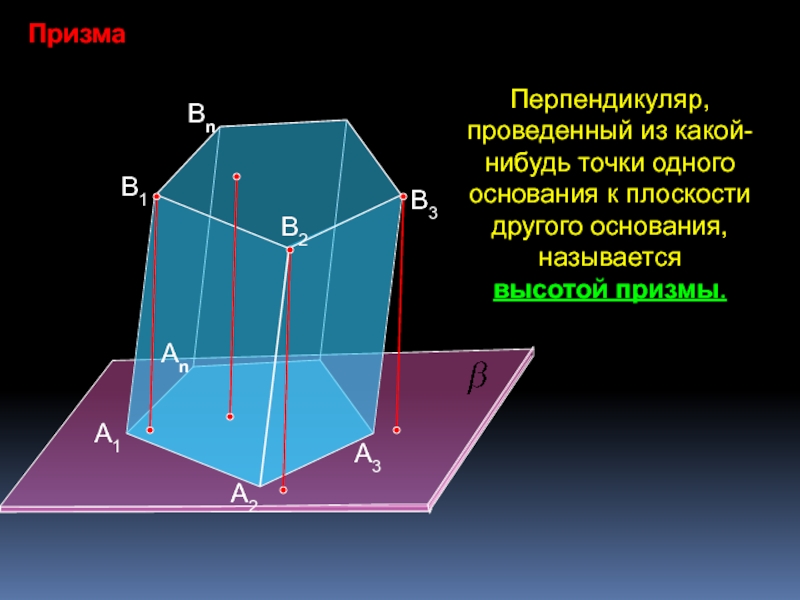
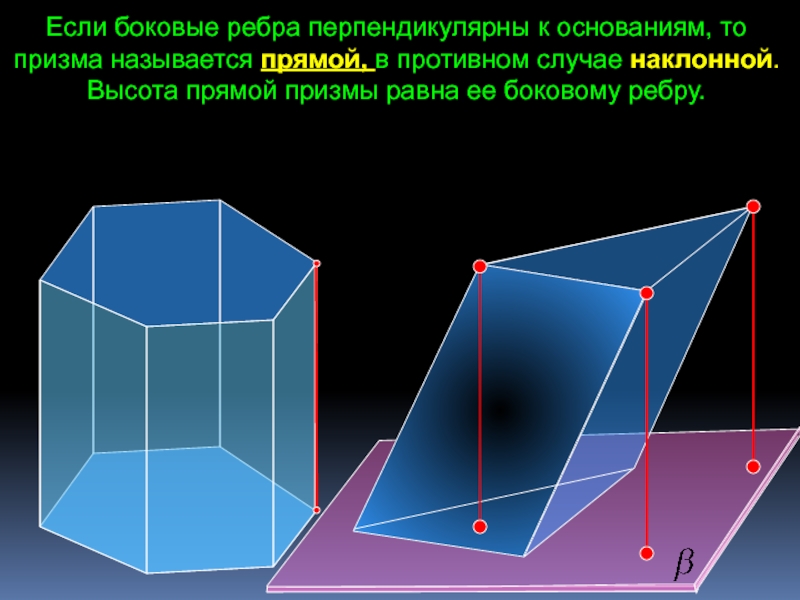
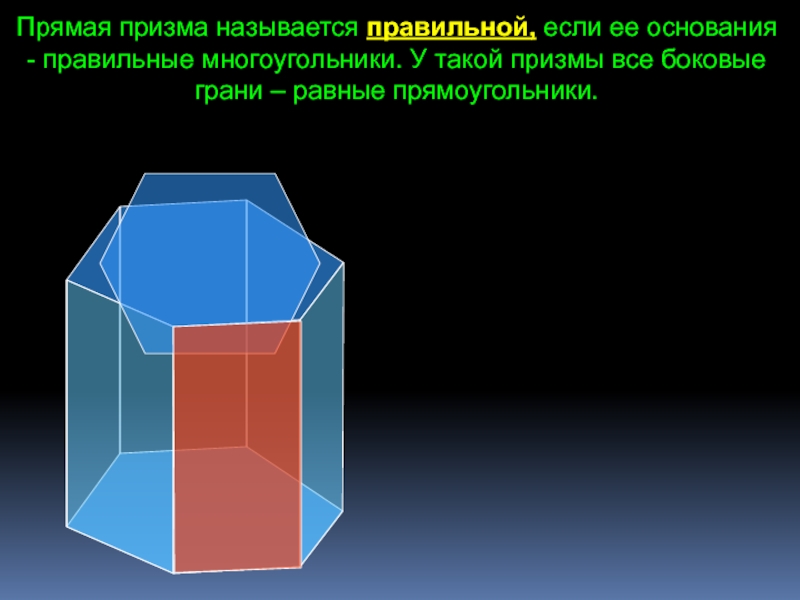
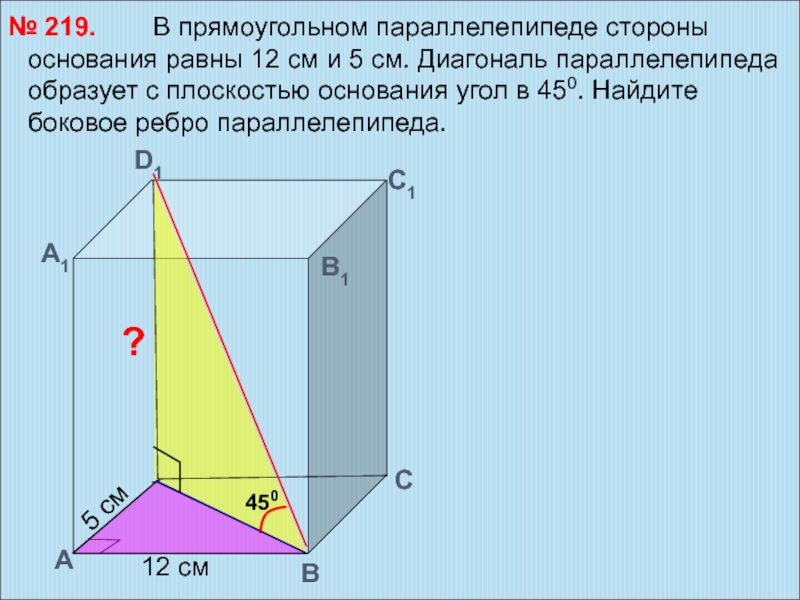
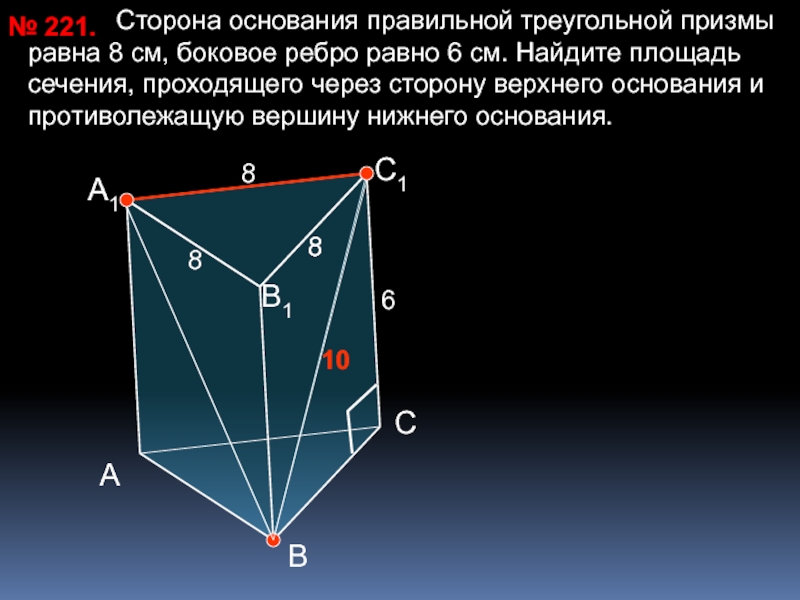
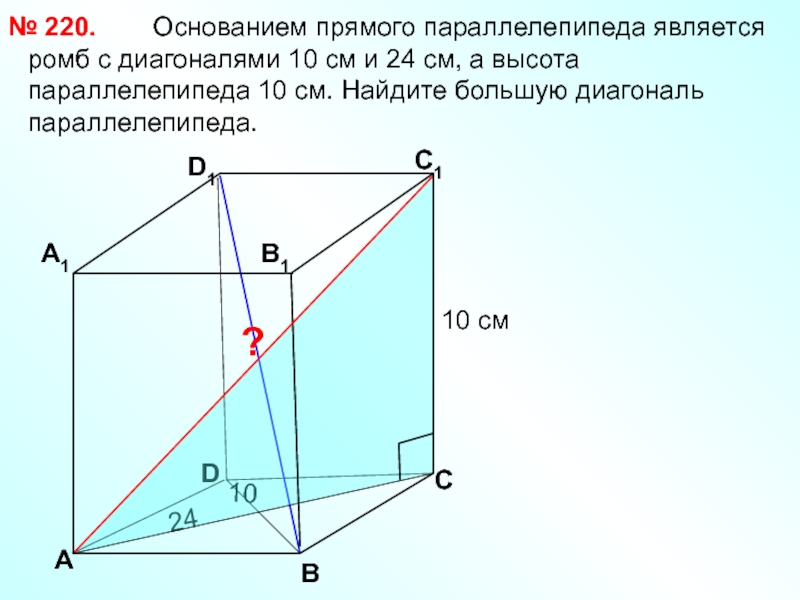
познавательная: формирование умений применять основные понятия многогранника, призмы и их

элементов при решении задач на конструктивном уровне

Задачи:

Развивающая: развитие визуального, наглядно-образного типов мышления.

Воспитательная: способствовать развитию устойчивого интереса к математике через применение информационно – коммуникационных технологий.

отряд сумел пробраться в самые глубины различных наук»

Л.Кэрролл

на корабль без руля и компаса и потому никогда не

знающему,
куда он плывет".         

Леонардо да Винчи

Чему равна сумма углов треугольника?
        

1

2

3

1800

Свойства углов при основании равнобедренного треугольника.         

1

2

1 = 2

Что называется углом между прямой и плоскостью?         

М

А

β0

Что называется линейным углом двугранного угла?         

А

В

О

Вавилон)

Соразмерность и красота правильных
многогранников поражали древних греков
(Пифагорейская школа)

правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные многогранники

называют также телами Платона.

поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр

– как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.

геометрическое тело называют многогранником.


Многогранники бывают

Выпуклые
Невыпуклые
Прямые
Наклонные

плоскости каждой его грани.

многоугольники – это грани.
Стороны граней называются ребрами.
Концы ребер

– вершинами многогранника

но чтобы образовался многогранный угол сумма их градусных мер должна

быть меньше 360°, т.е.
nα< 360°

Угол правильного треугольника равен 60°, значит в
одной вершине может сходиться
3, 4 или 5 правильных треугольников

Тетраэдр

Октаэдр

Икосаэдр

Существуют многогранники, гранями которых являются правильные треугольники

Угол квадрата равен 90°, значит в одной вершине может сходиться только 3 квадрата

Существуют многогранники, гранями которых являются правильные четырёхугольники

Гексаэдр

Угол правильного пятиугольника равен 108°, значит в одной вершине может сходиться только 3 правильных
пятиугольника

Существуют многогранники, гранями которых являются правильные пятиугольники

Додекаэдр

вершин равна числу рёбер, увеличенному на 2.
60°+ 60° + 60°

< 360°

4 грани, 4 вершины и 6 ребер.

Сумма плоских углов при каждой вершине равна 1800

в параллельных плоскостях, и n параллелограммов, называется призмой.
Многоугольники
А1А2…Аn и

В1В2…Вn – основания призмы.

Параллелограммы А1В1В2В2, А2В2В3А3
боковые грани призмы

Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы

основания, называется
высотой призмы.

в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

У такой призмы все боковые грани – равные прямоугольники.

на лыжах … : научиться этому можно лишь подражая избранным

образцам и постоянно тренируясь..
Д. Пойа

прямоугольном параллелепипеде стороны основания равны 12 см и 5 см.

Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.

№ 219.

В

С

А1

D1

С1

В1

?

А

12 см

5 см

призмы равна 8 см, боковое ребро равно 6 см. Найдите

площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.

№ 221.

А

В

С

С1

В1

А1

8

6

8

8

8

10

прямого параллелепипеда является ромб с диагоналями 10 см и 24

см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.

№ 220.

В

С

А1

D1

С1

В1

?

D

А

24

10

10 см

многогранник?
Какой многогранник называется выпуклым?
Дан куб – выпуклый многогранник.

Как, имея пилу, получить из деревянного куба модель невыпуклого многогранника?
Какими фигурами являются боковые грани призмы?
Какими фигурами являются все грани параллелепипеда?
Сколько измерений у прямоугольного параллелепипеда?
Назовите элементы многогранника.
О каких видах многогранников вы услышали сегодня на уроке?

красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному

совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел.