Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольные треугольники при решении задач С4 11 класс
Содержание
- 1. Прямоугольные треугольники при решении задач С4 11 класс
- 2. α + β = 90ºβ = 90
- 3. II. CD = (BC · AC) /
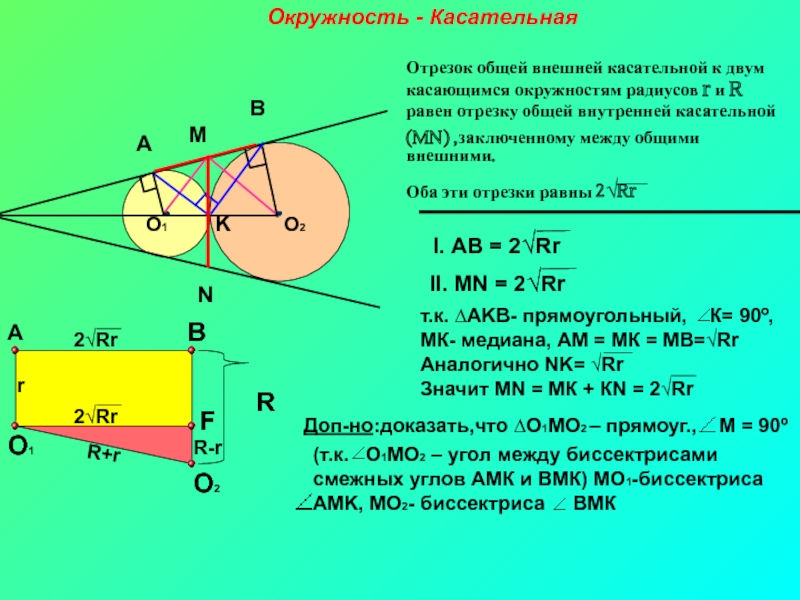
- 4. Окружность - Касательная
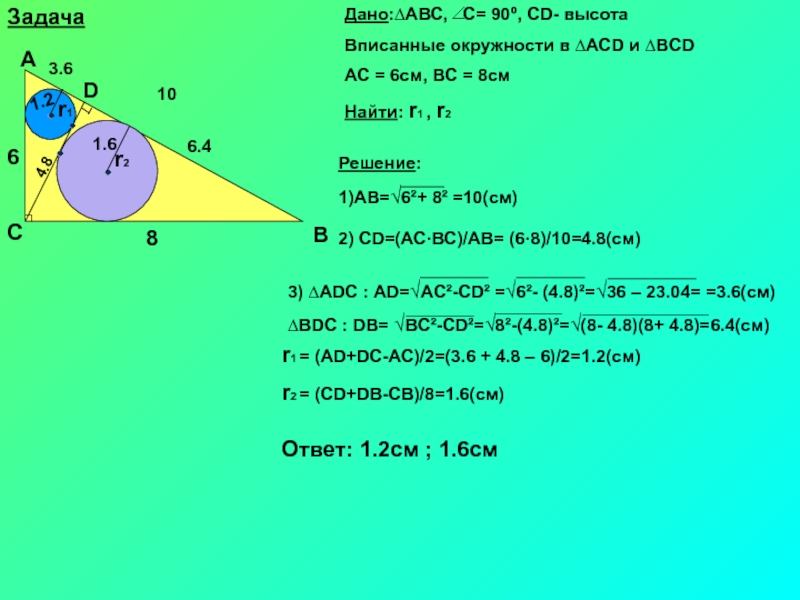
- 5. Задача
- 6. Окружности: вписанные, описанныеI.R=½c , r = ½(a+b-c)=
- 7. Вневписанная окружностьI. Определение. Окружность называется вневписанной в
- 8. ЗадачаОтвет: 1.2см ; 1.6см
- 9. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
α + β = 90º
β = 90 - α
Дано: ∆АВС,
АВ=ВС.
AD- биссектриса, DM┴AD
DM ∩ АС = MДоказать: CD = ½AM
Доказательство:
2) ∆APD- равнобедренный, AP=PD
5) CD = ½AM
3) ∆PDC- равнобедренный, PD=CD
Задача
Слайд 3II. CD = (BC · AC) / AB
AC = (n² + m²) / n
BC = (n² + m²) / m
Высота из вершины прямого угла
III. В подобных треугольниках АВС,АСD,ВСD имеет место равенство:
d²a+d²b=d²c ; (da, db, dc,-сходственные линейные элементы этих треугольников
P²∆ABC= P²∆ACD+ P²∆BCD
r²a+ r²b= r²c ; R²a + R²b= R²c
ra,rb,rc-радиусы вписанных окружностей в ∆ACD, ∆BCD, ∆ABC
h²a+h²b=h²c (ha,hb,hc, -высоты,опущенные из вершин прямых углов
Слайд 6Окружности: вписанные, описанные
I.R=½c , r = ½(a+b-c)= p-c
(p-полупериметр
p=½ (a+b+c))
r = S/p ; R=abc/4S
II. BN= d = p-b
; BN равен разности полупериметра p и противоположной стороны b
Слайд 7Вневписанная окружность
I. Определение. Окружность называется вневписанной в треугольник, если она
касается одной из сторон треугольника и продолжений двух других сторон.
II.
Центр вневписанной окружности- точка пересечения биссектрис внутреннего и внешних углов треугольника.III. BN=BM=p (полупериметр)
IV. Радиус вневписанной окружности
rb=p·tg(β/2)
ra =p·tg(α/2)
rc =p·tg(γ/2)
rb=S / (p-b)
ra=S / (p-a)
rc=S / (p-c)
ra + rb + rc = r + 4R
(сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности)