Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии в 9 классе по теме: "Повторение. Окружность. Круг"
Содержание
- 1. Презентация к уроку геометрии в 9 классе по теме: "Повторение. Окружность. Круг"
- 2. повторить …………..совершенствовать навыки …………..систематизировать и обобщить ……………ЦЕЛИ:
- 3. повторить теоретический материал по теме «Окружность. Круг.»;совершенствовать
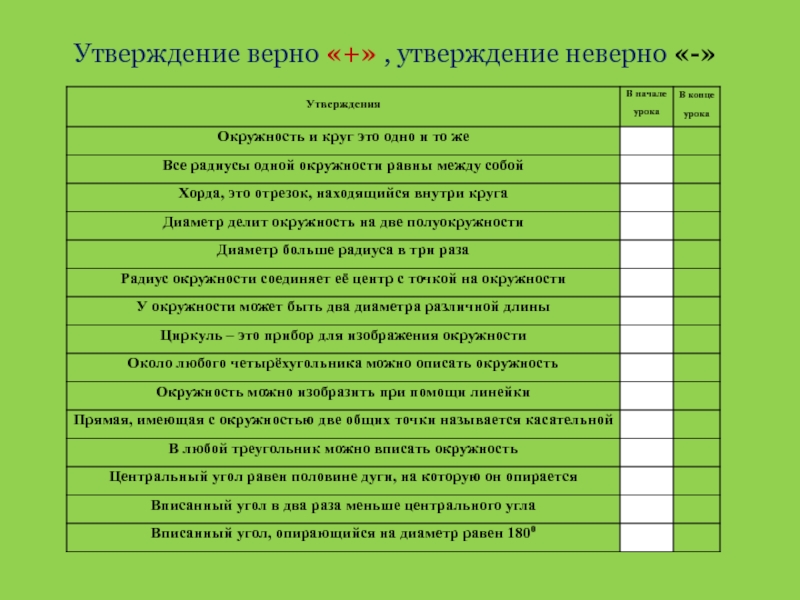
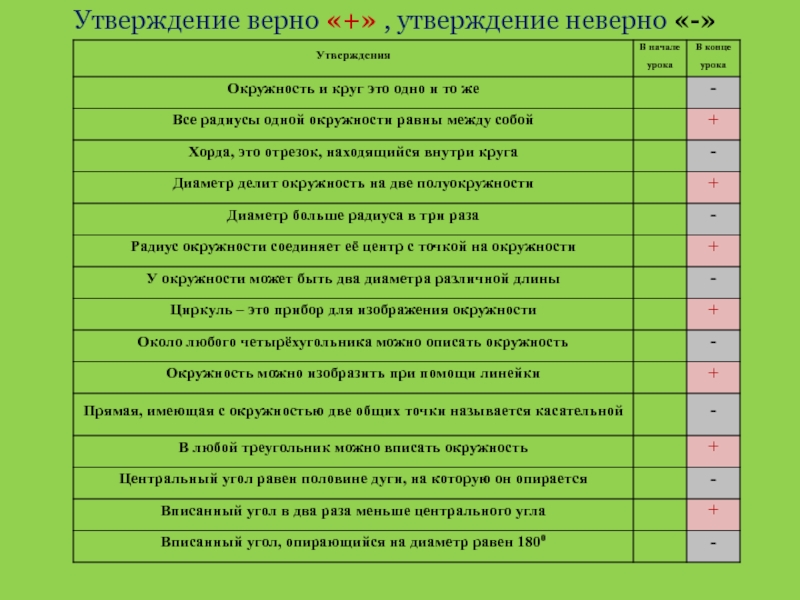
- 4. Утверждение верно «+» , утверждение неверно «-»
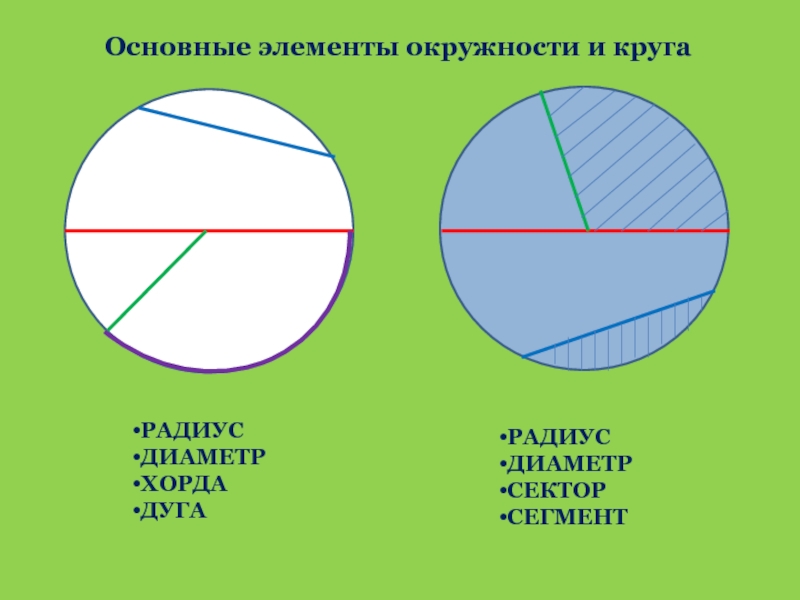
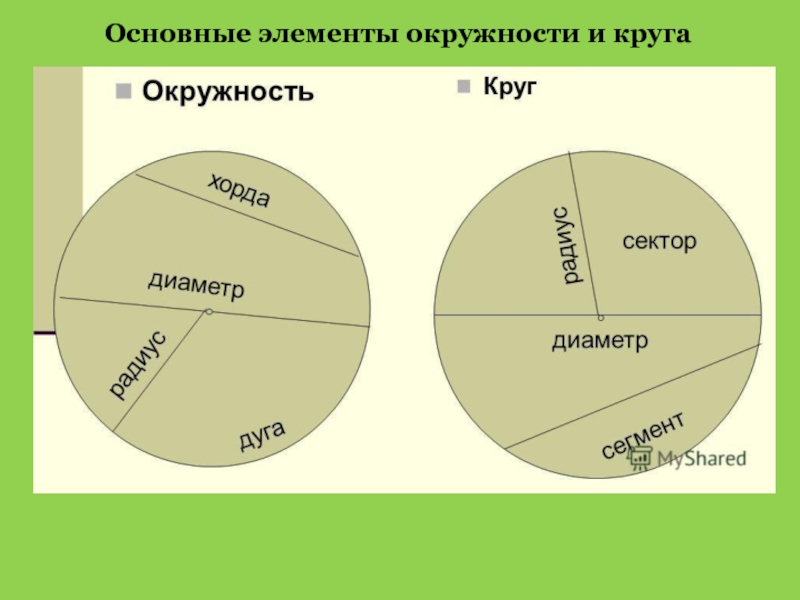
- 5. Основные элементы окружности и кругаРАДИУСДИАМЕТРХОРДАДУГАРАДИУСДИАМЕТРСЕКТОРСЕГМЕНТ
- 6. Основные элементы окружности и круга
- 7. Слайд 7
- 8. Окружность – геометрическая фигура, состоящая из всех
- 9. Колесо имеет 12 спиц. Углы между соседними
- 10. ЗАДАЧИ ПРО ЧАСЫ(задание № 15, ОГЭ модуль
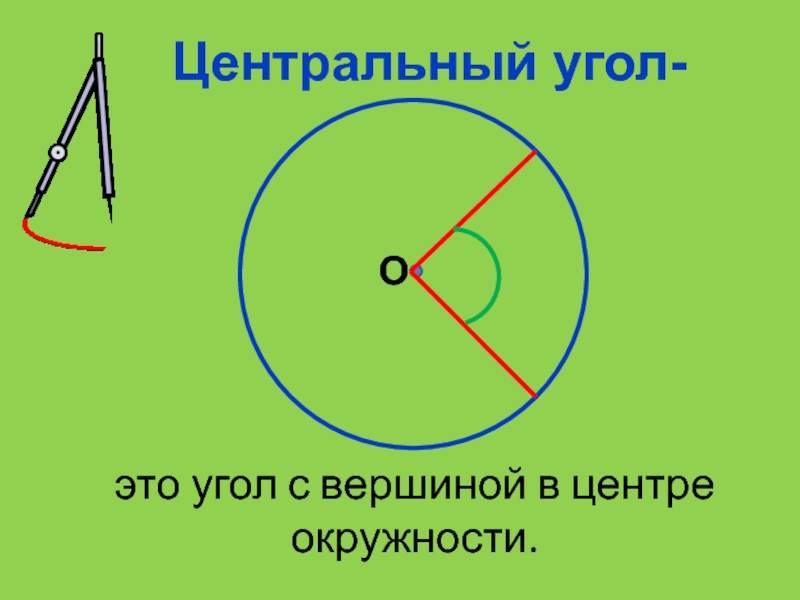
- 11. Центральный угол-это угол с вершиной в центре окружности.
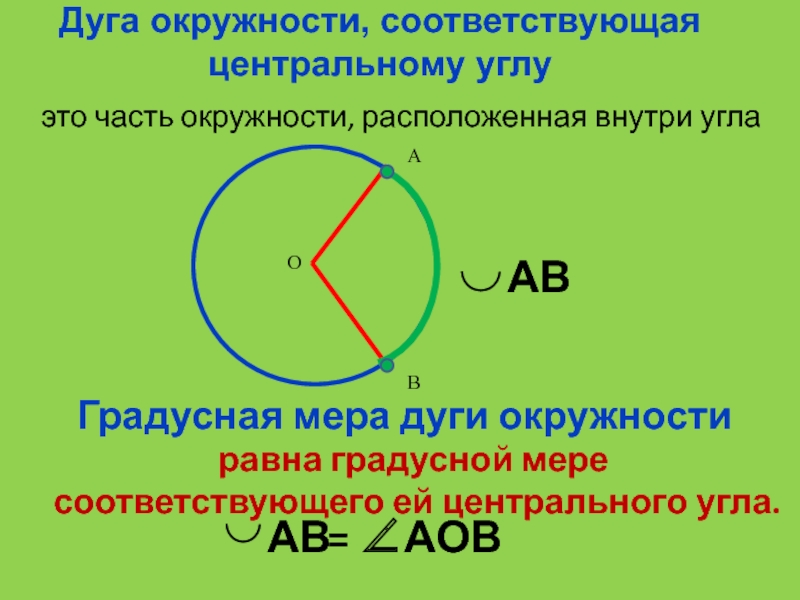
- 12. Дуга окружности, соответствующая центральному углуэто часть окружности,
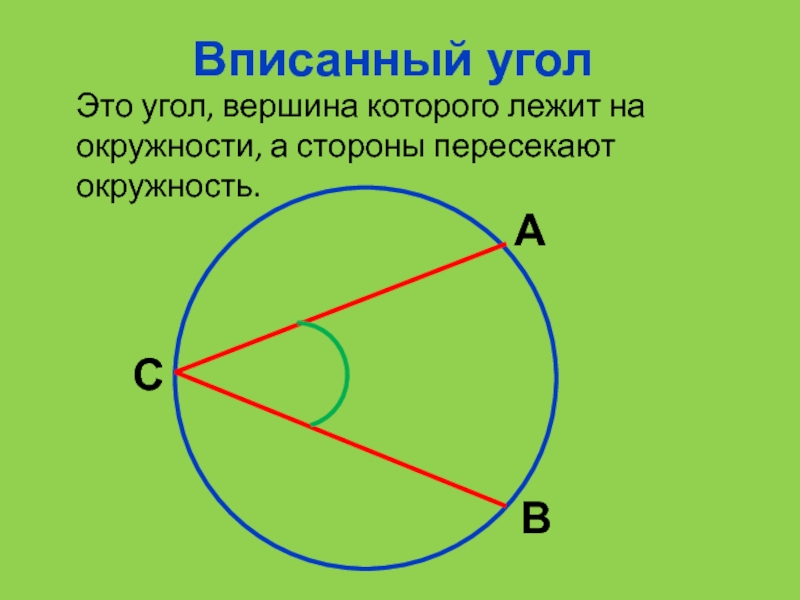
- 13. Вписанный уголЭто угол, вершина которого лежит на окружности, а стороны пересекают окружность.САВ
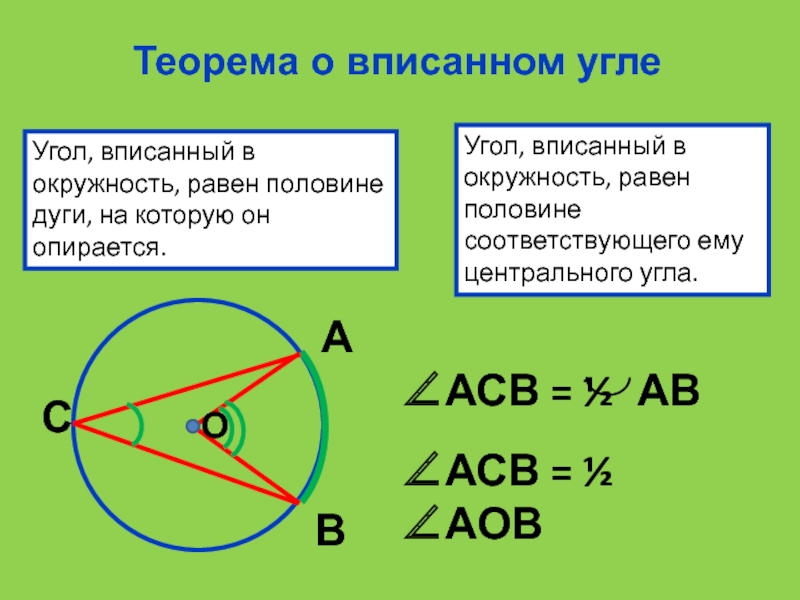
- 14. Теорема о вписанном углеУгол, вписанный в окружность,
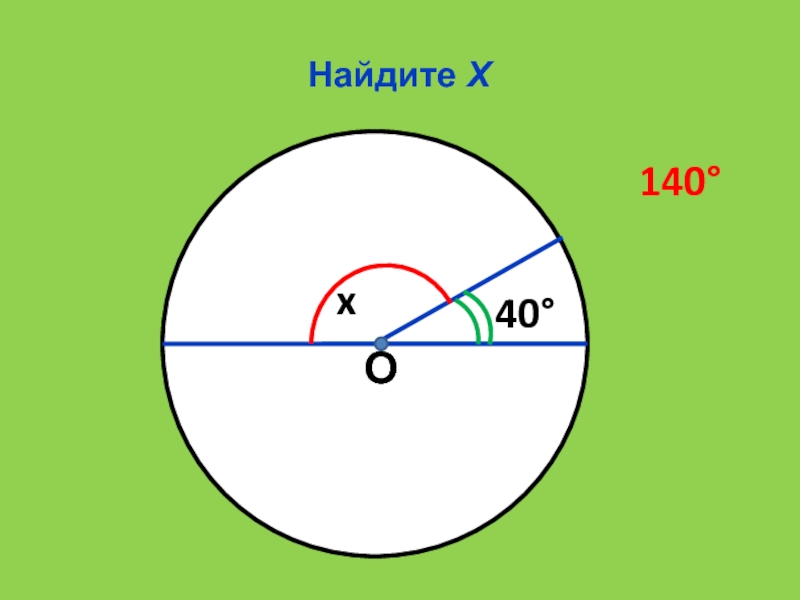
- 15. Найдите ХО x40140
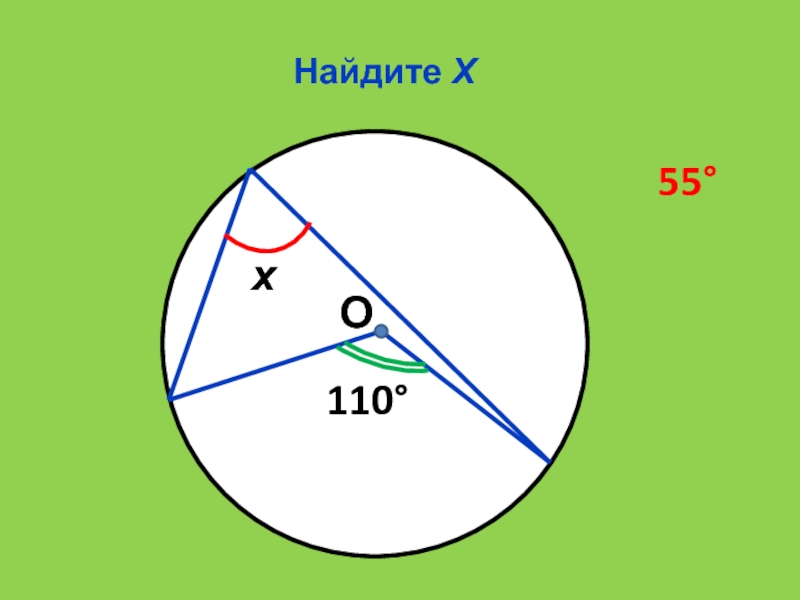
- 16. Найдите ХО110х55
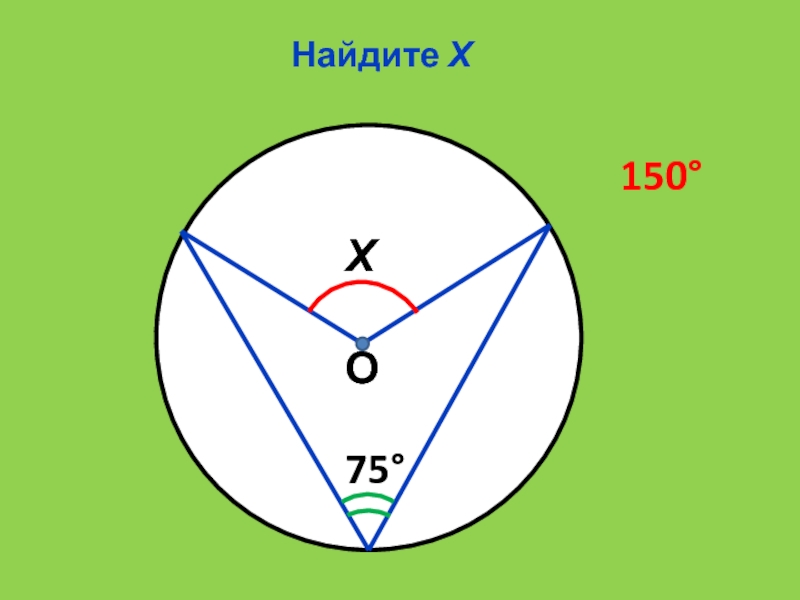
- 17. Найдите ХХ75150О
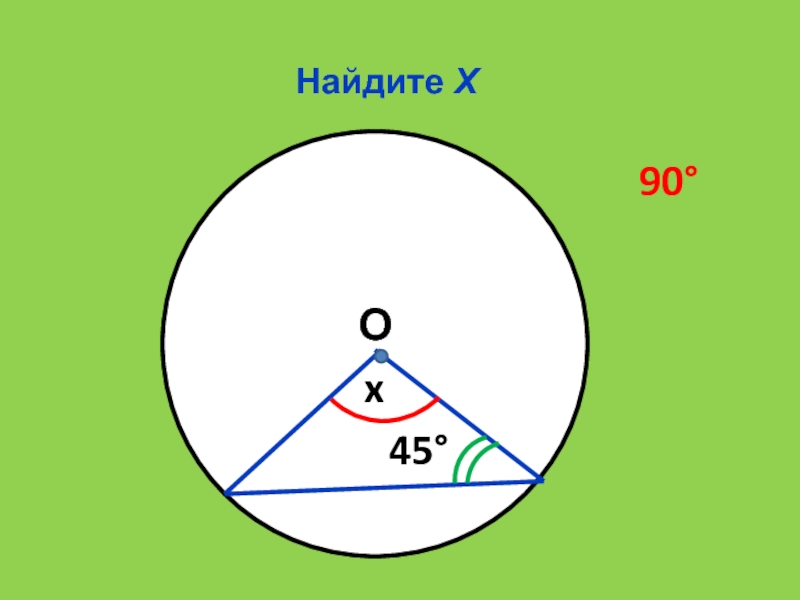
- 18. Найдите Хx4590О
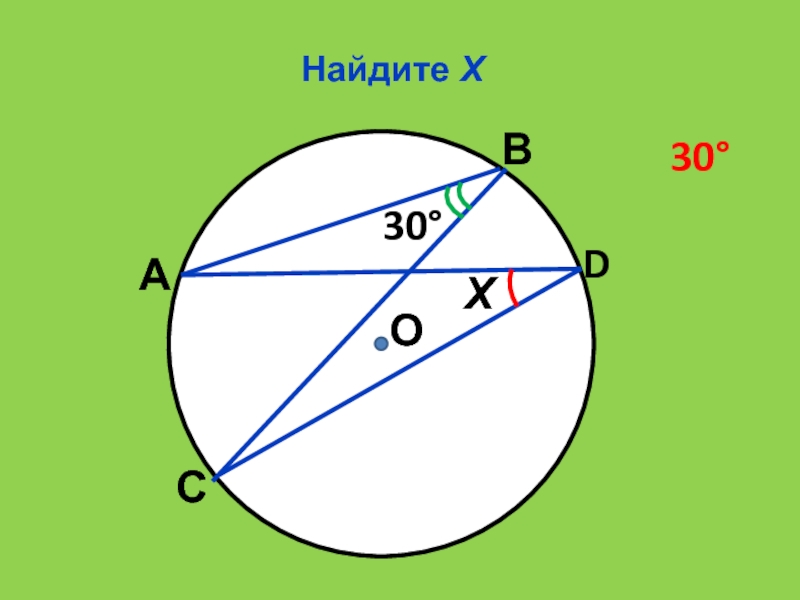
- 19. Найдите ХО30Х30АВСD
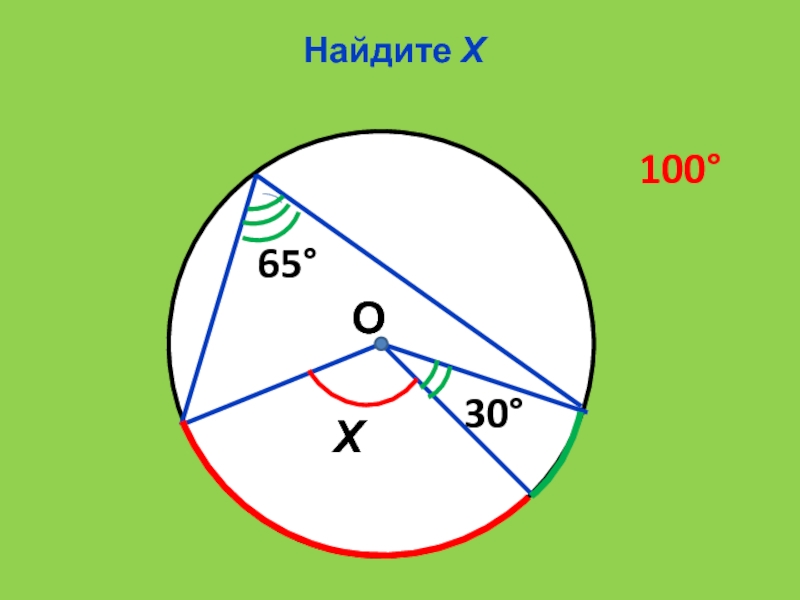
- 20. Найдите Х3065Х100О
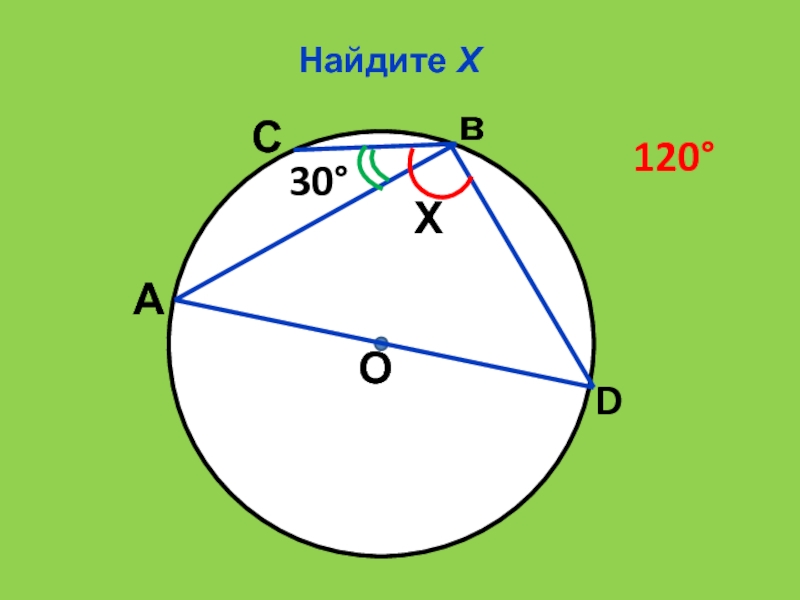
- 21. Найдите ХО30ХАСвD120
- 22. Из истории циркуля
- 23. Сейчас нельзя сказать, кто именно изобрел этот
- 24. КАК ПОСТРОИТЬ ОКРУЖНОСТЬБЕЗ ЦИРКУЛЯ
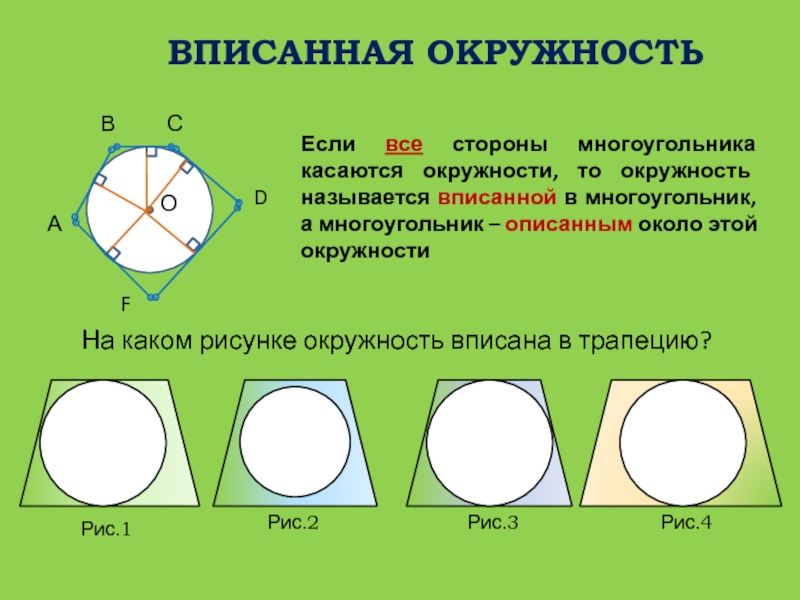
- 25. ВПИСАННАЯ ОКРУЖНОСТЬАВСDFОЕсли все стороны многоугольника касаются окружности,
- 26. ЗАМЕЧАНИЯ В треугольник можно вписать только
- 27. Свойство описанного четырехугольника В любом описанном четырехугольнике
- 28. ОПИСАННАЯ ОКРУЖНОСТЬАВСDFОЕсли все вершины многоугольника лежат на
- 29. ЗАМЕЧАНИЯ Около треугольника можно описать только одну
- 30. Свойство вписанного четырехугольника В любом вписанном четырехугольнике
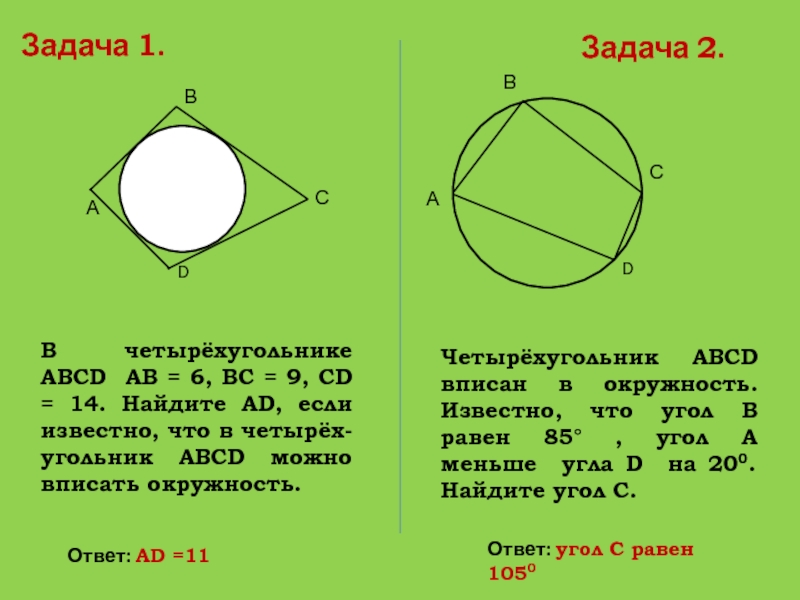
- 31. Задача 1.АВСDАВСDВ четырёхугольнике АВСD АВ = 6,
- 32. Задача №7 .Радиус OB окружности с центром
- 33. ЗАДАЧИ на нахождение площади1. Найдите площадь S
- 34. Выберите номера верных утверждений.1). Величина дуги окружности равна
- 35. Домашнее задание:1) Три задачи на выбор по
- 36. Утверждение верно «+» , утверждение неверно «-»
- 37. Задача № 11.В окружности с центром в
- 38. Слайд 38
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3повторить теоретический материал по теме «Окружность. Круг.»;
совершенствовать навыки решения задач
на примерах заданий из открытого банка ОГЭ по математике;
систематизировать и
обобщить знания по теме «Окружность. Круг.» для подготовки к экзаменам.ЦЕЛИ:
Слайд 8Окружность – геометрическая фигура, состоящая из всех точек плоскости, расположенных
на заданном расстоянии от данной точки.
Круг- часть плоскости, ограниченная окружностью;
Касательная
к окружности перпендикулярна к радиусу этой окружности, проведённому в точку касания;Отрезки касательных, проведённых к окружности из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности;
Центральный угол равен дуге окружности, на которую он опирается;
Вписанный угол окружности равен половине центрального угла
и измеряется половиной дуги, на которую он опирается;
7. Вписанный угол, опирающийся на диаметр окружности, равен 90◦;
8. Вписанные углы, опирающиеся на одну и ту же дугу равны;
9. В любом описанном четырехугольнике суммы противоположных сторон равны;
В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Формула длины окружности , длина дуги окружности
где r—радиус окружности;
12. Формула площади круга
площадь кругового сектора где r—радиус круга.
ОСНОВНЫЕ ФАКТЫ по теме «ОКРУЖНОСТЬ и КРУГ»
Слайд 9Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите
угол, которые образуют две соседние спицы. Ответ дайте в градусах.
На
рисунке показано, как выглядит колесо с пятью спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 36 0 ?На рисунке показано, как выглядит колесо с 7 спицами. Найдите величину угла в градусах, который образуют две соседние спицы, если в колесе 45 спиц.
Сколько спиц в колесе, если угол между соседними спицами равен 90?
ЗАДАЧИ ПРО КОЛЕСО
(задание № 15, ОГЭ модуль «Геометрия»)
30 0
40
10
8 0
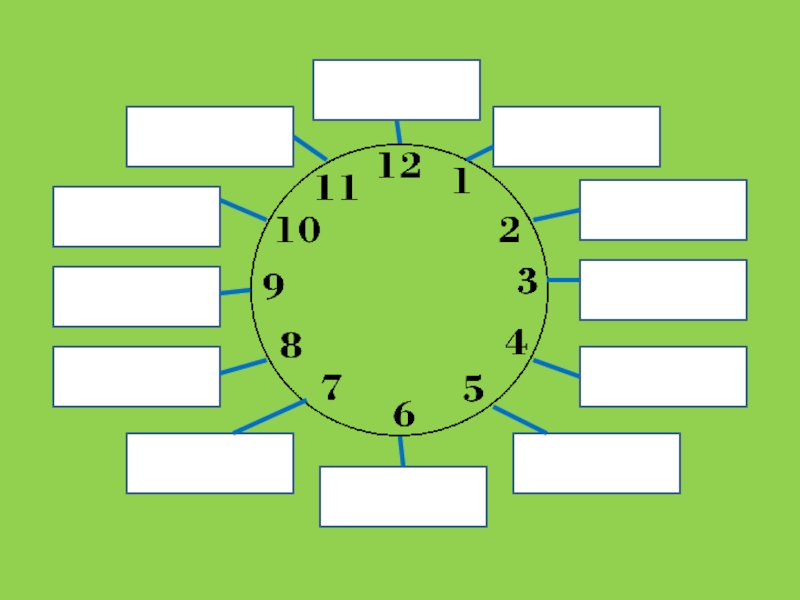
Слайд 10ЗАДАЧИ ПРО ЧАСЫ
(задание № 15, ОГЭ модуль «Геометрия»)
Найдите угол, который
образуют минутная и часовая стрелки часов в 18:00. Ответ дайте
в градусах.Найдите угол, который минутная стрелка описывает за 25 минут. Ответ дайте в градусах.
Какой угол в градусах описывает часовая стрелка за 4 часа?
Найдите угол, который образуют минутная и часовая стрелки часов в 14:00. Ответ дайте в градусах.
180 0
60 0
150 0
120 0
Слайд 12Дуга окружности, соответствующая центральному углу
это часть окружности, расположенная внутри угла
Градусная
мера дуги окружности
А
В
= АОВ
О
равна градусной мере
соответствующего ей
центрального угла.Слайд 13Вписанный угол
Это угол, вершина которого лежит на окружности, а стороны
пересекают окружность.
С
А
В
Слайд 14Теорема о вписанном угле
Угол, вписанный в окружность, равен половине соответствующего
ему центрального угла.
Угол, вписанный в окружность, равен половине дуги, на
которую он опирается.С
А
В
О
АСВ = ½ АОВ
АСВ = ½
Слайд 23Сейчас нельзя сказать, кто именно изобрел этот инструмент - история
не сохранила для нас его имя, но легенды Древней Греции
приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности, который вместе со своим сыном Икаром поднялся в небо на крыльях собственного изготовления. Вероятно, унаследовав от дяди дар изобретательства, Талос соединил два одинаковых по длине стержня и смастерил устройство способное чертить идеальный круг.Циркуль и линейка – самые старые чертёжные инструменты на Земле. На стенах и куполах храмов и домов, на резных чашах и кубках древних вавилонян и ассирийцев нарисованы такие правильные круги, что без циркуля их не провести. А существовали эти государства около 3-х тысяч лет назад.
Самый старый железный циркуль обнаружен во Франции при раскопках древнего кургана. Он пролежал в земле более 2-х тысяч лет.
В пепле, засыпавшем греческий город Помпеи, археологи обнаружили очень много бронзовых циркулей.
Слайд 25ВПИСАННАЯ ОКРУЖНОСТЬ
А
В
С
D
F
О
Если все стороны многоугольника касаются окружности, то окружность называется
вписанной в многоугольник, а многоугольник – описанным около этой окружности
На
каком рисунке окружность вписана в трапецию? Рис.1
Рис.2
Рис.3
Рис.4
Слайд 26ЗАМЕЧАНИЯ
В треугольник можно вписать
только одну окружность
2) Не
во всякий четырехугольник можно вписать окружность
В любой треугольник можно вписать
окружностьЦентр окружности, вписанной в треугольник, –
точка пересечения биссектрис.
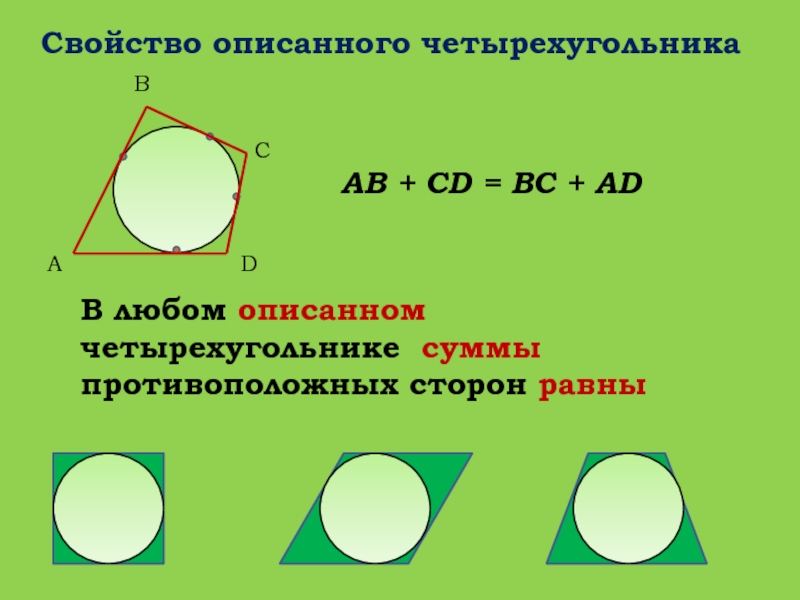
Слайд 27Свойство описанного четырехугольника
В любом описанном четырехугольнике суммы противоположных сторон
равны
A
B
C
D
AB + CD = BC + AD
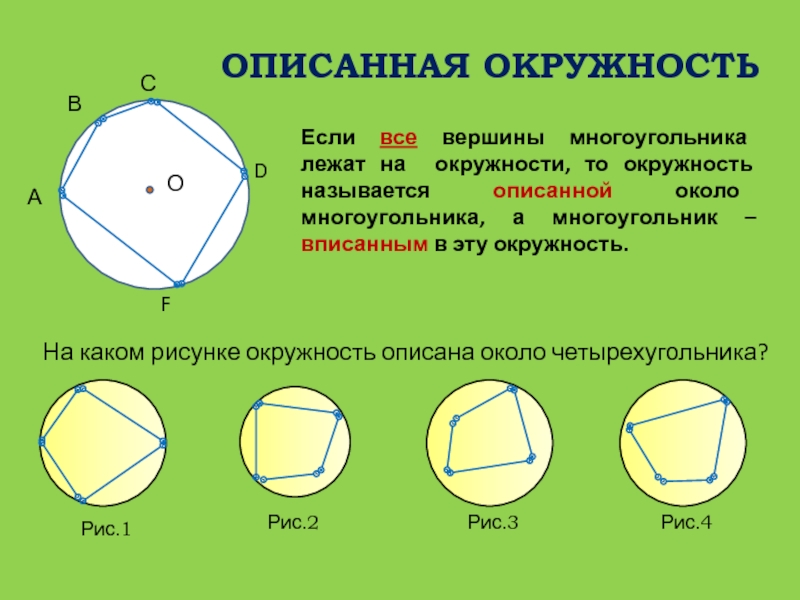
Слайд 28ОПИСАННАЯ ОКРУЖНОСТЬ
А
В
С
D
F
О
Если все вершины многоугольника лежат на окружности, то окружность
называется описанной около многоугольника, а многоугольник – вписанным в эту
окружность.На каком рисунке окружность описана около четырехугольника?
Рис.1
Рис.2
Рис.3
Рис.4
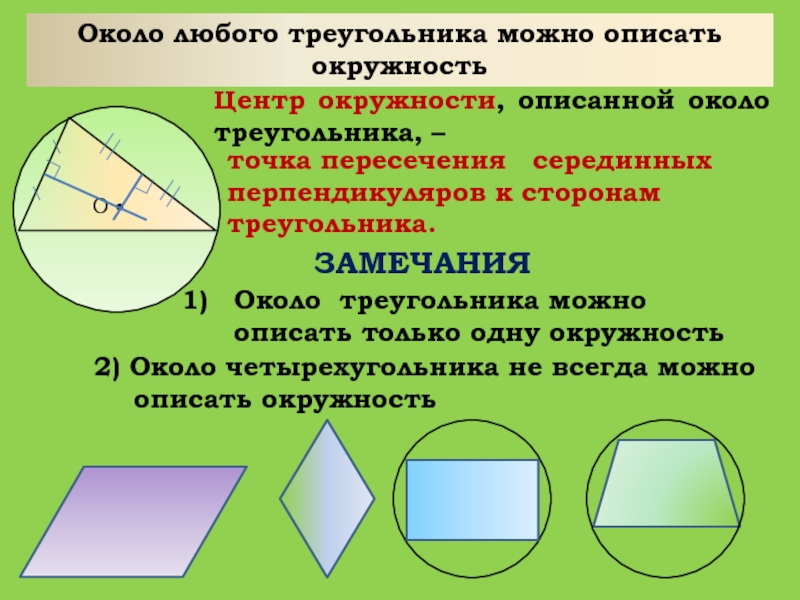
Слайд 29ЗАМЕЧАНИЯ
Около треугольника можно описать только одну окружность
2) Около четырехугольника не всегда можно описать
окружностьОколо любого треугольника можно описать окружность
Центр окружности, описанной около треугольника, –
точка пересечения серединных
перпендикуляров к сторонам треугольника.
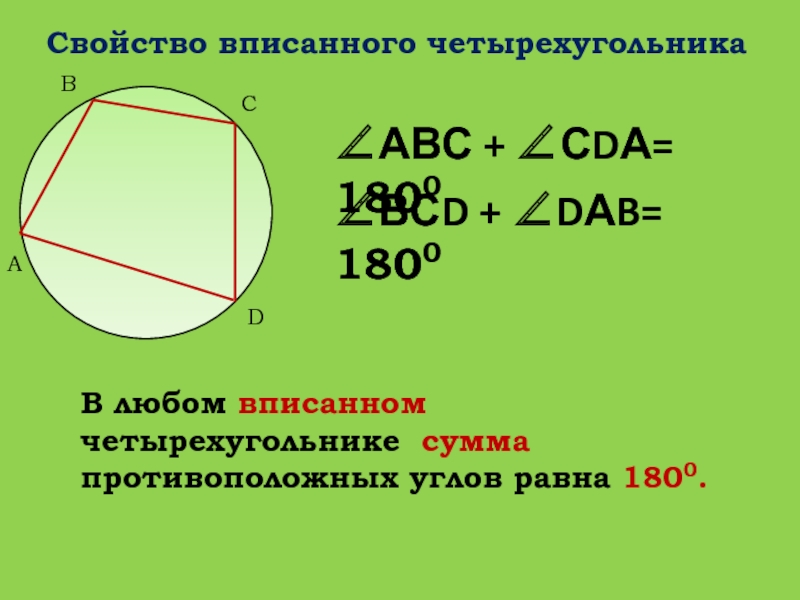
Слайд 30Свойство вписанного четырехугольника
В любом вписанном четырехугольнике сумма противоположных углов
равна 1800.
A
B
C
D
АВС + СDА= 1800
ВСD + DАB= 1800
Слайд 31Задача 1.
А
В
С
D
А
В
С
D
В четырёхугольнике АВСD АВ = 6, ВС = 9,
СD = 14. Найдите АD, если известно, что в четырёх-угольник
АВСD можно вписать окружность.Четырёхугольник АВСD вписан в окружность. Известно, что угол В равен 85° , угол А меньше угла D на 200. Найдите угол С.
Задача 2.
Ответ: АD =11
Ответ: угол С равен 1050
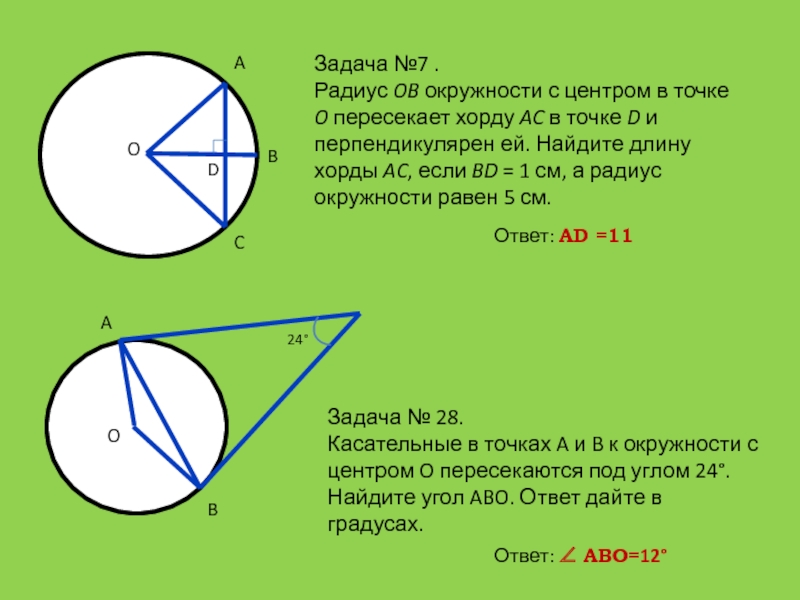
Слайд 32Задача №7 .
Радиус OB окружности с центром в точке O
пересекает хорду AC в точке D и перпендикулярен ей. Найдите
длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.Задача № 28.
Касательные в точках A и B к окружности с центром O пересекаются под углом 24°. Найдите угол ABO. Ответ дайте в градусах.
24°
Ответ: АD =11
Ответ: АВО=12°
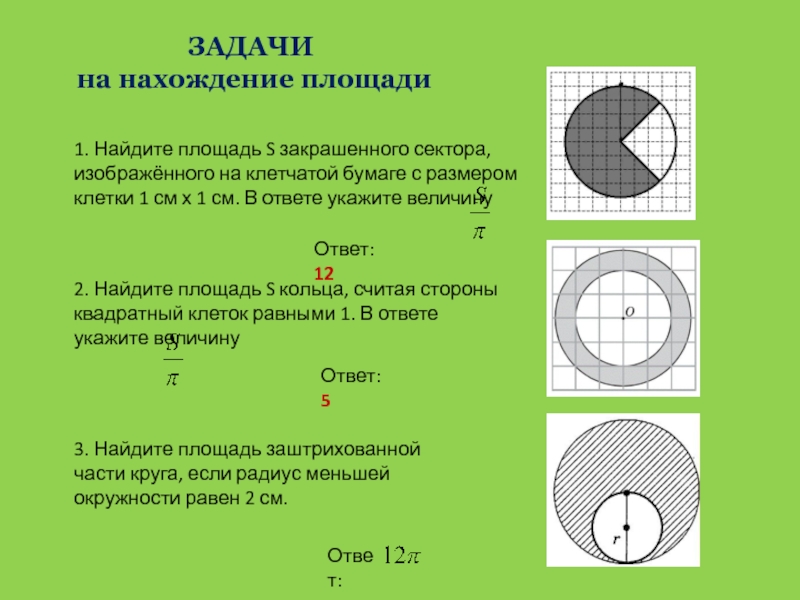
Слайд 33ЗАДАЧИ
на нахождение площади
1. Найдите площадь S закрашенного сектора, изображённого
на клетчатой бумаге с размером клетки 1 см х 1
см. В ответе укажите величину2. Найдите площадь S кольца, считая стороны квадратный клеток равными 1. В ответе укажите величину
3. Найдите площадь заштрихованной части круга, если радиус меньшей окружности равен 2 см.
Ответ:
Ответ: 5
Ответ: 12
Слайд 34 Выберите номера верных утверждений.
1). Величина дуги окружности равна величине вписанного угла,
на неё опирающегося.
2). Если в четырехугольник можно вписать окружность, то
суммы его противоположных сторон равны.3). Окружность симметрична относительно любого своего диаметра.
Выберите номера неверных утверждений.
1). Центр окружности, вписанной в треугольник,- это точка пересечения высот.
2). Угол, вершина которого лежит в центре окружности, называется вписанным.
3). Серединный перпендикуляр к хорде проходит через центр окружности.
Ответ: 2 3
Ответ: 1 2
Выберите номера верных утверждений.
1). Радиус окружности в два раза меньше диаметра.
2). Прямая , имеющая с окружностью две общие точки,- касательная.
3). Центры вписанной и описанной окружности равностороннего треугольника совпадают.
Ответ: 1 3
Слайд 35Домашнее задание:
1) Три задачи на выбор по карточкам «Задания для
подготовки к ОГЭ на готовых чертежах».
2) По сборникам типовых вариантов
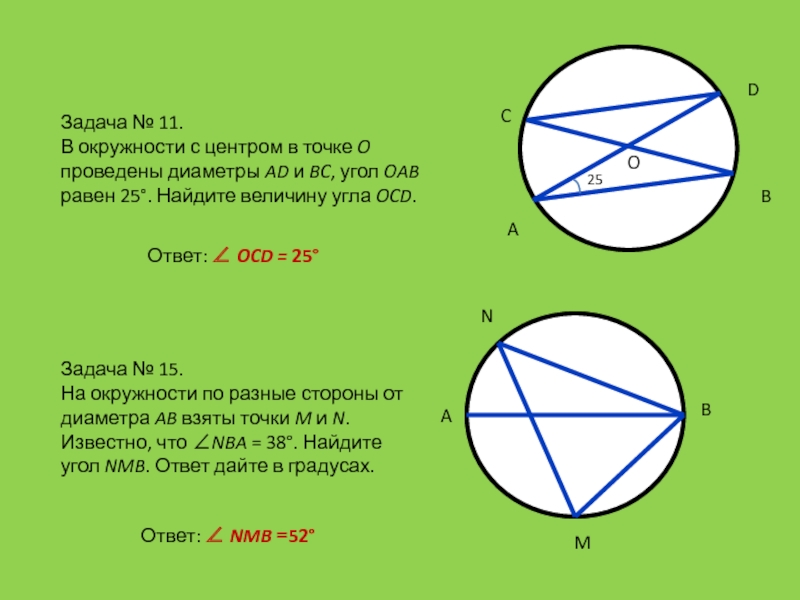
ОГЭ решать задания №17.Слайд 37Задача № 11.
В окружности с центром в точке O проведены
диаметры AD и BC, угол OAB равен 25°. Найдите величину
угла OCD.Задача № 15.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
A
B
M
N
Ответ: OCD = 25°
Ответ: NMB =52°