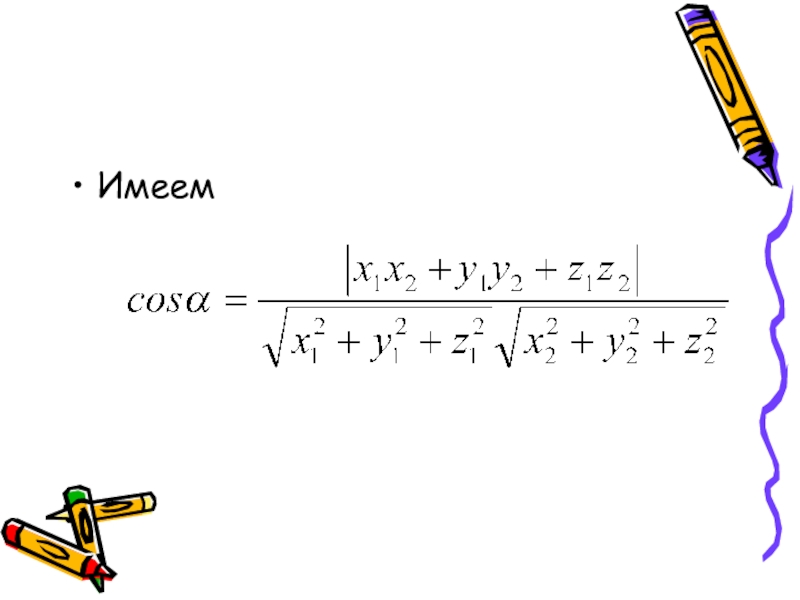Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между прямыми 11 класс
Содержание
- 1. Угол между прямыми 11 класс
- 2. Найдите координаты вектора A(1;-2;3), В(2;4;-1)
- 3. Найдите длину вектора
- 4. Найдите скалярное произведение векторов и
- 5. Дан куб с ребром, равным 1. Найдите скалярное произведение векторов и АВСDA1B1C1D1
- 6. Найдите скалярное произведение векторов если
- 7. Найдите длину вектора
- 8. Ненулевой вектор называется направляющим вектором прямой a,
- 9. Найти угол между двумя прямыми(пересекающимися или скрещивающимися),
- 10. Введем обозначение: Либо , если , либо , если .Поэтому либо либо , θ
- 11. Имеем
- 12. № 468 (а) Дано:
- 13. № Дано: -
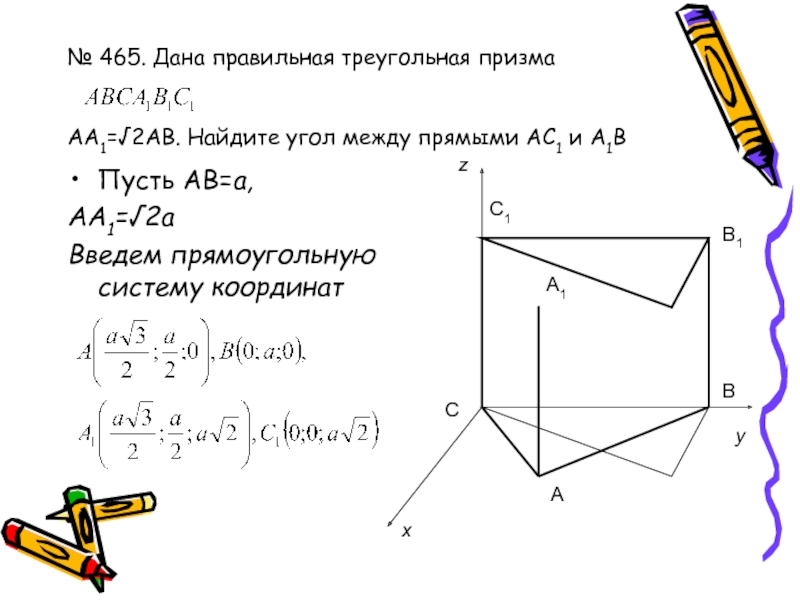
- 14. № 465. Дана правильная треугольная призма
- 15. № 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми АС1 и А1ВАВ1А1С1ВСxzy
- 16. № 465. Дана правильная треугольная призма
- 17. № 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми АС1 и А1ВАВ1А1С1ВСxzy
- 18. Самостоятельная работаВариант 1Дан кубНайдите угол между прямыми
- 19. Вариант1Ответ: 450Вариант2Ответ: 600
- 20. Домашнее заданиеП. 52 задача 1, №464(а), ;№ 465,№466(а)
- 21. Спасибо за урок
- 22. Скачать презентанцию
Найдите координаты вектора A(1;-2;3), В(2;4;-1)
Слайды и текст этой презентации
Слайд 8Ненулевой вектор называется направляющим вектором прямой a, если он либо
лежит на прямой a, либо на прямой, параллельной a.
Слайд 9Найти угол между двумя прямыми(пересекающимися или скрещивающимися), если известны координаты
направляющих векторов этих прямых
Пусть
направляющие векторы прямых a и b, α
– угол между этими прямыми.Найдем cos α
a
b
α
Слайд 12№ 468 (а) Дано: - прямоугольный
параллелепипед.
Вычислить угол между прямыми АС и D1B
Введем прямоугольную систему координат
в ней:А(1;0;0), С(0;2;0),
В(0;0;0), D1(1;2;3)
x
z
y
A
A1
C
B
D
D1
C1
B1
Слайд 13№ Дано: - прямоугольный параллелепипед. Вычислить угол
между прямыми АС и D1B
x
z
y
A
A1
C
B
D
D1
C1
B1
Слайд 14№ 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми
АС1 и А1В
Пусть АВ=a,
АА1=√2a
Введем прямоугольную систему координат
А
В1
А1
С1
В
С
x
z
y
Слайд 15№ 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми
АС1 и А1В
А
В1
А1
С1
В
С
x
z
y
Слайд 16№ 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми
АС1 и А1В
Векторы и
Являются направляющими векторами прямых АС1 и А1В
А
В1
А1
С1
В
С
x
z
y
Слайд 17№ 465. Дана правильная треугольная призма АА1=√2АВ. Найдите угол между прямыми
АС1 и А1В
А
В1
А1
С1
В
С
x
z
y
Слайд 18Самостоятельная работа
Вариант 1
Дан куб
Найдите угол между прямыми AD1 и ВК,
где К – середина DD1
Вариант 2
Дан куб
Найдите угол между прямыми
АС и DC1
