Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Золотое сечение
Содержание
- 1. Золотое сечение
- 2. Вот вы подходите к пустой скамейке и
- 3. Золотое сечение непосредственно связано с числами Фибоначчи,
- 4. Специальные названия этому соотношению начали давать еще
- 5. Так что же такое золотое сечение? Число
- 6. Золотое сечение в математике Золотое сечение –
- 7. Практическое знакомство с золотым сечением начинают с
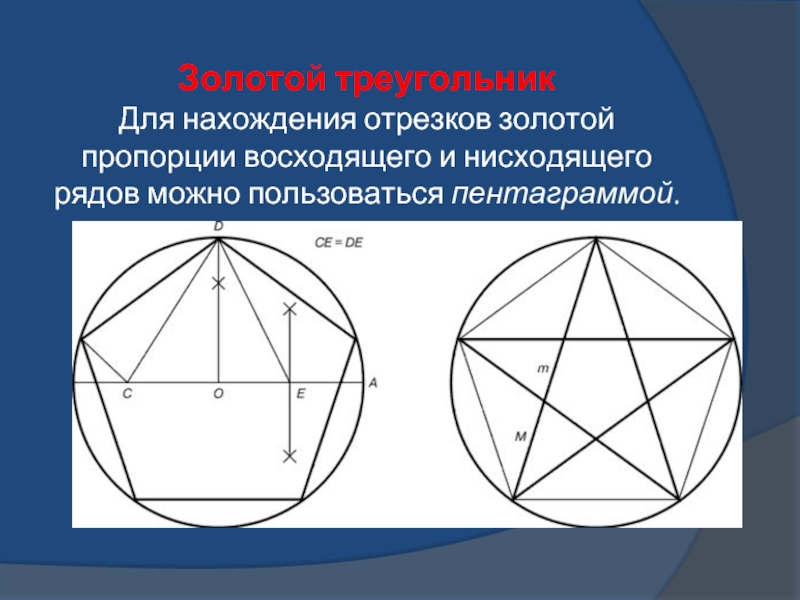
- 8. Золотой треугольник Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
- 9. Каждый конец пятиугольной звезды представляет собой золотой
- 10. Прямоугольник с таким отношением сторон стали называть
- 11. Слайд 11
- 12. Золотое сечение в частях тела Сопоставляя
- 13. Пропорции золотого сечения проявляются в отношении длины
- 14. Золотое сечение в скульптуре Золотая
- 15. Венера Милосская – шедевр античного искусства. Отношение
- 16. Еще в эпоху Возрождения художники открыли,
- 17. Золотое сечение в архитектуре Одним из красивейших
- 18. На рисунках виден целый ряд
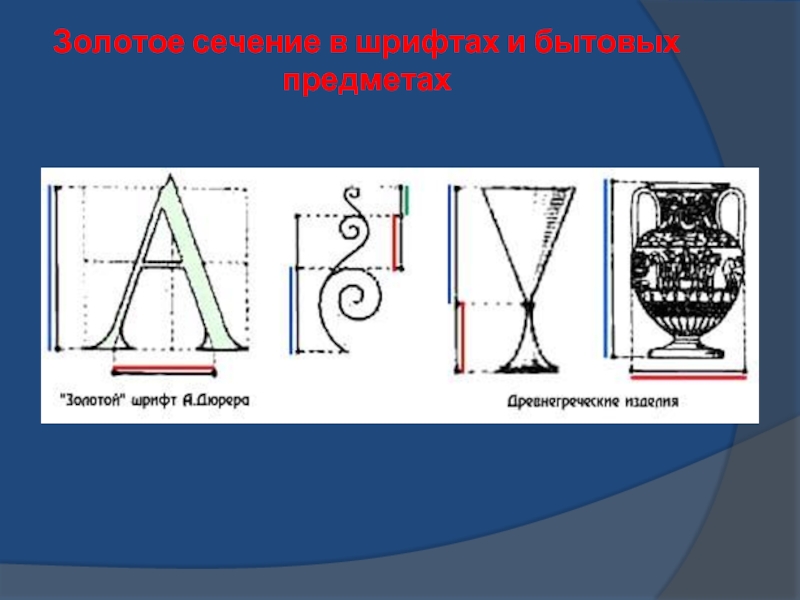
- 19. Золотое сечение в шрифтах и бытовых предметах
- 20. Золотое сечение в биологии Росток Среди придорожных
- 21. Все живое и все красивое —
- 22. История золотого сечения уходит в пласты тысячелетий.
- 23. Скачать презентанцию
Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не
Слайды и текст этой презентации
Слайд 2Вот вы подходите к пустой скамейке и садитесь на нее.
Где вы сядете — посередине? Или, может быть, с самого
края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62.Слайд 3Золотое сечение непосредственно связано с числами Фибоначчи, о которых впервые
было рассказано в научном трактате «Книга об абаке» итальянского ученого
Леонардо Фибоначчи, жившего в XIII веке. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. Числа, образующие последовательность 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …называются числами Фибоначчи. Каждый член этой последовательности, начиная с 3-го, равен сумме двух предыдущих членов. Если какое-либо число Фибоначчи разделить на предыдущее (например, 3:2, 5:3, 8:5 и т.д.), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875…Слайд 4Специальные названия этому соотношению начали давать еще до того, как
Лука Пачоли, средневековый математик, назвал его Божественной пропорцией. Среди его
современных названий есть такие, как «золотое сечение», «золотое среднее» и «отношение вертящихся квадратов». Кеплер назвал это соотношение одним из сокровищ геометрии.Слайд 5Так что же такое золотое сечение? Число 1.618 играет важную
роль как во многих разделах математики, так и в мире
искусств, где с античных времен оно рассматривалось как эстетически самое благоприятное отношение. Поэтому оно имеет специальное название - «отношение золотого сечения» - и обозначается греческой буквой Ф в честь Фидия, который, как утверждается, сознательно использовал его в своих скульптурах.Слайд 6Золотое сечение в математике Золотое сечение – это такое пропорциональное деление
отрезка на неравные части, при котором весь отрезок так относится
к большей части, как сама большая часть относится к меньшейСлайд 7Практическое знакомство с золотым сечением начинают с деления отрезка прямой
в золотой пропорции с помощью циркуля и линейки. Отрезки золотой пропорции
выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38. Свойства золотого сечения описываются уравнением: x2 – x – 1 = 0. Решение этого уравнения:Слайд 8Золотой треугольник Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов
можно пользоваться пентаграммой.
Слайд 9Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны
образуют угол 36° при вершине, а основание, отложенное на боковую
сторону, делит ее в пропорции золотого сечения.Слайд 10Прямоугольник с таким отношением сторон стали называть золотым прямоугольником .
Он также обладает интересными свойствами. Если от него отрезать квадрат,
то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности. Золотой прямоугольник можно использовать для построения золотой спирали – разновидности логарифмической спирали, часто встречающейся в природе: паук прядет свою паутину в виде такой спирали, в сосновых шишках, раковинах улиток и моллюсков, папоротниках, головках подсолнуха мы тоже увидим золотую спираль.Слайд 12 Золотое сечение в частях тела Сопоставляя длины фаланг пальцев и кисти
руки в целом, а также расстояния между отдельными частями лица,
также можно найти "золотые" соотношения: Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении золотого сечения. Измерения нескольких тысяч человеческих тел позволили обнаружить, что для взрослых мужчин это отношение равно в среднем примерно 13/8 = 1,625Слайд 13Пропорции золотого сечения проявляются в отношении длины плеча, предплечья, кисти
и пальцев. Поразительно, но в лице человека можно проследить множество
пропорций, подчиненных золото- которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к числу 1,618.Слайд 14 Золотое сечение в скульптуре Золотая пропорция применялась многими античными скульпторами. Известна
золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной
линией в золотом сечении.Слайд 15Венера Милосская – шедевр античного искусства. Отношение между расстоянием от
головы до стоп и от пупа до стоп равняется золотому
числу 1,618, так же как отношение длины головы к расстоянию между глазами и подбородком; или отношение расстояния от носа до подбородка к расстоянию между губами и подбородкомСлайд 16 Еще в эпоху Возрождения художники открыли, что любая картина имеет
определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры.
При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости.