TheSlide.ru

Площадь криволинейной трапеции и интеграл

Содержание

1. Площадь криволинейной трапеции и интеграл
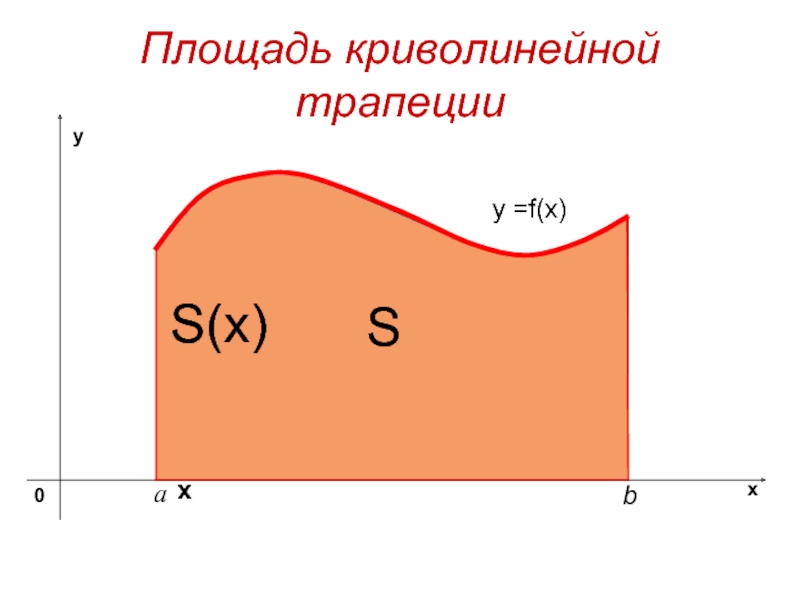
2. Площадь криволинейной трапецииy =f(x) SхS(x)
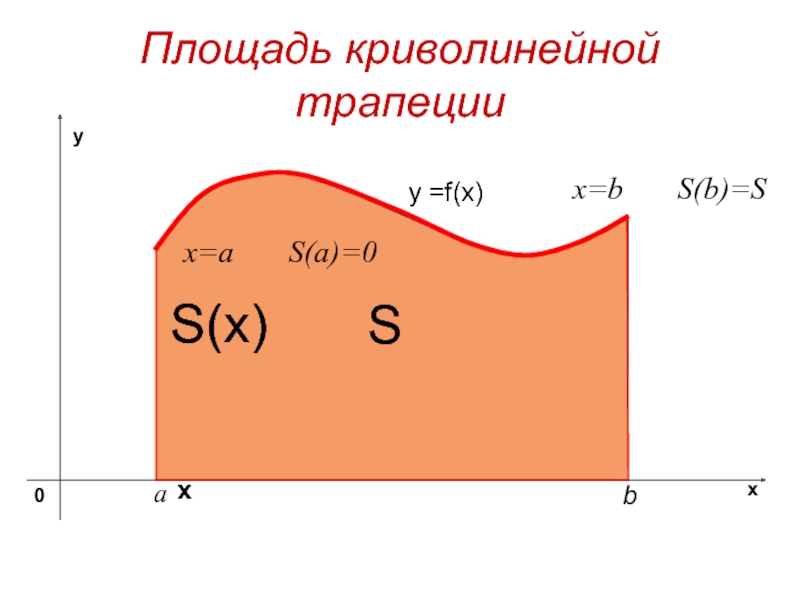
3. Площадь криволинейной трапецииy =f(x) SхS(x)x=a S(a)=0x=b S(b)=S
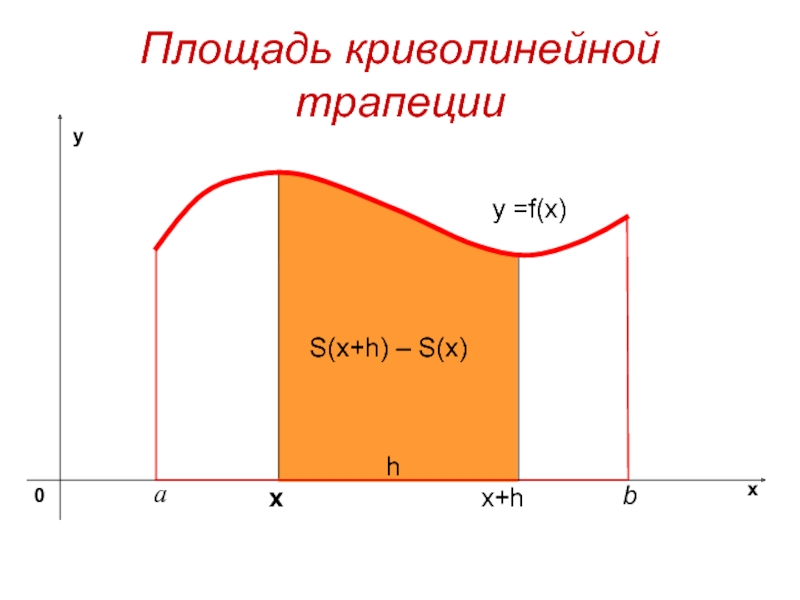
4. Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hh
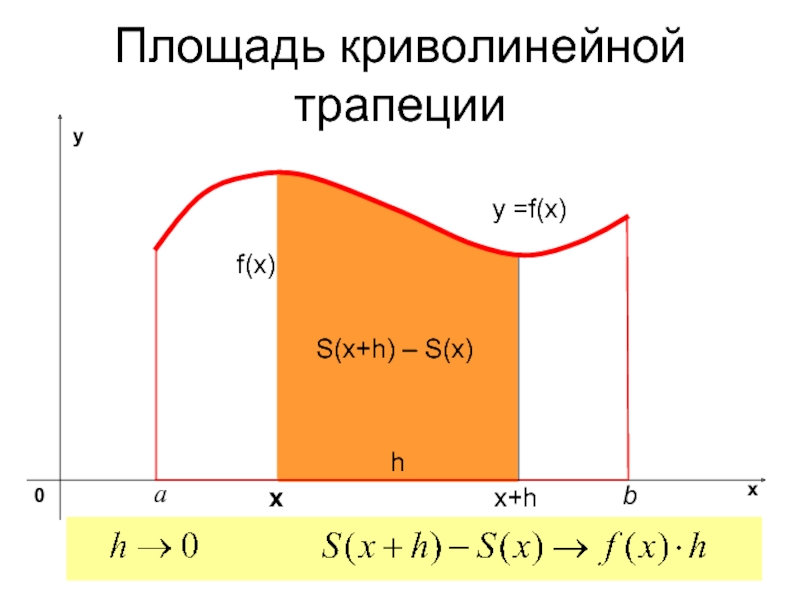
5. Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hhf(x)
6. Площадь криволинейной трапеции
7. Фигура, ограниченная снизу отрезком [a, b]
8. Обозначим S(х) - площадь криволинейной трапеции с
9. S(х) является первообразной функции f(x), т.е. S'(х)= f(x)
10. Площадь криволинейной трапеции
11. Любая другая первообразная F(x) отличается от
12. Немного истории -1675 г, опубликовано в 1686
13. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
14. Исаак Ньютон (1643-1727)Разумом он превосходил род человеческий.
15. Немного истории «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer
16. интегральное исчисление неопределенный интеграл определенный интеграл (первообразная) (площадь криволинейной фигуры) И.Ньютон Г.Лейбниц
17. Применение интеграла Площадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыЦентр масс
18. В классе:№ 999(1,3)№ 1000(1,2)
19. Дома:П 56№ 999(2,4)№ 1000(3)
20. Скачать презентанцию

Площадь криволинейной трапецииy =f(x) SхS(x)

Главная
Геометрия
Площадь криволинейной трапеции и интеграл

Слайды и текст этой презентации

Слайд 1Площадь криволинейной трапеции и интеграл.

Площадь криволинейной трапеции и интеграл.

Слайд 2Площадь криволинейной трапеции

y =f(x)
S
х
S(x)

Площадь криволинейной трапецииy =f(x) SхS(x)

Слайд 3Площадь криволинейной трапеции

y =f(x)
S
х
S(x)
x=a S(a)=0
x=b

S(b)=S

Площадь криволинейной трапецииy =f(x) SхS(x)x=a S(a)=0x=b S(b)=S

Слайд 4Площадь криволинейной трапеции

y =f(x)
х
S(x+h) – S(x)
x+h
h

Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hh

Слайд 5Площадь криволинейной трапеции

y =f(x)
х
S(x+h) – S(x)
x+h

h
f(x)

Площадь криволинейной трапецииy =f(x) хS(x+h) – S(x)x+hhf(x)

Слайд 6
Площадь криволинейной трапеции

Площадь криволинейной трапеции

Слайд 7 Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху

графиком непрерывной функции у= f(x), принимающей положительные значения , а

с боков отрезками прямых х = а, х =b называется криволинейной трапецией.

Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные

Слайд 8Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х]

,
х - любая точка отрезка [a, b]

При х = а отрезок [a, х] вырождается в
точку, поэтому S(а) = 0; при х = b,
S(b) = S

Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] , х - любая точка отрезка [a,

Слайд 9 S(х) является первообразной функции f(x), т.е.

S'(х)= f(x)

S(х) является первообразной функции f(x), т.е. S'(х)= f(x)

Слайд 10 Площадь криволинейной трапеции вычисляется по

формуле S = F(b) - F(a)
Разность F(b)

- F(a) называют
интегралом от функции f(x)
на отрезке [a, b] и обозначают так :

Площадь криволинейной трапеции вычисляется по формуле S

Слайд 11Любая другая первообразная F(x) отличается от S(x) на постоянную, т.е.

F(x) = S(x) + С
При х = а получаем F(a)

= S(a) + C
Так как S(a) = 0 , то С = F(a) и равенство
F(x) = S(x) + С можно записать так
S(x) = F(x) - F(a), отсюда при х =b получим
S(b) = F(b) - F(a)

Любая другая первообразная F(x) отличается от S(x) на постоянную, т.е. F(x) = S(x) + С

Слайд 12Немного истории

-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц

- 1675 г,

Ж Лагранж
5 век до н.э. др.гр. ученый Демокрит
3-4 век до

н.э. Архимед ввел метод исчерпывания

Немного истории -1675 г, опубликовано в 1686 гввел Г.Лейбниц- 1675 г, Ж Лагранж5 век до н.э. др.гр.

Слайд 13Лейбниц Готфрид Вильгельм (1646-1716)
« Общее искусство знаков представляет чудесное

пособие, так как оно разгружает воображение… Следует заботиться о том,

чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»
Лейбниц

Лейбниц Готфрид Вильгельм (1646-1716) « Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение…

Слайд 14Исаак Ньютон (1643-1727)
Разумом он превосходил род человеческий.

Лукреций

Исаак Ньютон (1643-1727)Разумом он превосходил род человеческий. Лукреций

Слайд 15Немного истории
«Интеграл» придумал Я.Бернулли (1690)
«восстанавливать» от латинского integro
«целый» от латинского

integer

Немного истории «Интеграл» придумал Я.Бернулли (1690)«восстанавливать» от латинского integro«целый» от латинского integer

Слайд 16интегральное исчисление
неопределенный интеграл
определенный интеграл
(первообразная)
(площадь криволинейной фигуры)

И.Ньютон
Г.Лейбниц

интегральное исчисление неопределенный интеграл определенный интеграл (первообразная) (площадь криволинейной фигуры) И.Ньютон Г.Лейбниц

Слайд 17Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Центр

масс

Применение интеграла Площадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыЦентр масс

Слайд 18В классе:
№ 999(1,3)
№ 1000(1,2)

В классе:№ 999(1,3)№ 1000(1,2)

Слайд 19Дома:
П 56
№ 999(2,4)
№ 1000(3)

Дома:П 56№ 999(2,4)№ 1000(3)

Скачать презентацию

Теги

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей