Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач по теме "Четырехугольники"
Содержание
- 1. Решение задач по теме "Четырехугольники"
- 2. Задачипо теме четырехугольники
- 3. ПрямоугольникПараллелограмм, у которого все углы прямые, называется прямоугольником.
- 4. ПризнакЕсли в параллелограмме диагонали равны, то этот
- 5. КвадратПрямоугольник, у которого все стороны равны, называется
- 6. СвойстваВсе углы квадрата прямые. (рис.1)ABCDДоказательство.Прямоугольник является параллелограммом,
- 7. РомбПараллелограмм, у которого все стороны равны, называется ромбом.
- 8. СвойстваДиагонали ромба взаимно перпендикулярны и делят его
- 9. ЗадачиABCD – прямоугольник.ВСDА1.Доказать: BN=CM.MNВСDА3.OEДано: ОЕ= 4.Найти: АС.60˚ВСDА2.O55˚Найти: ﮮCOD; ﮮACD.ВСDА4.А1B1C1D1C1D1Доказать: A1B1C1D1 - ромб.
- 10. ЗадачиABCD – ромб.ВСDА5.50˚Найти: ﮮBDC.7.ВСDАНайти: ﮮBАD.55˚6.ВСDАНайти: ﮮABC.75˚8.ВСDАЕ20˚Найти: ﮮBАD.
- 11. ЗадачиABCD – ромб.9.ВСDАДоказать: BM = BN.NM10.ВСDАEFДоказать: BE = DF.11.12.ABCDОДоказать: OK = OP.KPCBDAKДоказать: КВ = КD.О
- 12. Ответы1. a) ﮮABN= ﮮNBC=45˚, т. к.
- 13. Упражнение 1Из точки D, принадлежащей гипотенузе AB
- 14. Упражнение 2Два равных прямоугольных треугольника приложили один
- 15. Упражнение 3Меньшая сторона прямоугольника равна 5 см, диагонали пересекаются под углом 60о. Найдите диагонали прямоугольника.
- 16. Упражнение 4В прямоугольнике диагональ делит угол в
- 17. Упражнение 5Диагональ прямоугольника вдвое больше одной из
- 18. Упражнение 6Тупой угол между диагоналями прямоугольника равен
- 19. Упражнение 7Существует ли четырехугольник, не являющийся прямоугольником, диагонали которого были бы равны?
- 20. Упражнение 8Верно ли утверждение о том, что
- 21. Упражнение 9В прямоугольном треугольнике ABC из вершины
- 22. Упражнение 10Найдите диагонали прямоугольника, если его периметр
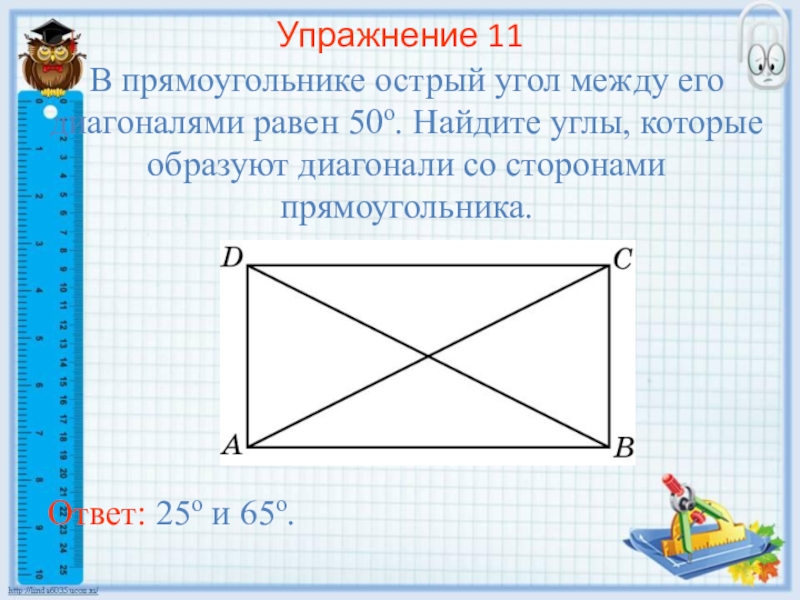
- 23. Упражнение 11В прямоугольнике острый угол между его
- 24. Упражнение 12Перпендикуляр BH, опущенный из вершины B
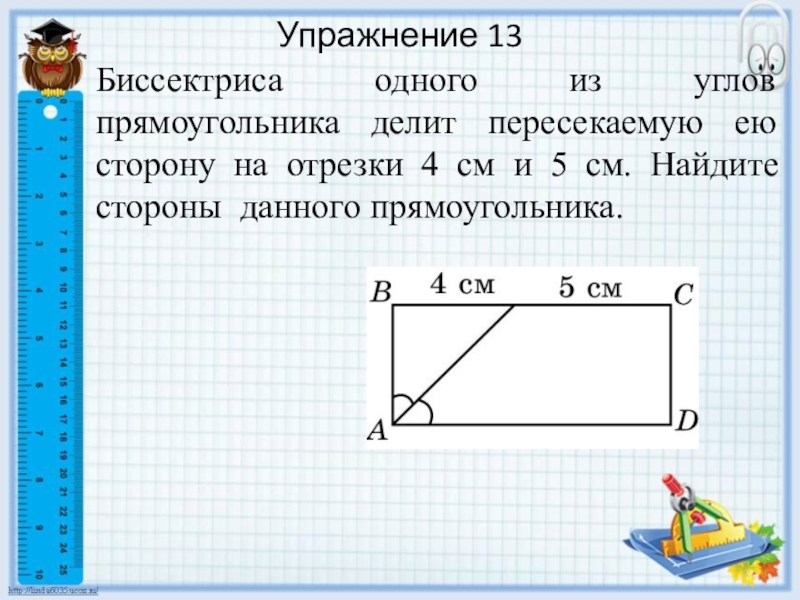
- 25. Упражнение 13Биссектриса одного из углов прямоугольника делит
- 26. Упражнение 14Чему равна меньшая диагональ ромба со стороной а и острым углом в 60о?
- 27. Упражнение 15В ромбе одна из диагоналей равна его стороне. Найдите углы ромба.
- 28. Упражнение 16Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба.
- 29. Упражнение 17Чему равен угол между: а) диагоналями квадрата: б) диагональю и стороной квадрата?
- 30. Упражнение 18В квадрате расстояние от точки пересечения
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Признак
Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.
A
B
C
D
AC=BD
Доказательство.
Треугольники
ABD и DCA равны по трем сторонам (AB=DC, BD=CA, AD
– общая сторона). Отсюда следует, что ﮮА = ﮮD. Так как в параллелограмме противоположные углы равны, то ﮮА = ﮮС и ﮮB = ﮮ D. Таким образом, ﮮ А = ﮮВ = ﮮС = ﮮD. Параллелограмм – выпуклый четырехугольник, поэтому ﮮА+ ﮮB+ ﮮС+ ﮮD = 360˚. Следовательно,ﮮA= ﮮB= ﮮC= ﮮD=90˚, то есть параллелограмм ABCD является прямоугольником.
Слайд 5Квадрат
Прямоугольник, у которого все стороны равны, называется квадратом.
Можно сказать,
что квадратом является ромб, у которого все углы прямые.
Слайд 6Свойства
Все углы квадрата прямые. (рис.1)
A
B
C
D
Доказательство.
Прямоугольник является параллелограммом, поэтому и квадрат
является параллелограммом, у которого все стороны равны, то есть ромбом.
Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба.2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам, делят углы квадрата пополам. (рис.2)
A
B
C
D
Рис.1
Рис.2
O
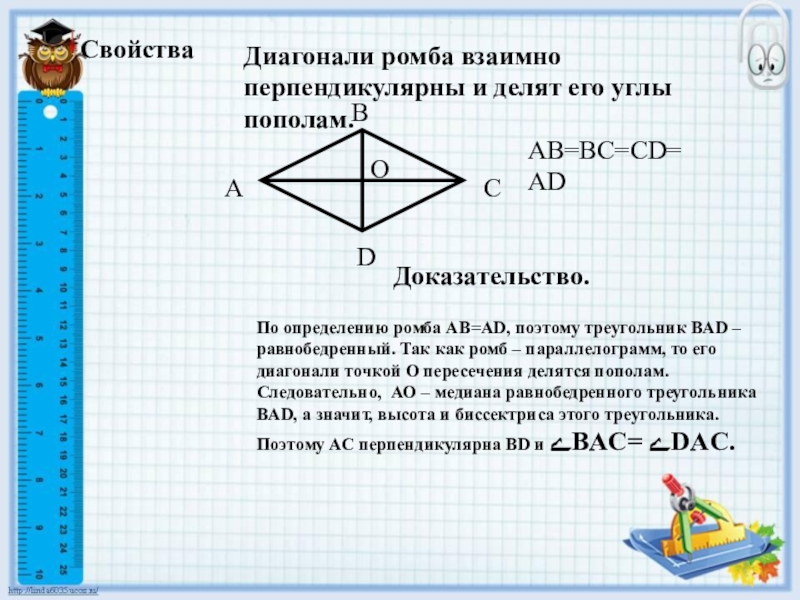
Слайд 8Свойства
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
A
B
C
D
AB=BC=CD=AD
Доказательство.
О
По определению
ромба AB=AD, поэтому треугольник BAD – равнобедренный. Так как ромб
– параллелограмм, то его диагонали точкой О пересечения делятся пополам. Следовательно, АО – медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому АС перпендикулярна BD и ﮮBAC= ﮮDAC.Слайд 9Задачи
ABCD – прямоугольник.
В
С
D
А
1.
Доказать: BN=CM.
M
N
В
С
D
А
3.
O
E
Дано: ОЕ= 4.
Найти: АС.
60˚
В
С
D
А
2.
O
55˚
Найти: ﮮCOD; ﮮACD.
В
С
D
А
4.
А1
B1
C1
D1
C1
D1
Доказать: A1B1C1D1
- ромб.
Слайд 10Задачи
ABCD – ромб.
В
С
D
А
5.
50˚
Найти: ﮮBDC.
7.
В
С
D
А
Найти: ﮮBАD.
55˚
6.
В
С
D
А
Найти: ﮮABC.
75˚
8.
В
С
D
А
Е
20˚
Найти: ﮮBАD.
Слайд 11Задачи
ABCD – ромб.
9.
В
С
D
А
Доказать: BM = BN.
N
M
10.
В
С
D
А
E
F
Доказать: BE = DF.
11.
12.
A
B
C
D
О
Доказать: OK
= OP.
K
P
C
B
D
A
K
Доказать: КВ = КD.
О
Слайд 12Ответы
1. a) ﮮABN= ﮮNBC=45˚, т. к. ﮮABC=90˚.
b) ﮮВСM= ﮮMСD=45˚, т. к. ﮮBCD=90˚.
=> ﮮABN= ﮮMCD
c)Треугольник ABN = DCM (AB=CD, ﮮA= ﮮB=90˚, ﮮABN= ﮮMCD); Следовательно, BN=CM.
2. a) ﮮACB=180˚-90 ˚-55 ˚=35 ˚(ABC – прямоугольный треугольник); b) ﮮСOD=180 ˚-55 ˚-55 ˚=70 ˚ (BOA – равнобедренный треугольник).
3. Из треугольника BOE (ﮮE=90 ˚, ﮮB=30 ˚) OB=2OE=8, BD=2OB=16. AC=BD=16.
4. Прямоугольные треугольники A1BB1, B1CC1, C1DD1,D1AA1 равны (A1B=CC1=C1D=AA1, BB1=B1C=DD1=D1A). Следовательно, A1B1=B1C1=C1D1=D1A1, т.е. A1B1C1D1 – ромб.
5. ﮮBDC=(180˚-50 ˚)/2=75 ˚(треугольник BCD равнобедренный).
6. ﮮABC= ﮮADC=180˚-75˚=105˚ (т.к. ﮮABC и ﮮADCпротиволежащие).
7. ﮮBAD=180˚-55˚-55˚=70˚ (равнобедренные треугольники АBD = BCD)
8. ﮮBDC=180˚-90˚-20˚=70˚; ﮮBСD=180˚-70˚-70˚=40˚= ﮮBAD.
Прямоугольные треугольники ABM и NBC равны (AB=BC, ﮮA= ﮮC), => BM=BN.
10. Прямоугольные треугольники ADF и ABE равны (AB=AD, ﮮA – общий)=>BE=DF.
11. Прямоугольные треугольники OKC и OPC равны (OC - общая, ﮮDCO=ﮮBCO)=>OK=OP.
12. Прямоугольные треугольники KBO и KDO равны (KO - общая, BO=OD) => KB=KD.
Слайд 13Упражнение 1
Из точки D, принадлежащей гипотенузе AB прямоугольного треугольника ABC,
проведены две прямые, параллельные катетам. Сумма периметров получившихся треугольников AKD
и DLB равна 10 см. Найдите периметр данного треугольника ABC.Слайд 14Упражнение 2
Два равных прямоугольных треугольника приложили один к другому таким
образом, что их гипотенузы совпали, а неравные острые углы приложились
один к другому. Какой при этом получился четырехугольник?Слайд 15Упражнение 3
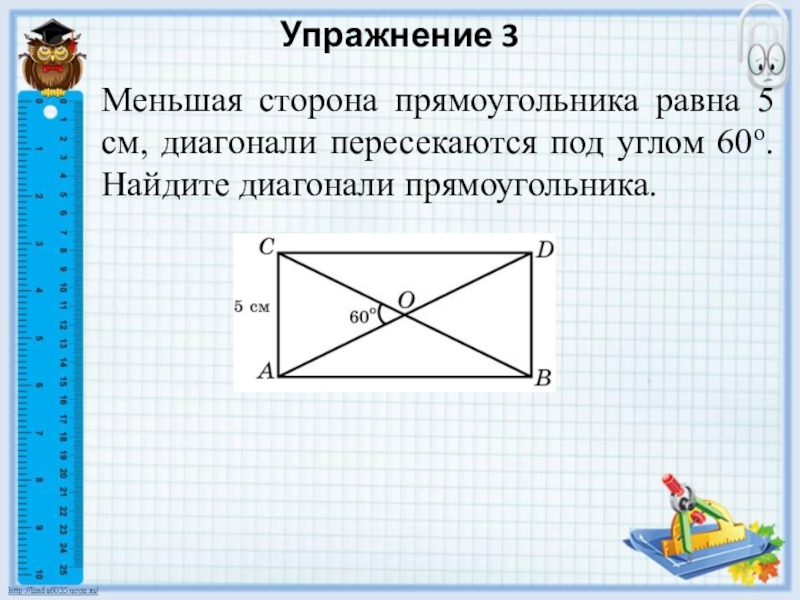
Меньшая сторона прямоугольника равна 5 см, диагонали пересекаются под
углом 60о. Найдите диагонали прямоугольника.
Слайд 16Упражнение 4
В прямоугольнике диагональ делит угол в отношении 1:2, меньшая
его сторона равна 5 см.Найдите диагонали данного прямоугольника.
Слайд 17Упражнение 5
Диагональ прямоугольника вдвое больше одной из его сторон. Какие
углы образуют диагонали со сторонами прямоугольника?
Слайд 18Упражнение 6
Тупой угол между диагоналями прямоугольника равен 120°. Чему при
этом будет равно отношение его меньшей стороны к диагонали?
Слайд 19Упражнение 7
Существует ли четырехугольник, не являющийся прямоугольником, диагонали которого были
бы равны?
Слайд 20Упражнение 8
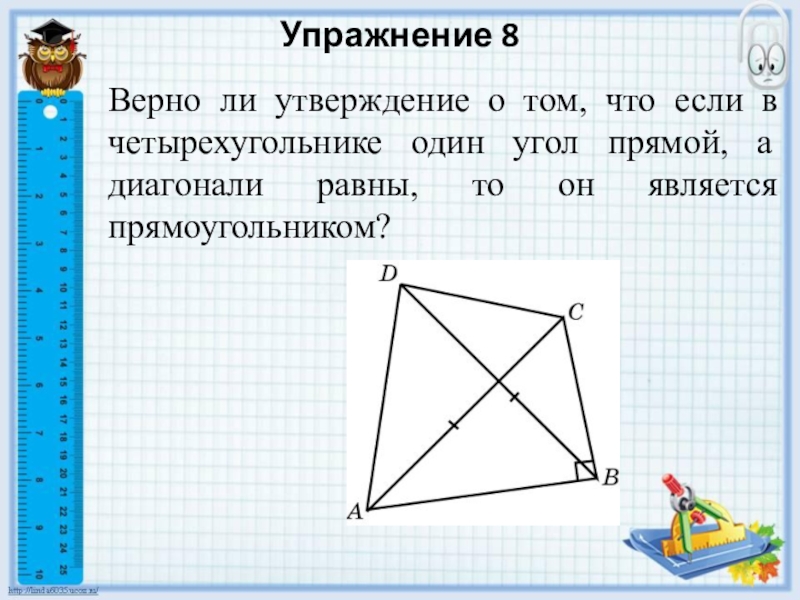
Верно ли утверждение о том, что если в четырехугольнике
один угол прямой, а диагонали равны, то он является прямоугольником?
Слайд 21Упражнение 9
В прямоугольном треугольнике ABC из вершины прямого угла C
опущена высота CH, равная 3 см. Из точки H опущены
перпендикуляры HK и HL на катеты треугольника. Найдите расстояние между точками K и L.Слайд 22Упражнение 10
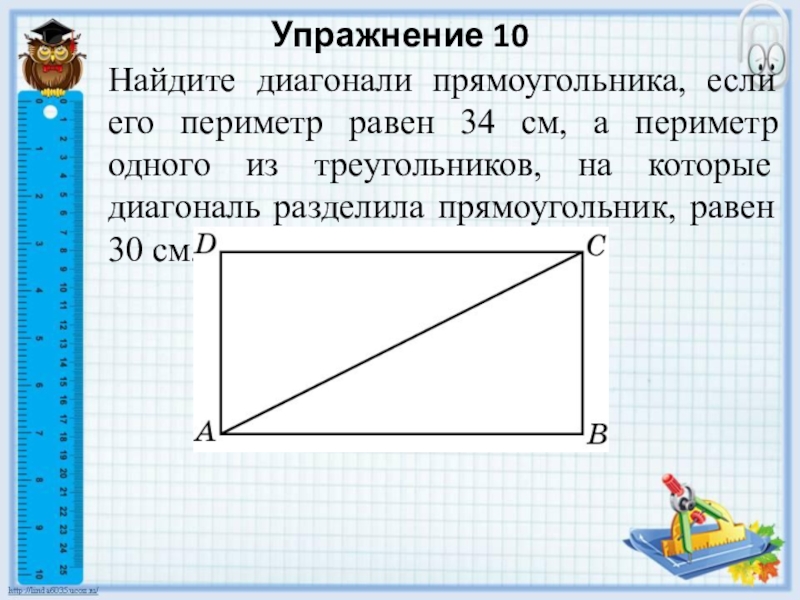
Найдите диагонали прямоугольника, если его периметр равен 34 см,
а периметр одного из треугольников, на которые диагональ разделила прямоугольник,
равен 30 см.Слайд 23Упражнение 11
В прямоугольнике острый угол между его диагоналями равен 50о.
Найдите углы, которые образуют диагонали со сторонами прямоугольника.
Ответ: 25о и
65о.Слайд 24Упражнение 12
Перпендикуляр BH, опущенный из вершины B прямоугольника ABCD на
его диагональ AC, делит угол B в отношении 2:3. Найдите:
а) углы, которые образуют диагонали данного прямоугольника с его сторонами; б) угол между перпендикуляром BH и диагональю BD.Слайд 25Упражнение 13
Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону
на отрезки 4 см и 5 см. Найдите стороны данного
прямоугольника.Слайд 28Упражнение 16
Углы, образуемые диагоналями ромба с одной из его сторон,
относятся как 4:5. Найдите углы ромба.
Слайд 29Упражнение 17
Чему равен угол между: а) диагоналями квадрата: б) диагональю
и стороной квадрата?
Слайд 30Упражнение 18
В квадрате расстояние от точки пересечения диагоналей до одной
из его сторон равно 5 см. Найдите периметр этого квадрата.