Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве
Содержание
- 1. Векторы в пространстве
- 2. Понятие вектора Многие физические величины, например
- 3. Электрическое поле, создаваемое в пространстве зарядами, характеризуется
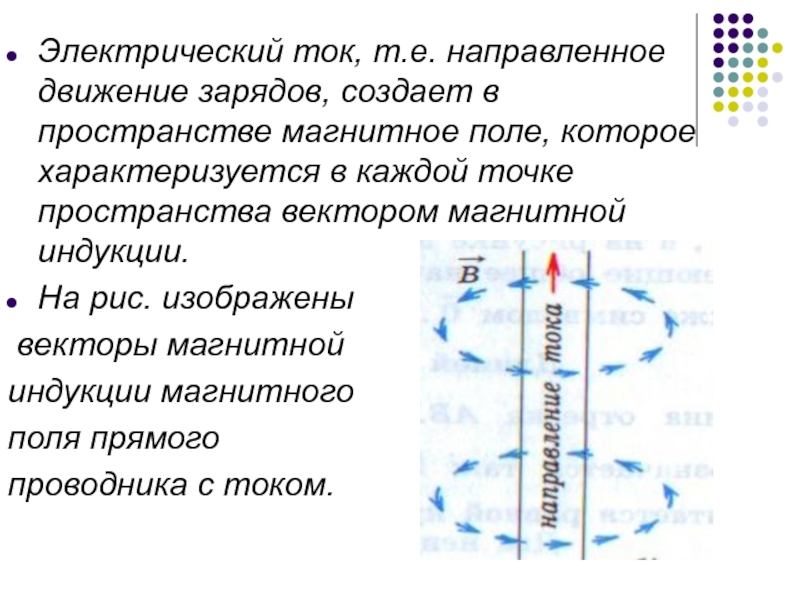
- 4. Электрический ток, т.е. направленное движение зарядов, создает
- 5. ВЕКТОР – отрезок, для которого указано, какой
- 6. ДЛИНА ВЕКТОРАДЛИНОЙ НЕНУЛЕВОГО ВЕКТОРА НАЗЫВАЕТСЯ ДЛИНА ОТРЕЗКА.ОБОЗНАЧАЕТСЯ:
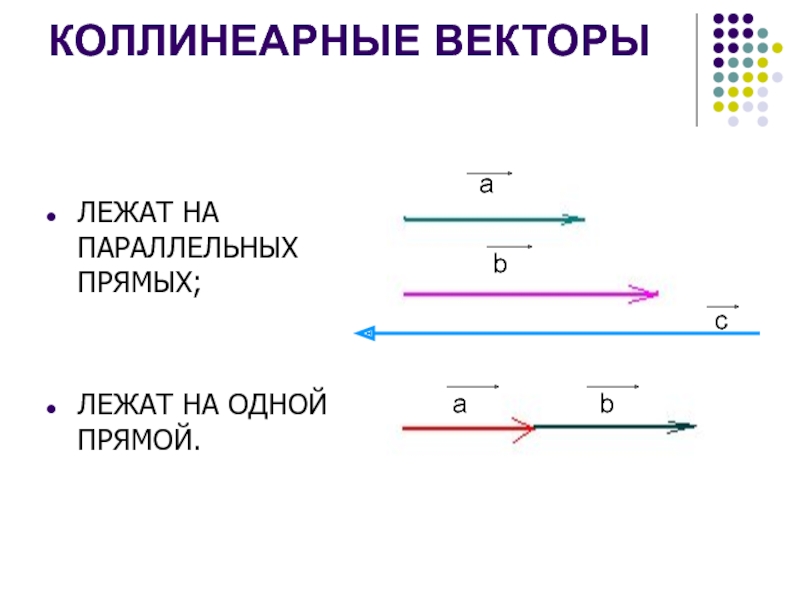
- 7. КОЛЛИНЕАРНЫЕ ВЕКТОРЫЛЕЖАТ НА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ;ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ.ababс
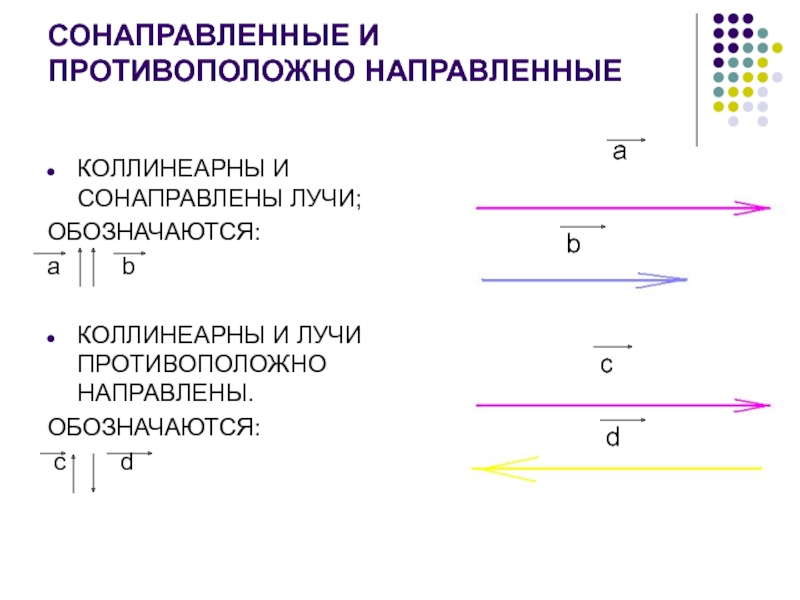
- 8. СОНАПРАВЛЕННЫЕ И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕКОЛЛИНЕАРНЫ И СОНАПРАВЛЕНЫ ЛУЧИ;ОБОЗНАЧАЮТСЯ:a
- 9. РАВНЫЕ ВЕКТОРАВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИСОНАПРАВЛЕНЫ И
- 10. Постройте 1) вектор с началом в точке
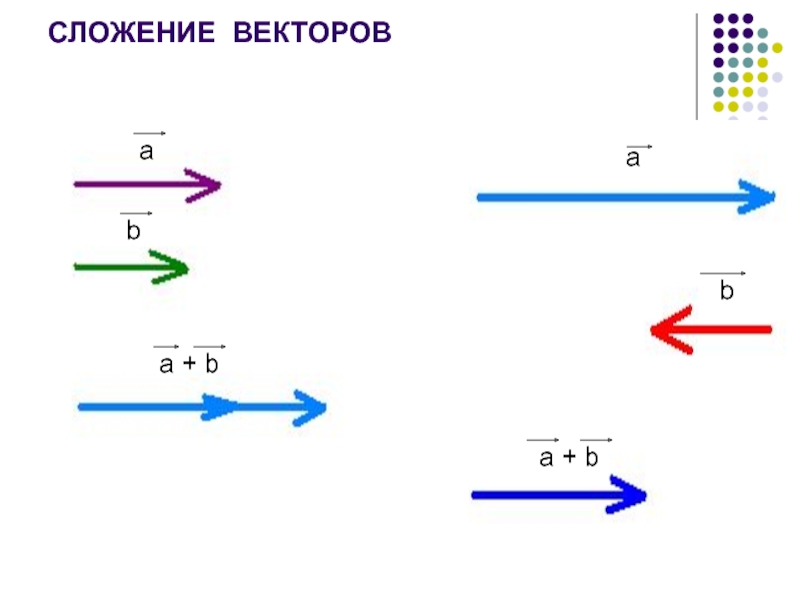
- 11. СЛОЖЕНИЕ ВЕКТОРОВaba + baba + b
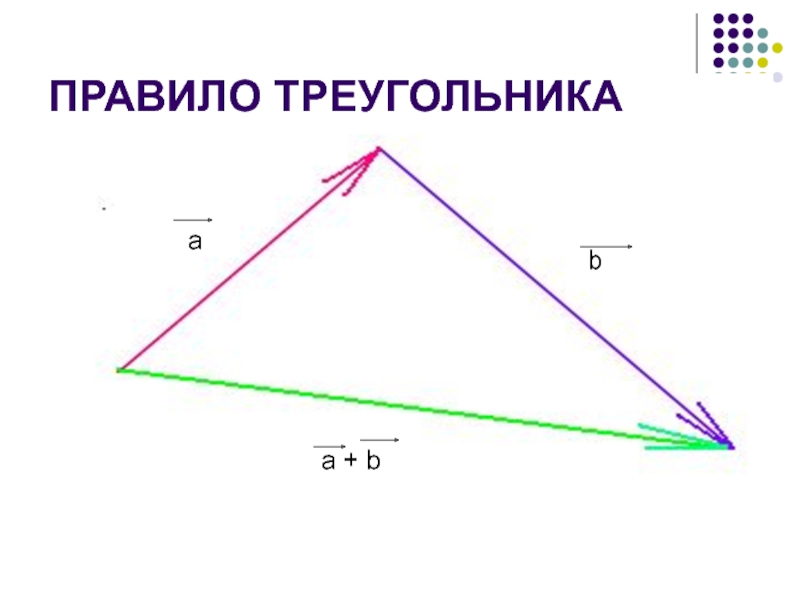
- 12. ПРАВИЛО ТРЕУГОЛЬНИКАaba + b
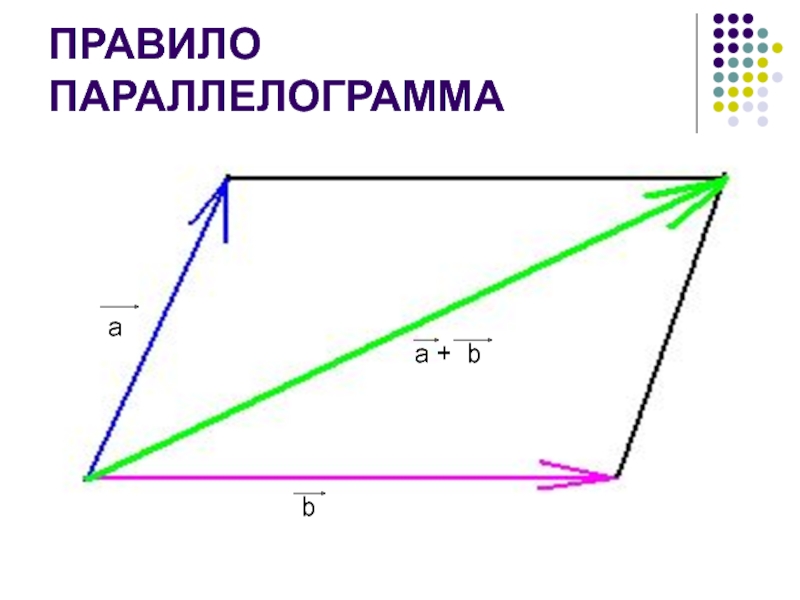
- 13. ПРАВИЛО ПАРАЛЛЕЛОГРАММАaba + b
- 14. Правило многоугольникаОСВАabca + b + c
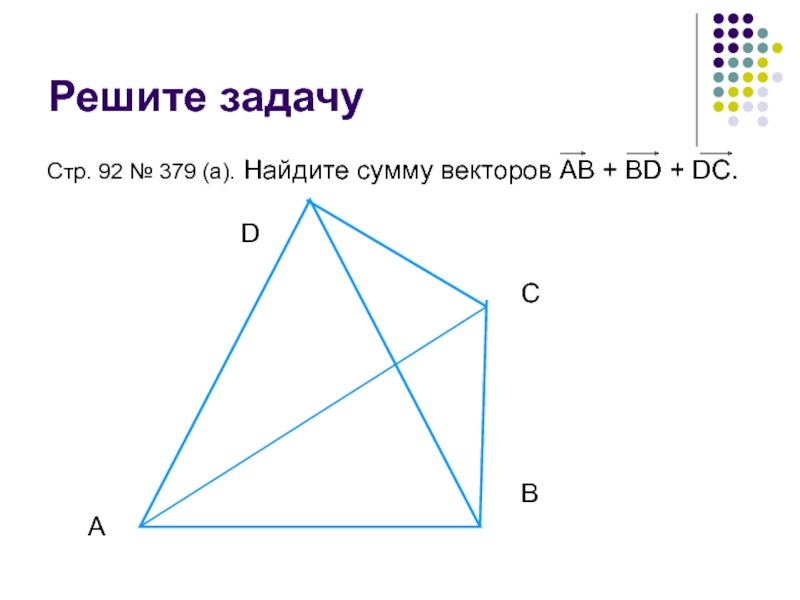
- 15. Решите задачуСтр. 92 № 379 (а). Найдите сумму векторов АВ + ВD + DC.ABCD
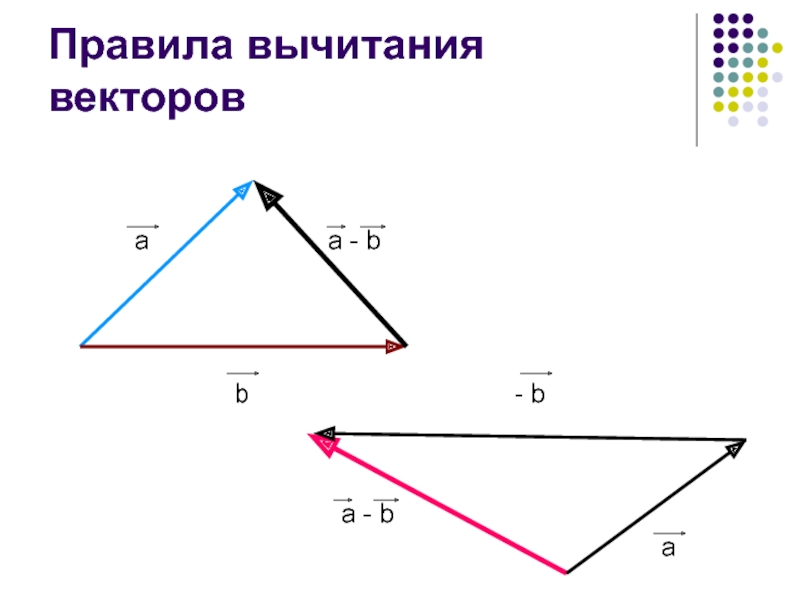
- 16. Правила вычитания векторовaba - b- baa - b
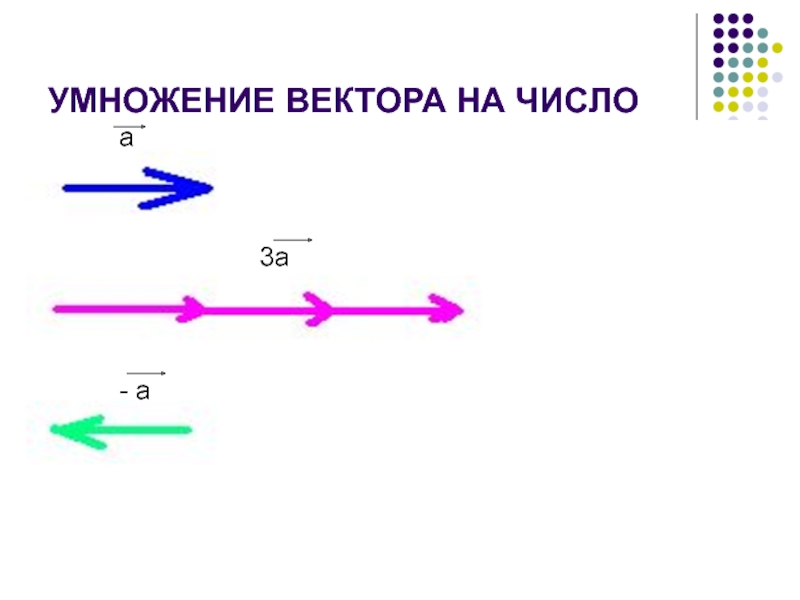
- 17. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛОa3a- a
- 18. ЗАКОНЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ НА ЧИСЛО.а +
- 19. Решите задачуСтр. 84 № 347(а).Упростите: 2 (m
- 20. Итоги урока да – 1, нет –
- 21. Домашнее заданиеСтр. 92 № 379 (б);Стр. 84
- 22. Слайд 22
- 23. Скачать презентанцию
Понятие вектора Многие физические величины, например сила, перемещение, скорость, являются векторными величинами. А также при изучении электрических и магнитных явлений используются векторные величины.
Слайды и текст этой презентации
Слайд 1Векторы в пространстве
Понятие вектора в пространстве.
Сложение и вычитание векторов.
Умножение вектора
на число.
Слайд 2Понятие вектора
Многие физические величины, например сила, перемещение, скорость,
являются векторными величинами.
А также при изучении электрических и
магнитных явлений используются векторные величины.
Слайд 3Электрическое поле, создаваемое
в пространстве зарядами, характеризуется в каждой точке
пространства вектором
напряженности электрического поля.
На рис. изображены
векторы напряженности
электрического
поля положительного
точечного заряда.
Слайд 4Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное
поле, которое характеризуется в каждой точке пространства вектором магнитной индукции.
На
рис. изображенывекторы магнитной
индукции магнитного
поля прямого
проводника с током.
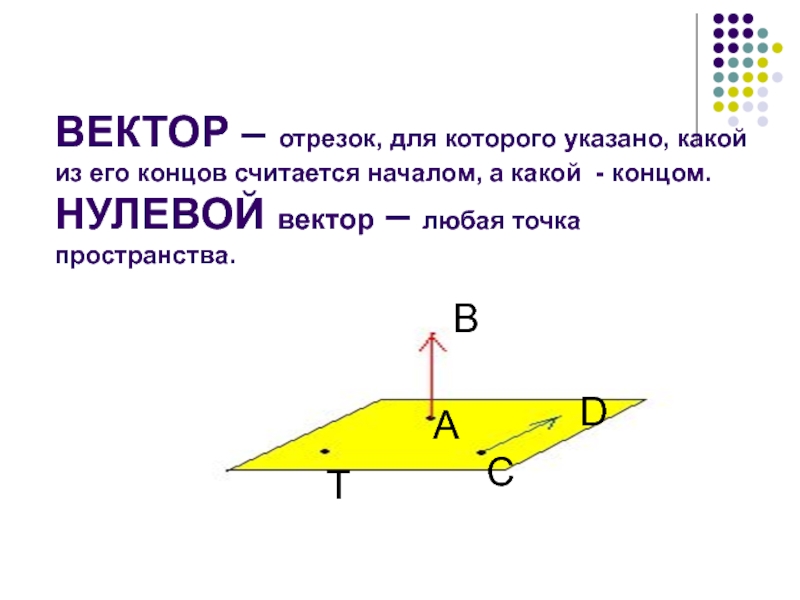
Слайд 5ВЕКТОР – отрезок, для которого указано, какой из его концов
считается началом, а какой - концом. НУЛЕВОЙ вектор – любая точка
пространства.T
A
B
C
D
Слайд 6ДЛИНА ВЕКТОРА
ДЛИНОЙ НЕНУЛЕВОГО ВЕКТОРА НАЗЫВАЕТСЯ ДЛИНА ОТРЕЗКА.
ОБОЗНАЧАЕТСЯ: | a |
или | АВ |
ДЛИНА НУЛЕВОГО ВЕКТОРА СЧИТАЕТСЯ РАВНОЙ НУЛЮ.
ОБОЗНАЧАЕТСЯ:| 0
| =0
Слайд 8СОНАПРАВЛЕННЫЕ И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ
КОЛЛИНЕАРНЫ И СОНАПРАВЛЕНЫ ЛУЧИ;
ОБОЗНАЧАЮТСЯ:
a
b
КОЛЛИНЕАРНЫ И ЛУЧИ ПРОТИВОПОЛОЖНО НАПРАВЛЕНЫ.
ОБОЗНАЧАЮТСЯ:
c
da
b
c
d
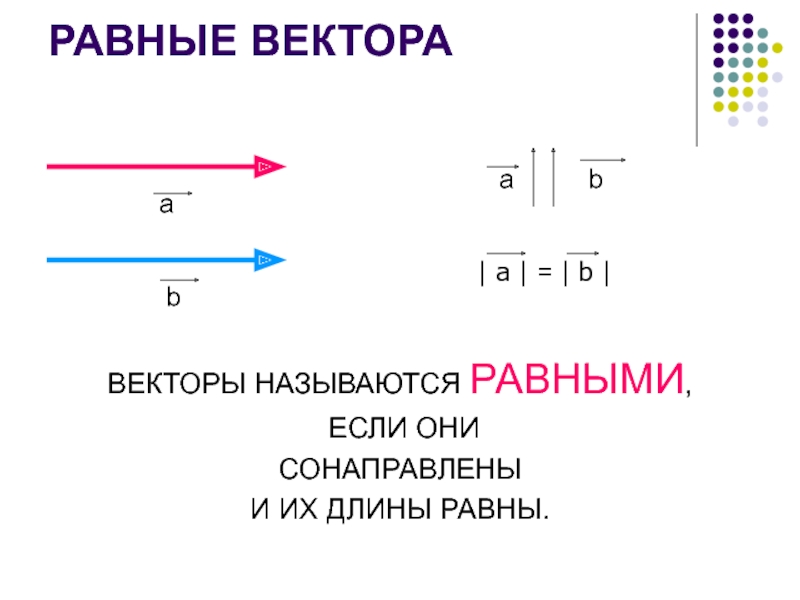
Слайд 9РАВНЫЕ ВЕКТОРА
ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ,
ЕСЛИ ОНИ
СОНАПРАВЛЕНЫ
И ИХ ДЛИНЫ
РАВНЫ.
a
b
| a | = | b |
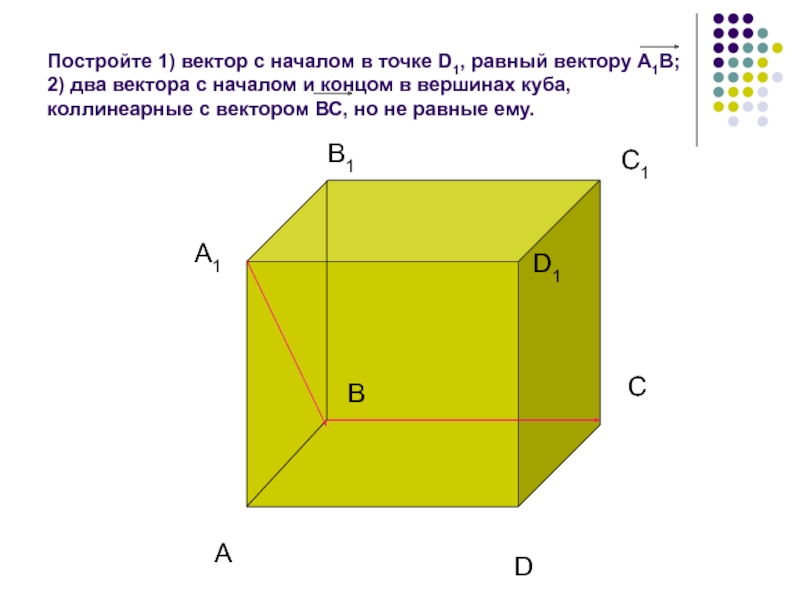
a b
Слайд 10Постройте 1) вектор с началом в точке D1, равный вектору
А1В; 2) два вектора с началом и концом в вершинах куба,
коллинеарные с вектором ВС, но не равные ему.А
D
B
C
A1
B1
C1
D1
Слайд 18ЗАКОНЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ НА ЧИСЛО.
а + b = b
+ а (переместительный)
(а + b) + с = а +
(b + с) (сочетательный)(k n) a = k (n a) (сочетательный)
k (a + b) = ka + kb (распределительный)
(k + n) a = ka + na (распределительный)
Слайд 20Итоги урока
да – 1, нет – 0.
Справедливо ли
утверждение:
Любые два противоположно направленных вектора коллинеарны;
(да)
Любые два коллинеарных вектора сонаправлены;
(нет)
Любые два равных вектора коллинеарны;
(да)
Любые два сонаправленных вектора равны.
(нет)
Может ли длина суммы двух векторов быть меньше длины каждого из слагаемых?
(да)
Ответ: 10101
Слайд 21Домашнее задание
Стр. 92 № 379 (б);
Стр. 84 № 347 (б).
Учить
законы сложения и вычитания векторов, умножения вектора на число.
