Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координатный метод при решении задач Стереометрии 11 класс
Содержание
- 1. Координатный метод при решении задач Стереометрии 11 класс
- 2. Типы задач:расстояние от точки до плоскости;расстояние от
- 3. Суть метода координат:введение ( привязка к исследуемым
- 4. Алгоритм применения КВМ Выбрать в пространстве систему
- 5. Основные формулыЕсли М1(х1;у1;z1),М2(х2;у2;z2), то
- 6. Основные формулыЕсли а (а1;а2;а3), в (b1; b2;
- 7. Основные формулыУсловие коллинеарности векторов а (а1;а2;а3) и
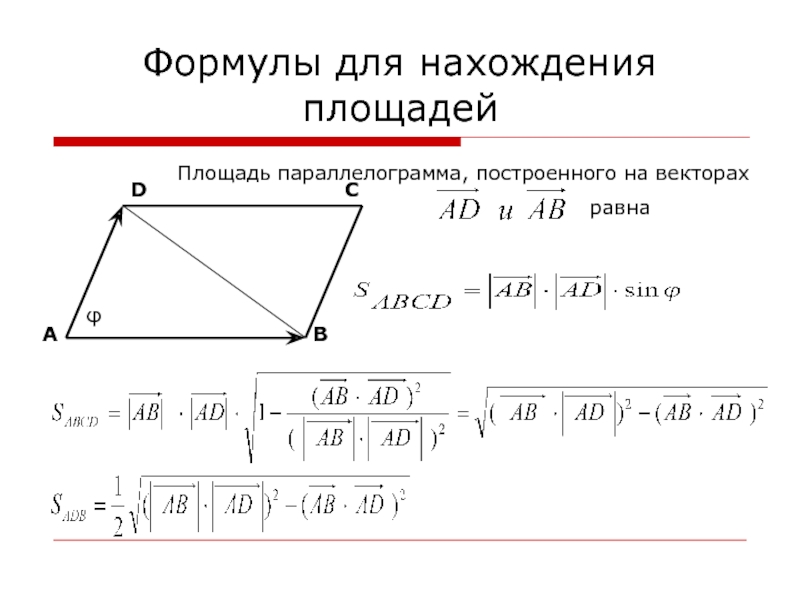
- 8. Формулы для нахождения площадейПлощадь параллелограмма, построенного на
- 9. Уравнения прямой и плоскостиКаноническое уравнение прямой:
- 10. Формулы нахождения расстояния от точки до плоскостиЕсли
- 11. Задача1. Найти угол между двумя прямыми
- 12. Задача 2. Найти угол между прямой d
- 13. ЗАДАЧАРебро куба ABCDA1B1C1D1 равно 4. Точка K
- 14. Решение:MHKABCDD1A1B1C1xyz(3;0;4)(1;0;0)(4;4;2)(0;4;4)1. Пусть α искомый угол.
- 15. ЗАДАЧА (ЕГЭ 2006)В правильной четырехугольной пирамиде SABCD
- 16. 1. Введем систему координат, взяв за единичный
- 17. ЗАДАЧАОснованием прямой призмы ABCA1B1C1 является прямоугольный треугольник
- 18. Решение:MFNДано: ABCA1B1C1 – прямая призма
- 19. ЗАДАЧА (ЕГЭ 2007)В треугольной пирамиде ABCD все
- 20. Решение:Дано: DABC – тетраэдр
- 21. Достоинства и недостатки метода координат:Этот метод
- 22. Используемая литература.Александро А.Д., Вернер А.Л., Рыжик В.И.
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Муниципальное автономное образовательное учреждение
г. Владимира
«Средняя образовательная школа № 14»
Координатный
метод при решении задач
Слайд 2Типы задач:
расстояние от точки до плоскости;
расстояние от точки до прямой;
угол
между прямой и плоскостью;
угол между скрещивающимися прямыми;
угол между плоскостями;
комбинированные задачи,
в которых известно данное одного типа, а найти нужно данное другого или других типов.Слайд 3Суть метода координат:
введение ( привязка к исследуемым фигурам) декартовой системы
координат, а затем – вычисление длин образующихся векторов или углов
между ними.Слайд 4Алгоритм применения КВМ
Выбрать в пространстве систему координат из соображений
удобства выражения координат и наглядности изображения.
Найти координаты необходимых точек.
Решить задачу,
используя основные задачи метода координат.Перейти от аналитических соотношений к геометрическим.
Слайд 5Основные формулы
Если М1(х1;у1;z1),М2(х2;у2;z2), то
М1М2{х2-х1;у2-у1;z2- z1};
(1)|М1М2|=√ (х2-х1)2+(у2-у1)2+(z2- z1)2 (2)
Если М(х;у;z) - середина отрезка М1М2, то
Х= (3)
Слайд 6Основные формулы
Если а (а1;а2;а3), в (b1; b2; b3), то
а ·в =а 1·
b 1+а 2· b 2+а 3· b 3; (4)а ·в =|а|·|в|· (5)
= = (6)
(7)
Слайд 7Основные формулы
Условие коллинеарности векторов
а (а1;а2;а3) и в (b1;
b2; b3):
(8)Уравнение сферы с центром в т.С(х0;у0;z0) и радиусом r имеет вид:
(x – x0)2 + (y – y0)2 + (z – z0)2 = r2; (9)
Слайд 9Уравнения прямой и плоскости
Каноническое уравнение прямой:
,
где М(х0,у0,z0) , авектор является направляющим
Уравнение прямой, заданной 2-мя точками: М1(х1;у1;z1) и
М2(х2;у2;z2) имеет вид:
Уравнение плоскости, заданной точкой М(х0,у0,z0) и вектором нормали (любым ненулевым вектором, перпендикулярным плоскости):
Ах+Ву+Сz+D=0, где D=-(Ax0+Bу0+Сz0)
Слайд 10Формулы нахождения расстояния от точки до плоскости
Если точка М(х0,у0,z0), а
плоскость α задана уравнением Ах+Ву+Сz+D=0, то расстояние от точки М
до плоскости α вычисляется по формуле:Слайд 11 Задача1. Найти угол между двумя прямыми d1 и d2 (пересекающимися
или скрещивающимися), если направляющие векторы этих прямых известны.
Пусть а (a1;а2;а3),
b (b1; b2; b3) – направляющие векторы этих прямых, а φ – искомый угол.
Обозначим через .Тогда φ= , если ≤ 900 ,
либо φ= 1800 - , если > 900. Поэтому либо cosφ = cos , либо cosφ =-cos .
В любом случае , а т.к. φ ≤ 900, то cos φ ≥0, и, следовательно, cosφ= .
Получаем:
=
cosφ=
=
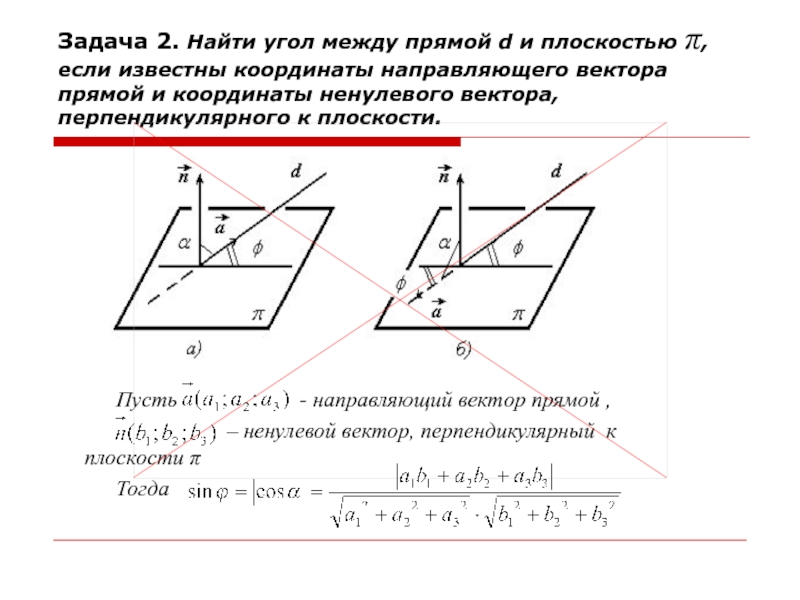
Слайд 12Задача 2. Найти угол между прямой d и плоскостью π,
если известны координаты направляющего вектора прямой и координаты ненулевого вектора,
перпендикулярного к плоскости.Пусть - направляющий вектор прямой ,
– ненулевой вектор, перпендикулярный к плоскости π
Тогда
Слайд 13ЗАДАЧА
Ребро куба ABCDA1B1C1D1 равно 4. Точка K середина ребра DD1.
Точки M и H лежат на ребрах A1B1 и AB
соответственно, причем A1M:MB1=1:3, AH:HB=3:1.Найти градусную меру угла между прямыми MH и KC1.
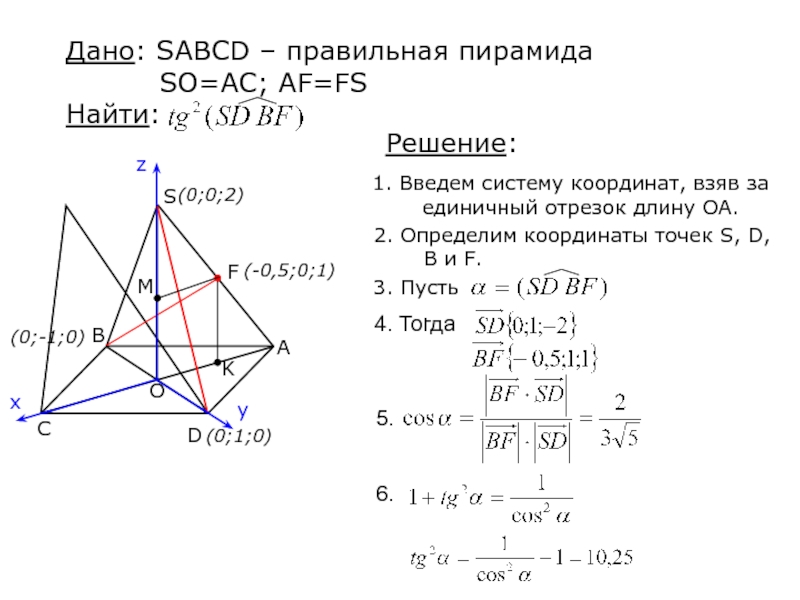
Слайд 15ЗАДАЧА (ЕГЭ 2006)
В правильной четырехугольной пирамиде SABCD с вершиной S
высота равна диагонали основания. Точка F лежит на середине ребра
SA.Найдите квадрат тангенса угла между прямыми SD и BF.
Слайд 161. Введем систему координат, взяв за единичный отрезок длину OA.
2.
Определим координаты точек S, D, B и F.
Дано: SABСD –
правильная пирамида
SO=AC; AF=FS
Найти: F
(0;-1;0)
(0;1;0)
(0;0;2)
(-0,5;0;1)
Решение:
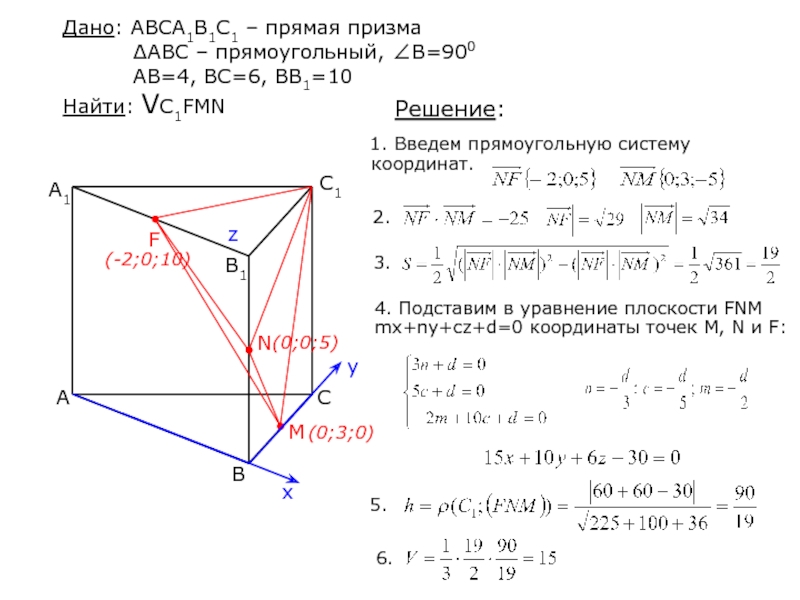
Слайд 17ЗАДАЧА
Основанием прямой призмы ABCA1B1C1 является прямоугольный треугольник с катетами AB=4
и BC=6. Высота призмы равна 10.
Найдите объем пирамиды с вершинами
в точке C1 и серединах ребер BC, BB1 и A1B1.Слайд 18Решение:
M
F
N
Дано: ABCA1B1C1 – прямая призма
∆ABC
– прямоугольный, ∠B=900 AB=4, BC=6, BB1=10 Найти:
VC1FMN(0;3;0)
(0;0;5)
(-2;0;10)
1. Введем прямоугольную систему координат.
4. Подставим в уравнение плоскости FNM mx+ny+cz+d=0 координаты точек M, N и F:
Слайд 19ЗАДАЧА (ЕГЭ 2007)
В треугольной пирамиде ABCD все ребра имеют одинаковую
длину.
Точка M – середина ребра AD, точка O –
центр треугольника ABC, точка N - середина ребра AB и точка K – середина ребра CD. Найдите угол между прямыми MO и KN.
Слайд 20Решение:
Дано: DABC – тетраэдр
M –
середина AD, O – центр ∆ABC, N – середина AB,
K- середина CD Найти: угол между MO и KN.1. Примем длину ребра тетраэдра за единицу и выберем в качестве базиса векторы
2. Составим таблицу умножения для этого базиса (Таблица 1).
M
O
K
N
Таблица 1
6. Пользуясь таблицей 1, получим:
Слайд 21Достоинства и недостатки
метода координат:
Этот метод не требуют рассмотрения сложных
геометрических конфигураций.
Все те соотношения, которые при решении традиционным методом
даются с большим трудом (через привлечение большого количества вспомогательных теорем), здесь получаются как бы сами собой, в ходе вычислений. Сводит геометрическую задачу к алгебраической, решить которую обычно легче, чем исходную геометрическую
Недостаток – это большой объем вычислений.
Слайд 22Используемая литература.
Александро А.Д., Вернер А.Л., Рыжик В.И. Стереометрия. Геометрия в
пространстве ALFA,1998
Беккер Б.М., Некрасов В.Б. Применение векторов к решению задач.
С-П:, 1997 Гельфанд И.М. Метод координат.- М.: Наука, 1973
Гущин Д.Д. Материалы вступительных экзаменов по математике. Для поступающих в СПбГУ,2003
Журналы «Математика в школе», «Квант».
Метод координат. Методическая разработка для уч-ся заочного отделения МГУ им. М.В.Ломоносова М.,2008
Прасолов В.В.,Шарыгин И.Ф. Задачи по стереометрии Москва, «Наука»,1989г.
Севрюков П.Ф.,Смоляков А.Н. Векторы и координаты в решении задач школьного курса стереометрии