Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Третий признак равенства треугольников
Содержание
- 1. Третий признак равенства треугольников
- 2. Прежде необходимо вспомнитьКаков бы ни был треугольник,
- 3. Теорема 3.6 (признак равенства треугольников по трем
- 4. Признак равенства треугольников по трем сторонам
- 5. Признак равенства треугольников по трем сторонам
- 6. Признак равенства треугольников по трем сторонам
- 7. Признак равенства треугольников по трем сторонам
- 8. Признак равенства треугольников по трем сторонам
- 9. Признак равенства треугольников по трем сторонам
- 10. Признак равенства треугольников по трем сторонам
- 11. Признак равенства треугольников по трем сторонам
- 12. Признак равенства треугольников по трем сторонам
- 13. Признак равенства треугольников по трем сторонам
- 14. Теорема 3.6 (признак равенства треугольников по трем
- 15. Скачать презентанцию
Прежде необходимо вспомнитьКаков бы ни был треугольник, существует равный ему треугольник в заданной расположении относительно данной полупрямой. (аксиома IV3)В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. (теорема 3.5)Через
Слайды и текст этой презентации
Слайд 1
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Создатель презентации учитель математики Старогутнянской школы
Авдащенко
Василий Александрович
Слайд 2Прежде необходимо вспомнить
Каков бы ни был треугольник, существует равный ему
треугольник в заданной расположении относительно данной полупрямой. (аксиома IV3)
В равнобедренном
треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. (теорема 3.5)Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну. (теорема 2.3)
Доказательство от противного.
Слайд 3Теорема 3.6
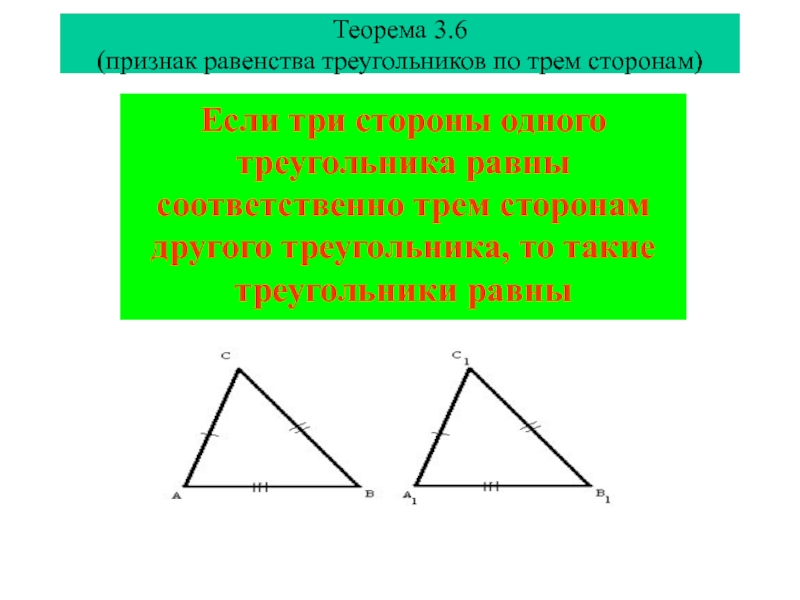
(признак равенства треугольников по трем сторонам)
Если три стороны одного
треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники
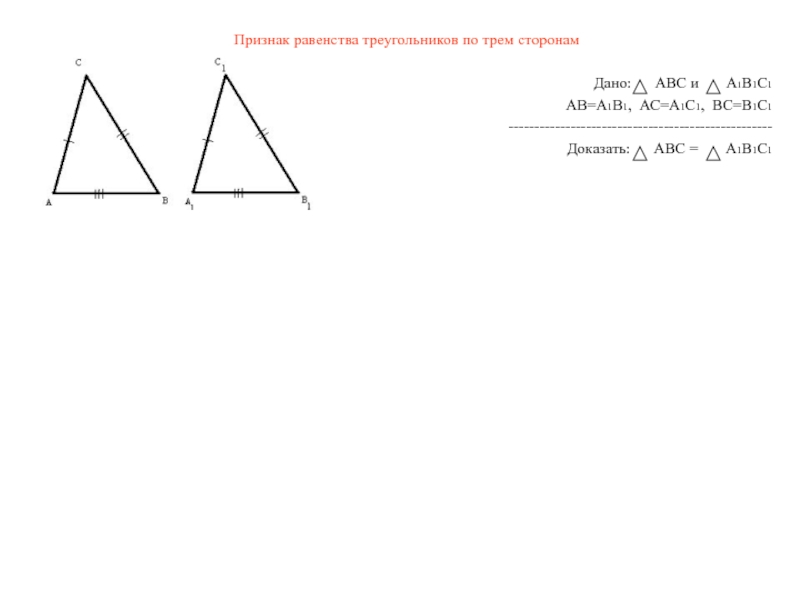
равныСлайд 4Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
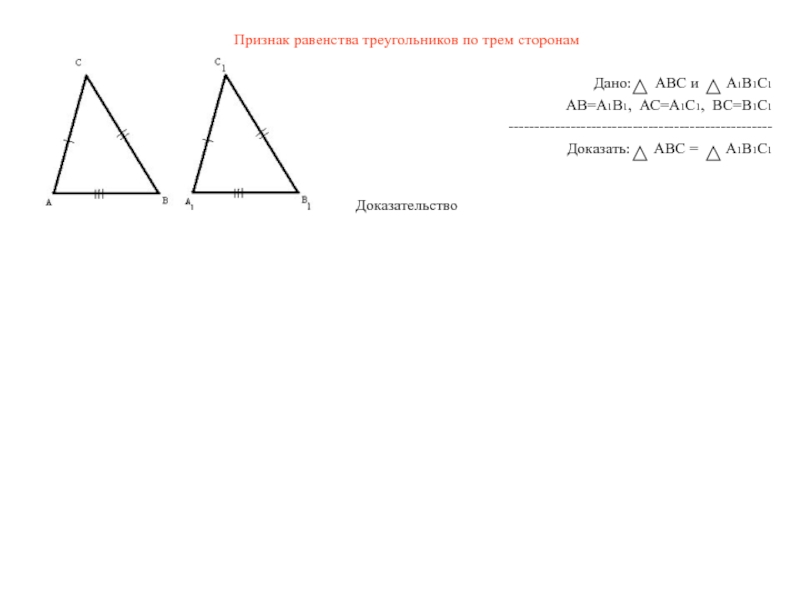
Слайд 5Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
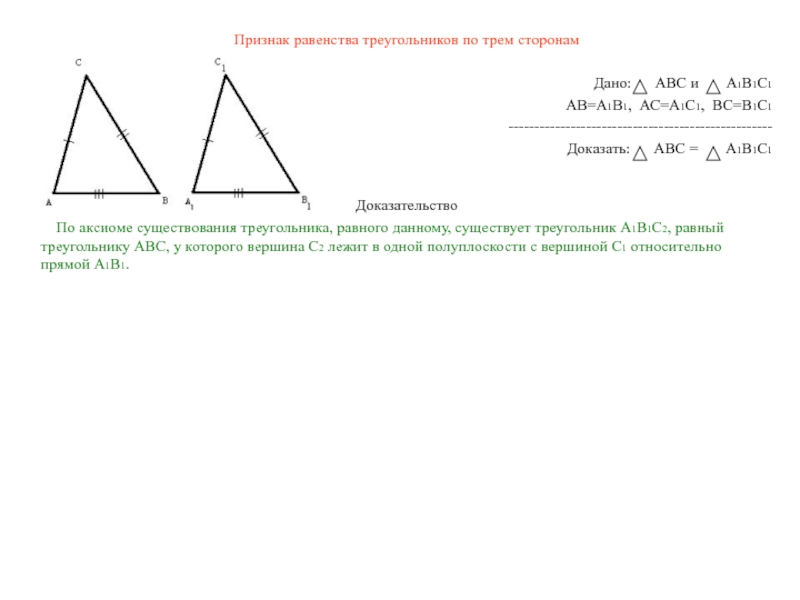
Слайд 6Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
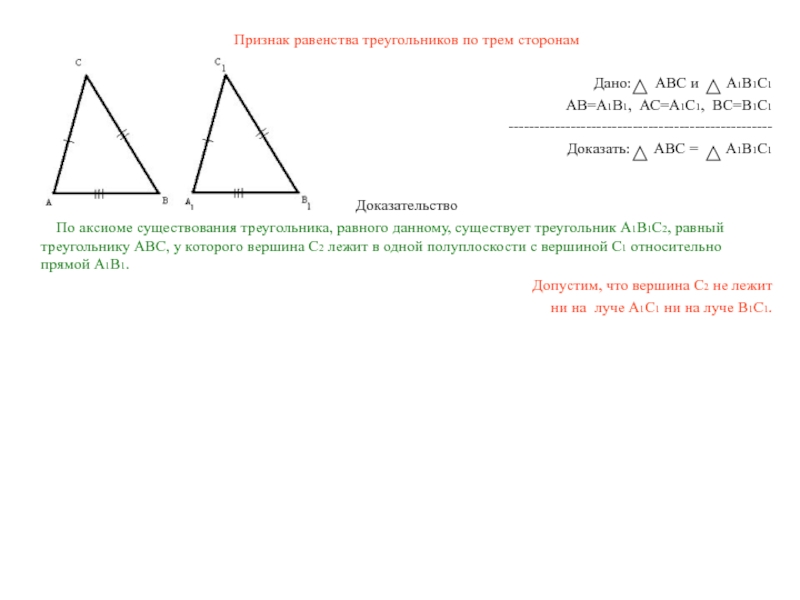
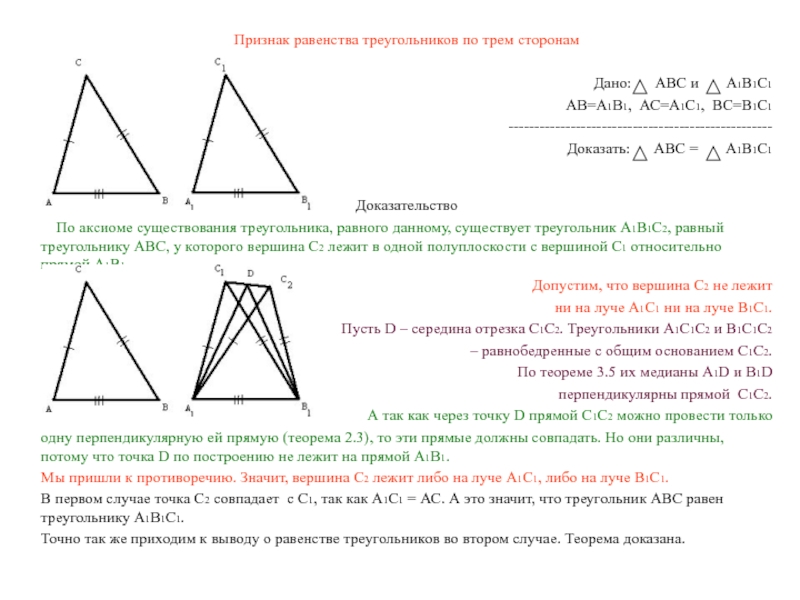
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Слайд 7Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Слайд 8Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Слайд 9Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
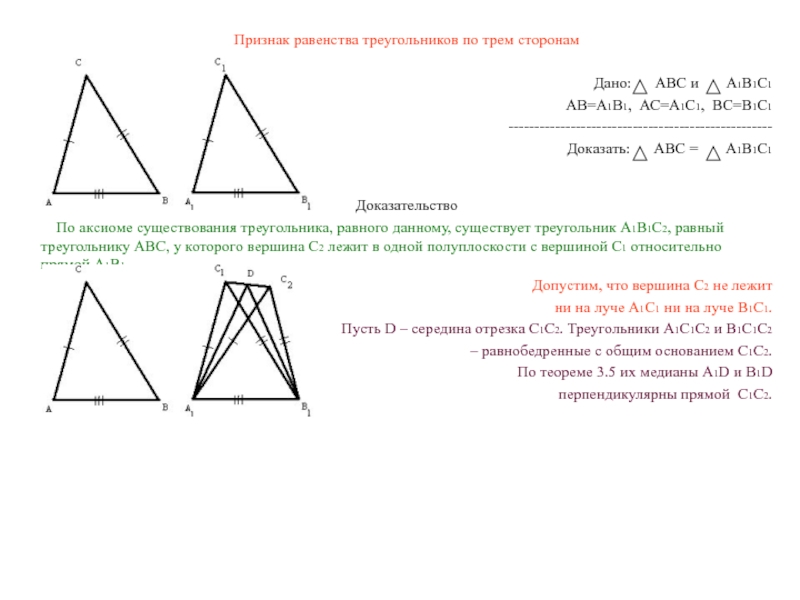
Пусть D – середина отрезка С1С2. Треугольники А1С1С2 и В1С1С2
– равнобедренные с общим основанием С1С2.
По теореме 3.5 их медианы А1D и В1D
перпендикулярны прямой C1C2.
Слайд 10Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Пусть D – середина отрезка С1С2. Треугольники А1С1С2 и В1С1С2
– равнобедренные с общим основанием С1С2.
По теореме 3.5 их медианы А1D и В1D
перпендикулярны прямой C1C2.
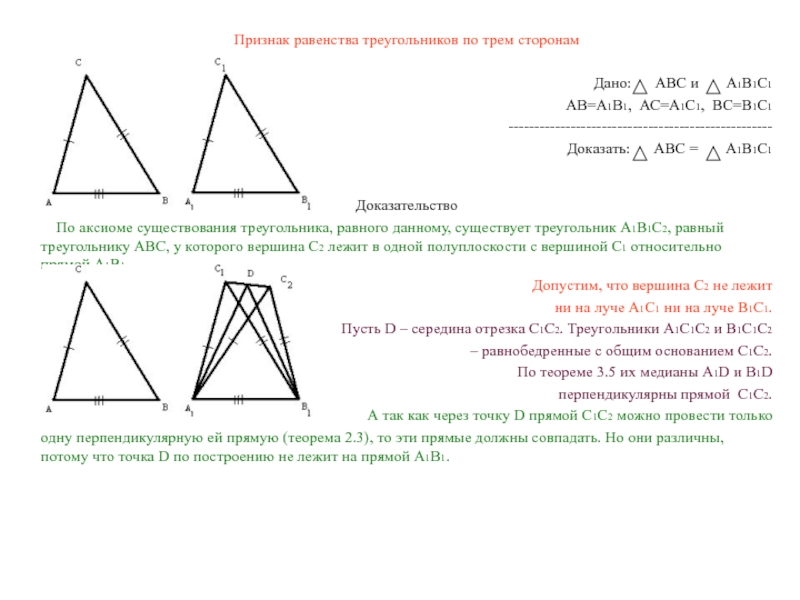
А так как через точку D прямой С1С2 можно провести только
одну перпендикулярную ей прямую (теорема 2.3), то эти прямые должны совпадать. Но они различны, потому что точка D по построению не лежит на прямой А1В1.
Слайд 11Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Пусть D – середина отрезка С1С2. Треугольники А1С1С2 и В1С1С2
– равнобедренные с общим основанием С1С2.
По теореме 3.5 их медианы А1D и В1D
перпендикулярны прямой C1C2.
А так как через точку D прямой С1С2 можно провести только
одну перпендикулярную ей прямую (теорема 2.3), то эти прямые должны совпадать. Но они различны, потому что точка D по построению не лежит на прямой А1В1.
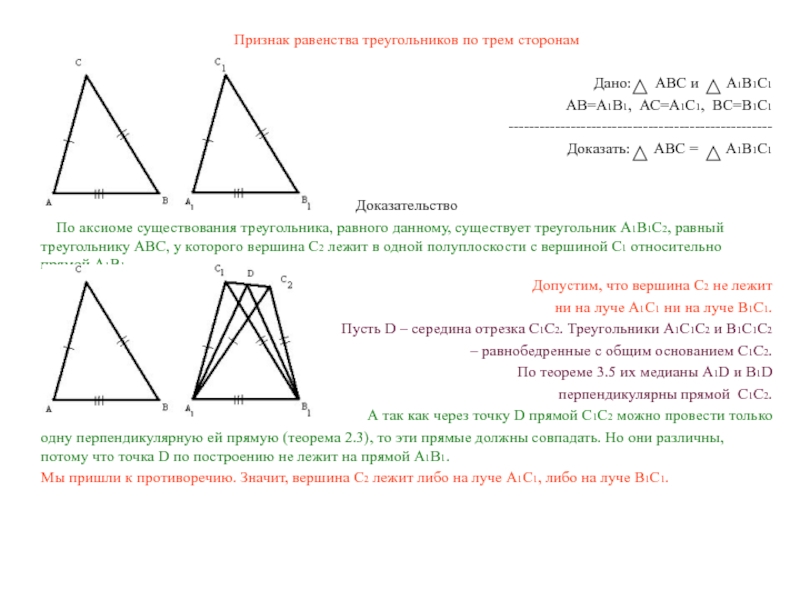
Мы пришли к противоречию. Значит, вершина С2 лежит либо на луче А1С1, либо на луче В1С1.
Слайд 12Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Пусть D – середина отрезка С1С2. Треугольники А1С1С2 и В1С1С2
– равнобедренные с общим основанием С1С2.
По теореме 3.5 их медианы А1D и В1D
перпендикулярны прямой C1C2.
А так как через точку D прямой С1С2 можно провести только
одну перпендикулярную ей прямую (теорема 2.3), то эти прямые должны совпадать. Но они различны, потому что точка D по построению не лежит на прямой А1В1.
Мы пришли к противоречию. Значит, вершина С2 лежит либо на луче А1С1, либо на луче В1С1.
В первом случае точка С2 совпадает с С1, так как А1С1 = АС. А это значит, что треугольник АВС равен треугольнику А1В1С1.
Слайд 13Признак равенства треугольников по трем сторонам
Дано: АВС и А1В1С1
АВ=А1В1, АС=А1С1, ВС=В1С1
---------------------------------------------------
Доказать: АВС = А1В1С1
Доказательство
По аксиоме существования треугольника, равного данному, существует треугольник А1В1С2, равный треугольнику АВС, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой А1В1.
Допустим, что вершина С2 не лежит
ни на луче А1С1 ни на луче В1С1.
Пусть D – середина отрезка С1С2. Треугольники А1С1С2 и В1С1С2
– равнобедренные с общим основанием С1С2.
По теореме 3.5 их медианы А1D и В1D
перпендикулярны прямой C1C2.
А так как через точку D прямой С1С2 можно провести только
одну перпендикулярную ей прямую (теорема 2.3), то эти прямые должны совпадать. Но они различны, потому что точка D по построению не лежит на прямой А1В1.
Мы пришли к противоречию. Значит, вершина С2 лежит либо на луче А1С1, либо на луче В1С1.
В первом случае точка С2 совпадает с С1, так как А1С1 = АС. А это значит, что треугольник АВС равен треугольнику А1В1С1.
Точно так же приходим к выводу о равенстве треугольников во втором случае. Теорема доказана.