Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач на смеси, растворы и сплавы
Содержание
- 1. Решение задач на смеси, растворы и сплавы
- 2. Задача № 1
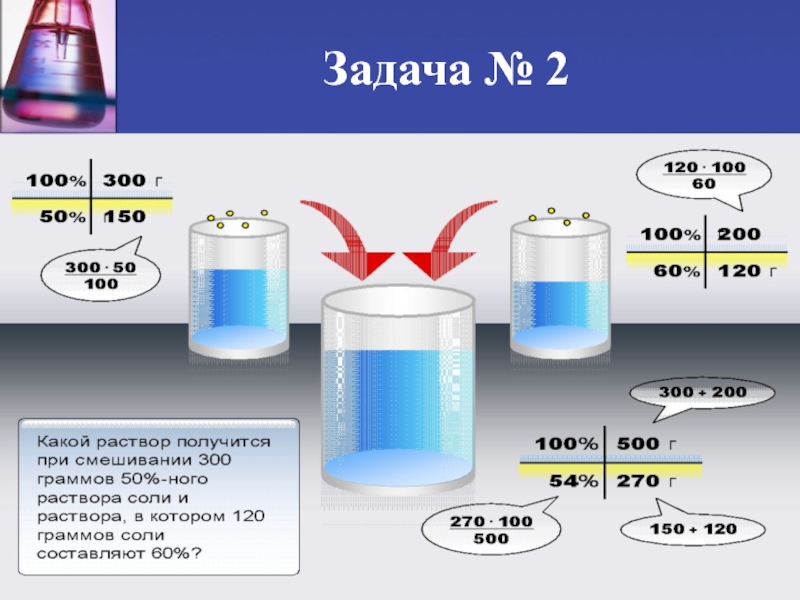
- 3. Задача № 2
- 4. Имеются сплавы золота и серебра. В одном
- 5. Имеются два сплава меди со свинцом. Один
- 6. Смешали 30%-й раствор соляной кислоты с 10%-ым
- 7. Имеется лом стали двух сортов с содержанием
- 8. Имеется два кислотных раствора: один 20%, другой
- 9. Имеется руда из двух пластов с содержанием
- 10. Старинный способ решения задач на смешивание двух
- 11. Способ Л.Ф.Магницкого для трех веществНекто имеет чай
- 12. Сплавили два слитка серебра: 75 г
- 13. «Правило креста» При решении задач на смешивание
- 14. От двух кусков сплава с массами 3
- 15. Латунь – сплав меди и цинка. Кусок
- 16. В бидон налили 4л молока трехпроцентной жирности
- 17. ЕГЭ - 2009 задачи на
- 18. «Только из союза двоих, работающих вместе и
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Имеются сплавы золота и серебра. В одном эти металлы находятся
в отношении 2: 3, а в другом в отношении 3:
7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?
По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
*х + * у = * 1
Аналогично массу серебра и получаем уравнение
* х + * у = * 1
Записываем одну из систем:
х + у = 1
х + у =
х + у = 1
х + у =
Решая ее, получаем х = 0,125 и у = 0,875
Ответ: 125 г и 875 г.
Слайд 5Имеются два сплава меди со свинцом. Один сплав содержит 15%
меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы
получилось 200г сплава, содержащего 30% меди?1. Изобразим сплавы в виде прямоугольников
М С М С
+ =
х(г) (200 –х) (г) 200 (г)
0,15х + 0,65(200 – х) = 0,3 *200 х = 140
2. Обозначим
М С М С
+ =
х(г) у(г) 200(г)
х + у = 200
0,15х + 0,65у =0,3 *200
х = 140 и у = 60
Ответ: 140г меди и 60г свинца
15%
65%
30%
15%
65%
30%
Слайд 6Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили
600 г 15%-го раствора. Сколько граммов каждого раствора надо было
взять?Решение 1: аналитическая модель. Обозначим x массу первого
раствора, тогда масса второго (600 - x). Составим уравнение:
30x + 10* (600 - x) = 600 *15 x = 150
Решение 2: с использованием графика.
Приравнивание площадей равновеликих прямоугольников:
15x = 5 (600- x)
x =150
Ответ: 150г 30% и 450г 10% раствора
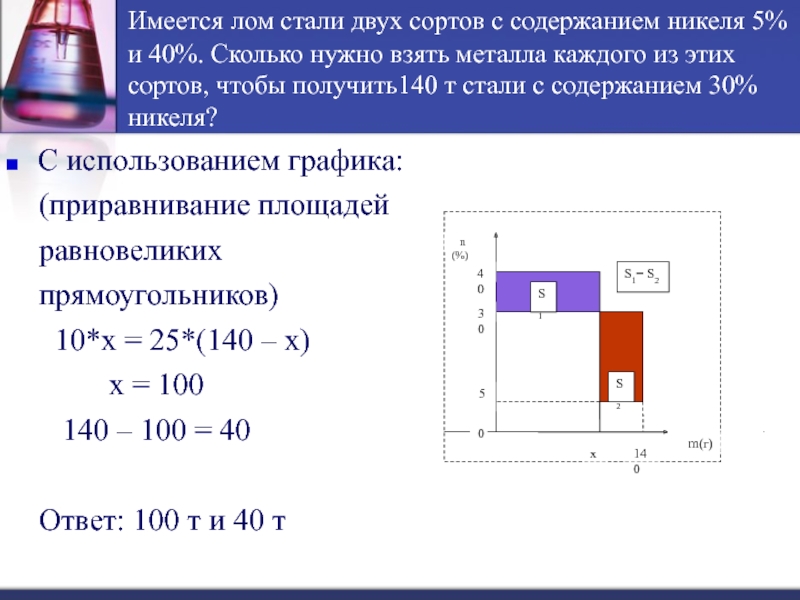
Слайд 7Имеется лом стали двух сортов с содержанием никеля 5% и
40%. Сколько нужно взять металла каждого из этих сортов, чтобы
получить140 т стали с содержанием 30% никеля?С использованием графика:
(приравнивание площадей
равновеликих
прямоугольников)
10*х = 25*(140 – х)
х = 100
140 – 100 = 40
Ответ: 100 т и 40 т
Слайд 8Имеется два кислотных раствора: один 20%, другой 30%. Взяли 0,5
л первого и 1,5 л второго раствора и образовали новый
раствор. Какова концентрация кислоты в новом растворе?Так как первый раствор 20 % - й, то в нем 0,2 объема занимает «чистая» кислота. Так как объем первого раствора равен 0,5л, то в этом количестве содержится 0,2*0,5=0,1 л «чистой» кислоты.
Аналогично во втором растворе будет содержаться 0,3*1,5=0,45л «чистой» кислоты.
При смешивании растворов получим 0,5+1,5=2л кислотного раствора, в котором 0,1+0,45=0,55л «чистой» кислоты.
Отсюда следует, что концентрация кислоты в новом растворе есть отношение 0,55:2=0,275, т.е.27,5%.
Ответ: концентрация кислоты в новом растворе 27,5%
Слайд 9Имеется руда из двух пластов с содержанием меди 6% и
11%. Сколько «бедной» руды надо взять, чтобы получить при смешивании
с «богатой» 20 т руды с содержанием меди 8%?Аналитическая модель:
Переведем проценты в дроби:
6%=0,06; 11%=0,11; 8%=0,08
Пусть надо взять х т «бедной» руды,
которая будет содержать 0,06х т меди,
а «богатой» руды надо взять (20-х) т,
которая будет содержать 0,11(20 - х) т
меди.
Так как получившиеся 20 т руды
будут содержать 20*0,08 т меди, то
получим уравнение:
0,06х + 0,11(20 - х) = 20*0,08.
Решив уравнение, получим х = 12.
Ответ: 12т руды с 6% содержанием меди
Слайд 10Старинный способ решения задач на смешивание двух веществ
У некоторого человека
были на продажу масла двух сортов: одно ценою 10 гривен
за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.
10
6
1
3
7
Слайд 11Способ Л.Ф.Магницкого для трех веществ
Некто имеет чай трех сортов –цейлонский
по 5 гривен за фунт,
индийский по 8 гривен за
фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти сорта, чтобы получить чай
стоимостью 6 гривен за фунт?
Взять 6+2=8 частей чая ценой по 5 гривен и по
одной части ценой 8 гривен и 12 гривен за один фунт.
Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и
по1/10 фунта чая ценой 8 и 12 гривен за фунт, то
получим 1 фунт чая ценой
8/10*5 + 1/10*8 + 1/10*12 = 6 гривен
6
5
12
6
1
6
5
8
1
2
6
2/8
1
1/10
Слайд 12Сплавили два слитка серебра: 75 г 600-й и 150 г
864-й пробы.
Определить пробу сплава.
Пусть проба сплава равна
х.Составим диагональную схему:
Получаем:
(864 – х) : (х – 600) = 75 : 150
1728 – 2х = х – 600
х = 776.
Ответ: сплав 776-й пробы.
Слайд 13«Правило креста»
При решении задач на смешивание растворов разных
концентраций
используется «правило креста». В точке
пересечения двух прямых обозначают концентрацию
смеси. У концов этих прямых слева от точки пересечения указывают
концентрации составных частей смеси, а справа – разности
концентраций смеси и ее составных частей:
Например, для приготовления 30 г 80%-го раствора H3PO4
требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты.
Слайд 14От двух кусков сплава с массами 3 кг и 2
кг и с концентрацией меди 0,6 и 0,8 отрезали по
куску равной массы. Каждый из отрезанных кусков сплавлен с остатком другого куска, после чего концентрация меди в обоих сплавах стала одинаковой. Какова масса каждого из отрезанных кусков?Обозначим массу отрезанного куска х (кг).
Так как в обоих сплавах концентрация меди после двух операция
стала одинаковой, то массы сплавов и массы меди в этих сплавах
пропорциональны.
Первоначально массы меди в сплавах равны 0,6*3(кг) и 0,8*2(кг).
После того, как отрезали куски массой х(кг), содержание меди
стало 0,6(3-х) и 0,8(2-х), а после сплавления
0,6(3-х) + 0,8х и 0,8(2-х) +0,6х
= , х = 1,2
Ответ: 1,2 кг
1,8+0,2х
2
3
mм(кг)
mc(кг)
1,6-0,2х
Слайд 15Латунь – сплав меди и цинка. Кусок латуни содержит меди
на 11 кг больше, чем цинка. Этот кусок латуни сплавили
с 12 кг меди и получили латунь, в котором 75% меди. Сколько килограммов меди было в куске латуни первоначально?Обозначим искомую величину за х.
Тогда масса первоначального куска латуни 2х – 11, а его содержание меди составляет р = процентов.
Поскольку «медность» куска меди 100%, то по правилу квадрата получаем:
= , х = 22,5
Ответ: 22,5 кг меди было в куске латуни.
р
25
75
100
75 - р
Слайд 16В бидон налили 4л молока трехпроцентной жирности и 6л молока
шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
Обозначим искомую
величину за Х.По правилу квадрата получим:
Составим пропорцию:
= , х = 4,8
Ответ: 4,8 % - жирность молока.
3
6 - х
х
6
х - 3
Слайд 17 ЕГЭ - 2009
задачи на смеси и сплавы
1.Сплавили 2кг
сплава цинка и меди, содержащего 20%
цинка, и 6кг сплава цинка
и меди, содержащего 40% цинка. Найдите процентную концентрацию меди в
получившемся сплаве. Ответ: 65% меди.
2. Для приготовления маринада необходим
2% раствор уксуса. Сколько нужно добавить
воды в 100г 9%-го раствора уксуса, чтобы получить
раствор для маринада? Ответ: 350 г воды
Слайд 18«Только из союза двоих, работающих вместе и при помощи друг
друга, рождаются великие вещи».
Антуан Де Сент-Экзюпери«При единении и малое растет, при раздоре и
величайшее распадается». Саллюстий Гай Крисп