Логика как наука 9 класс

ИКТ
ГБОУ школа №297
Пушкинского р-на Санкт-Петербурга

Презентация по информатике и ИКТ

9

класс

наука о формах и законах рационального мышления.
Демокрит
Евклид
Декарт

древнегреческий философ Аристотель, который первым систематизировал формы и правила мышления,

обстоятельно исследовал категории «понятие» и «суждение», подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.

не интересуется содержанием мышления, она изучает только формы мышления. Логику

интересует не что мы мыслим, а как мы мыслим, поэтому она также часто называется формальной логикой.
Мышление всегда осуществляется в каких-то формах. В логике выделяют следующие формы мышления: понятие, суждение, умозаключение.

объекта, отличающий его от других объектов.
Например: «собака», «растение», «планета»,

«химический элемент», «смелость», «трудолюбие» и т. п.

совокупностью предметов, на которую оно распространяется.
Далекие друг от друга по

своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, «компьютер» и «молоко», «карандаш» и «ледник»); остальные понятия называются сравнимыми.

которые удобно представлять кругами Эйлера:
Равнозначность («тождество»), когда объемы понятий полностью

совпадают;

пересечение, когда объемы понятий частично совпадают;


подчинения, когда объем одного понятия полностью входит в объем другого и т.д.

А=В

или отрицается о предметах, их свойствах или отношениях между ними.

Высказывание может быть истинным или ложным. Высказывания не могут быть выражены вопросительными или побудительными предложениями, так как оценка истинности или ложности таких, предложений невозможна.
Например: «Солнце не является планетой»; «Некоторые вещества — это металлы»; «Все цифры — это знаки»; «2 ? 2 = 4» и т. п.

каждый, ни один.
Частное высказывание начинается (или можно начать) со слов:

некоторые, большинство и т.п.
Во всех других случаях высказывание является единичным.

Например: «Все рыбы умеют плавать»; «Некоторые медведи - бурые»; «Буква А-гласная»

Высказывания бывают общими,
частными или единичными.

нескольких исходных высказываний, называемых посылками, получают новое высказывание или вывод.

Пример умозаключения: «Все металлы электропроводны. Железо — это металл. Железо электропроводно».

можно выводить другие. При этом предполагается, что вывод зависит только

от способа связи входящих в него утверждений и их строения, а не от их конкретного содержания. Отсюда еще одно определение логики.
Логика — наука, изучающая методы установления истинности или ложности одних высказываний (утверждений) на основе истинности или ложности других высказываний.

к математической (от словесной формы записи рассуждений к записи рассуждений

с помощью символов). В ней появились математические методы исследования, конкретность законов. Основоположником математической логики считают философа-математика Г. В. Лейбница (1646-1716).

которая оперирует с двоичными переменными, принимающими только два значения –

«истина» или «ложь». Алгебру логики в честь ее создателя, английского математика Дж. Буля, назвали булевой алгеброй. При этом формальная логика не утратила своего значения, и в настоящее время используется в философии, юриспруденции, криминалистике, психологии и т. д.

иcпoльзyeтcя для решения сложных математических задач, при написании алгоритмов и

программ, разработке электронных устройств, компьютеров, автомати-ческих систем, в робототехнике и т. д.

методы установления их истинности или ложности с помощью алгебраических методов.
Истинность

или ложность высказывания определяется не алгеброй логики, а конкретными науками, практикой, наблюдениями.
Для алгебры логики важен не смысл высказывания, важна лишь его истинность или ложность.

слова и словосочетания «и», «или», «не», «либо..., либо», «тогда и

только тогда» и др. Такие слова и словосочетания называются логическими связками или кванторами.

являющиеся составными, называются простыми или элементарными.
Например: из простых высказываний

«Сергей футболист», «Сергей пловец» можно получить составное высказывание «Сергей футболист и пловец».

например: А, В, С.
Тогда если обозначить простые высказывания «Денис

сделал уроки» именем А, «Денис пошёл в кино» именем В, то составное высказывание «Денис сделал уроки и пошёл в кино» можно записать как «А и В». Здесь «и» -логическая связка, А, В - логические переменные, которые могут принимать логические значения «истина» или «ложь».

простых высказываний.
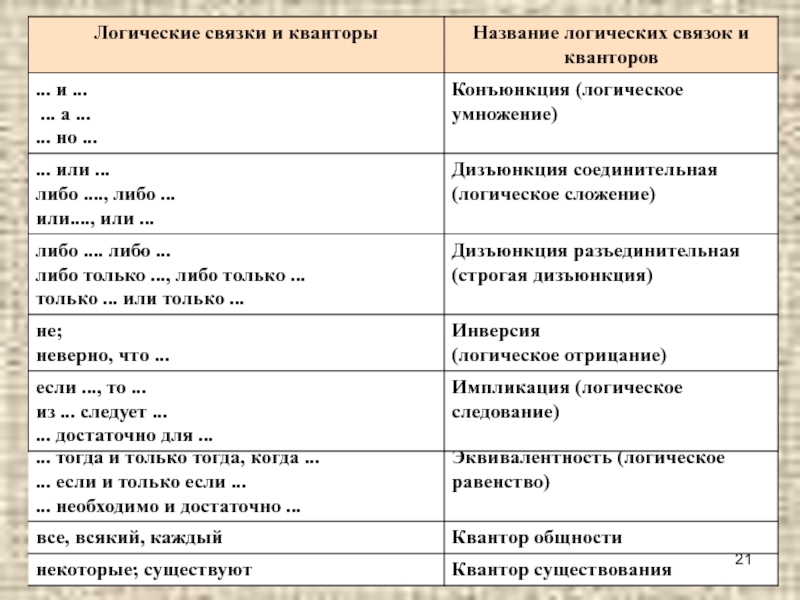
В алгебре логики логические связки рассматриваются как логические операции,

имеющие название и обозначение.

др. Информатика: ГИА: Учебно-справочные материалы для 9 класса – М.:

Просвещение, 2012.
Шауцукова Л. З. Информатика: Учеб. Пособие для общеобразоват. учреждений. – М.: Просвещение, 2010.


Источники иллюстраций:
Демокрит: http://www.help-rus-student.ru/text/22/708.htm
Евклид: http://im1-tub-ru.yandex.net/i?id=e816e4a3d4c6f191120f2d72c6ef9821-24-144&n=21
Декарт: http://im3-tub-ru.yandex.net/i?id=01efc70309e13263219738127be6b2c0-33-144&n=21
Аристотель: http://forexaw.com/TERMs/Ximiya/img178064_2-17_Aristotel.jpg
Ленйбниц: http://im3-tub-ru.yandex.net/i?id=c4a32acce10c0785f495be038826acfe-68-144&n=21
Дж. Буль: http://im2-tub-ru.yandex.net/i?id=e3383ccb5bb127862c43d96272b27319-59-144&n=21