Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Машина Тьюринга
Содержание
- 1. Машина Тьюринга
- 2. А́лан Мэ́тисон Тью́ринганглийский математик, логик, криптограф, оказавший
- 3. Машина Тьюринга это абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
- 4. Устройство машины Тьюринга В состав машины Тьюринга
- 5. 1. Внешний алфавит: А = {a0, a1, …,
- 6. 2. Внутренний алфавит Q = {q0, q1, …,
- 7. 3) Внешняя память (лента)Машина имеет ленту, разбитую
- 8. Художественное представление машины Тьюринга
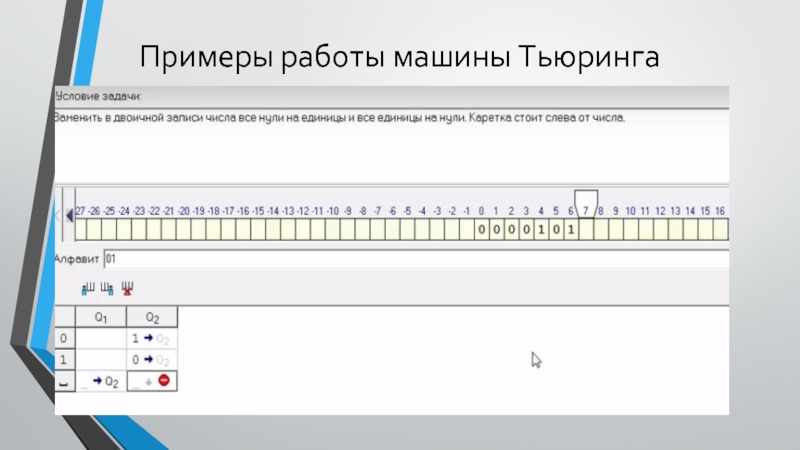
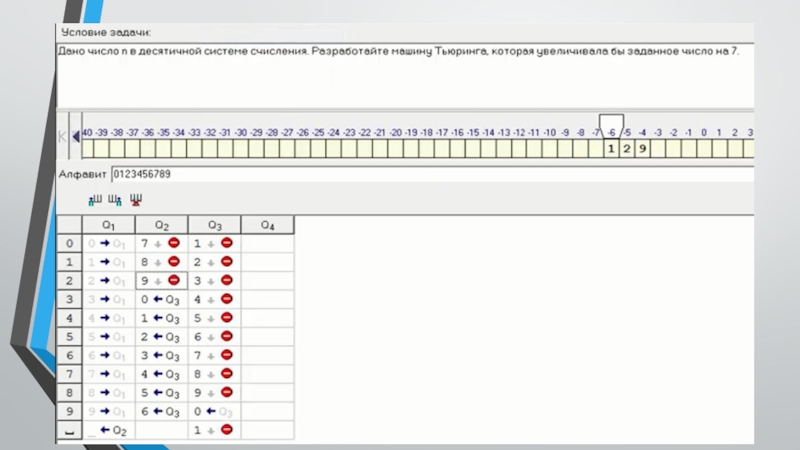
- 9. Примеры работы машины Тьюринга
- 10. Слайд 10
- 11. Можно сказать, что машина Тьюринга представляет собой
- 12. Скачать презентанцию
А́лан Мэ́тисон Тью́ринганглийский математик, логик, криптограф, оказавший существенное влияние на развитие информатики. Кавалер Ордена Британской империи , член Лондонского королевского общества . Предложенная им абстрактная вычислительная «Машина Тьюринга», которую можно считать
Слайды и текст этой презентации
Слайд 2
А́лан Мэ́тисон Тью́ринг
английский математик, логик, криптограф, оказавший существенное влияние на
Слайд 3
Машина Тьюринга это абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом
Тьюрингом в 1936 году для формализации понятия алгоритма.
Слайд 4Устройство машины Тьюринга
В состав машины Тьюринга входит неограниченная в обе
стороны лента, разделённая на ячейки, и управляющее устройство (также называется
головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Слайд 5
1. Внешний алфавит:
А = {a0, a1, …, a n}
Элемент a0
называется пустой символ.
В этом алфавите в виде слова
кодируется исходный набор данных и результат работы алгоритма Устройство машины Тьюринга.Слайд 6
2. Внутренний алфавит
Q = {q0, q1, …, qm}, {П, Л,
С}
В любой момент времени машина М находится в одном
из состояний q0, q1, …, qmСимволы {П, Л, С} – символы сдвига (вправо, влево, на месте)
Слайд 7
3) Внешняя память (лента)
Машина имеет ленту, разбитую на ячейки, в
каждую из которых может быть записана только одна буква.
Слайд 11
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину
с линейной памятью, которая согласно формальным правилам преобразует входные данные
с помощью последовательности элементарных действий. Несмотря на простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий.
Теги